5 voorbeelden van niet-lineaire relaties tussen variabelen

In de meeste statistiekcursussen leren studenten over lineaire relaties tussen variabelen.

Dit zijn relaties waarbij een toename van de ene variabele gepaard gaat met een voorspelbare toename van een andere variabele.

Een voorbeeld hiervan kan het aantal gespeelde minuten in een basketbalwedstrijd zijn, vergeleken met het totaal aantal gescoorde punten:

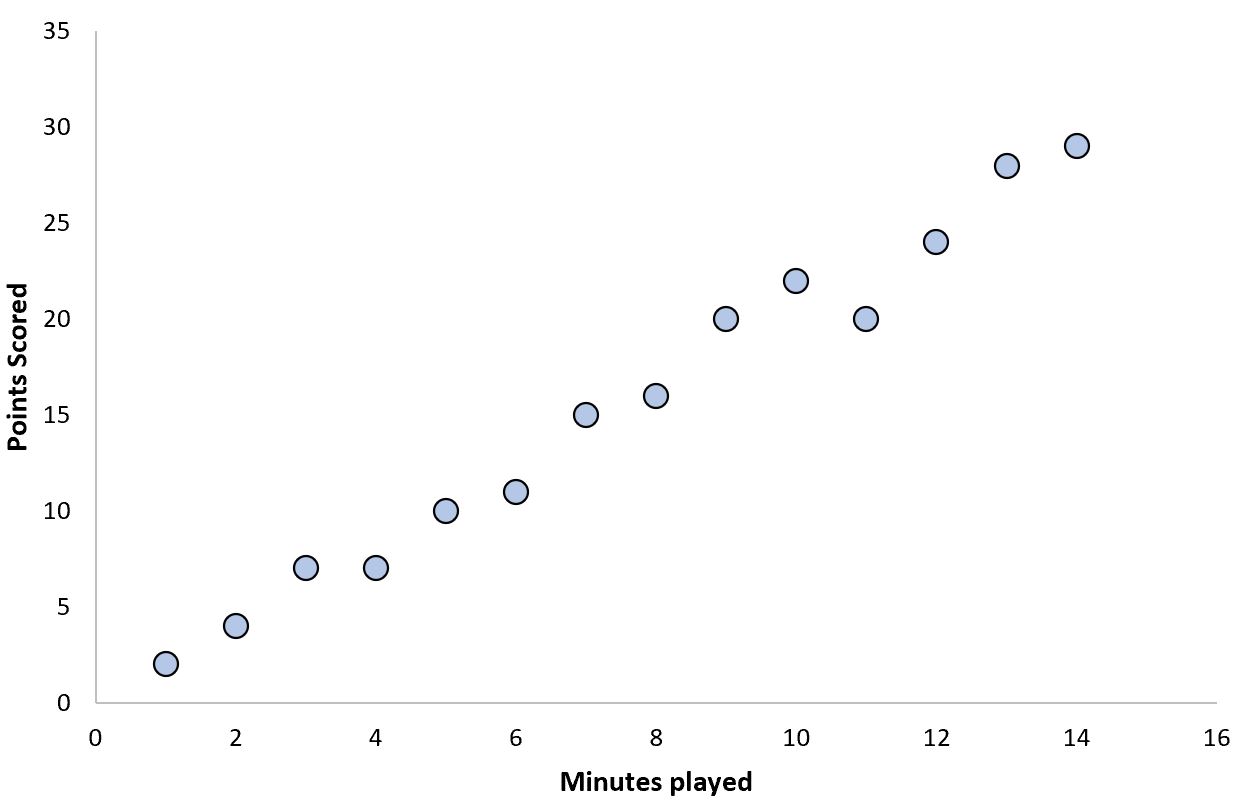
Spelers die meer minuten spelen, scoren doorgaans meer punten.

Er kunnen echter ook niet-lineaire relaties tussen variabelen bestaan, en deze verschijnen voortdurend in de echte wereld.

Deze tutorial biedt vijf voorbeelden van niet-lineaire relaties tussen variabelen in de echte wereld.

Voorbeeld 1: Kwadratische relaties

Een van de meest voorkomende niet-lineaire relaties in de echte wereld is de kwadratische relatie tussen variabelen.

Wanneer deze relatie in een spreidingsdiagram wordt uitgezet, heeft deze doorgaans de vorm van een „U“.

Een voorbeeld zou het totale aantal werkuren per week kunnen zijn, vergeleken met het algehele geluk:

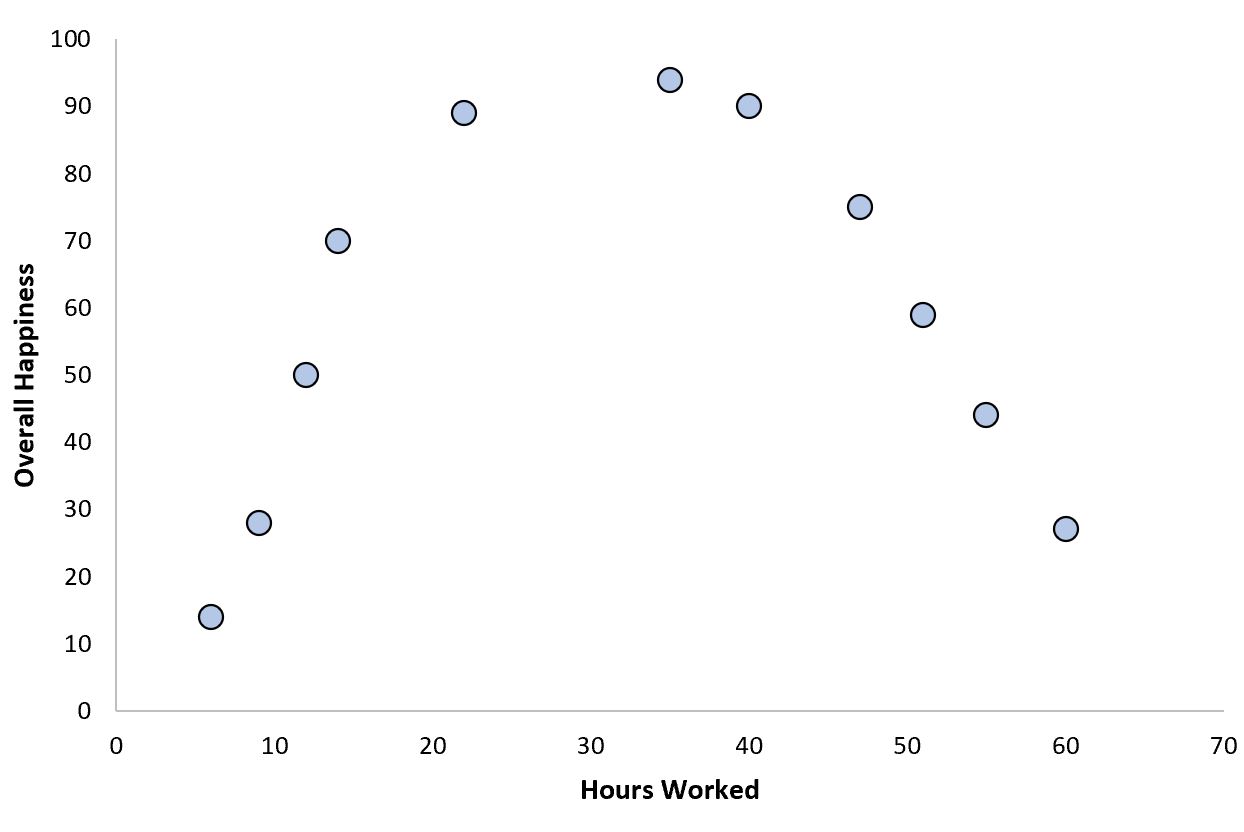
Naarmate de werkuren vanaf nul toenemen, neigt het algehele geluk toe te nemen, maar boven een bepaalde drempel leidt meer werkuren feitelijk tot een afname van het geluk.

Deze omgekeerde “U”-vorm is de karakteristieke vorm van een kwadratische relatie tussen twee variabelen.

Voorbeeld 2: Kubieke relaties

Een andere niet-lineaire relatie die in de echte wereld gebruikelijk is, is de kubieke relatie tussen variabelen.

Wanneer deze relatie in een spreidingsdiagram wordt uitgezet, vertoont deze doorgaans twee verschillende curven.

Dit soort relaties bestaat vaak tussen variabelen op het gebied van de thermodynamica:

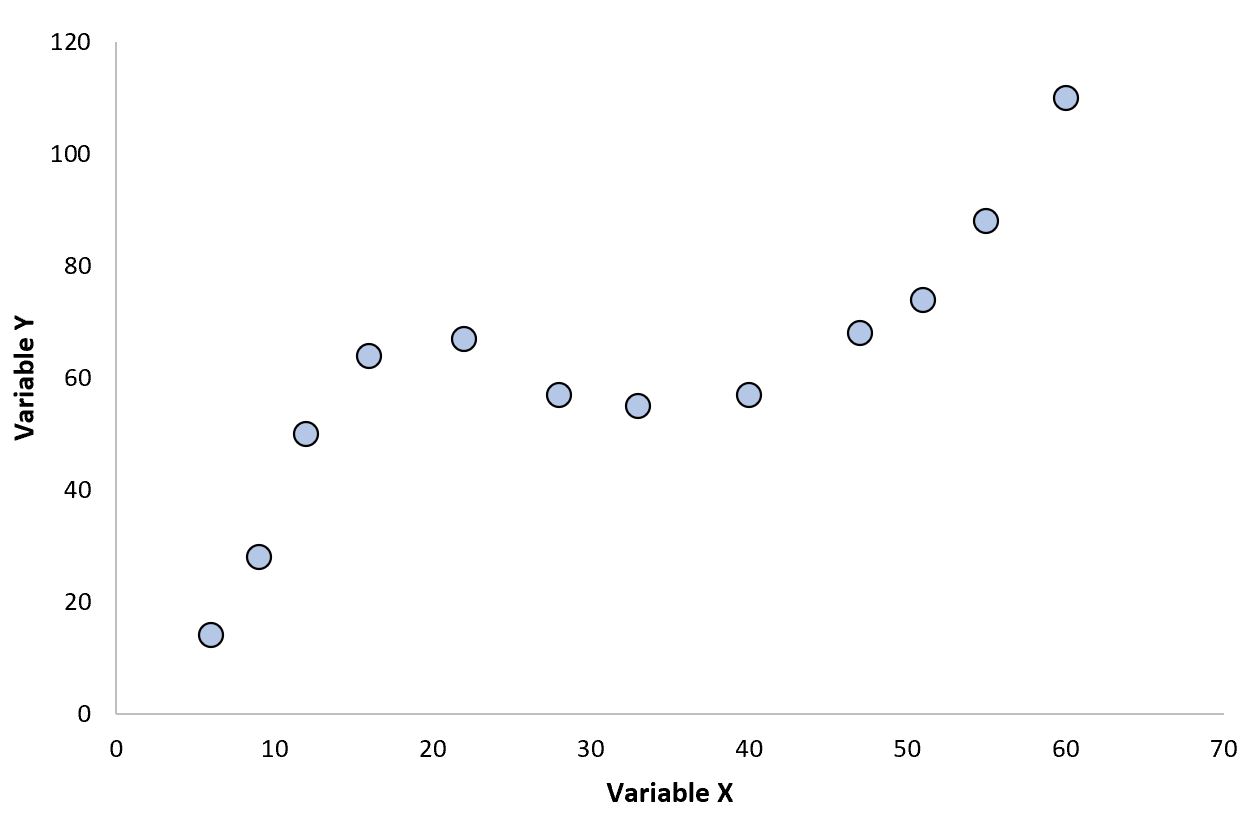
Merk op dat er twee verschillende curven in de grafiek voorkomen en dat de relatie tussen variabele X en variabele Y duidelijk niet lineair is.

Voorbeeld 3: Exponentiële relaties

Een andere niet-lineaire relatie die in de echte wereld gebruikelijk is, is de exponentiële relatie tussen variabelen.

Wanneer deze relatie in een spreidingsdiagram wordt uitgezet, vertoont deze een unieke curve die duidelijker wordt naarmate de variabele op de x-as toeneemt.

Een bekend voorbeeld van een exponentiële relatie is de levensduur van bamboeplanten en hun jaarlijkse groei:

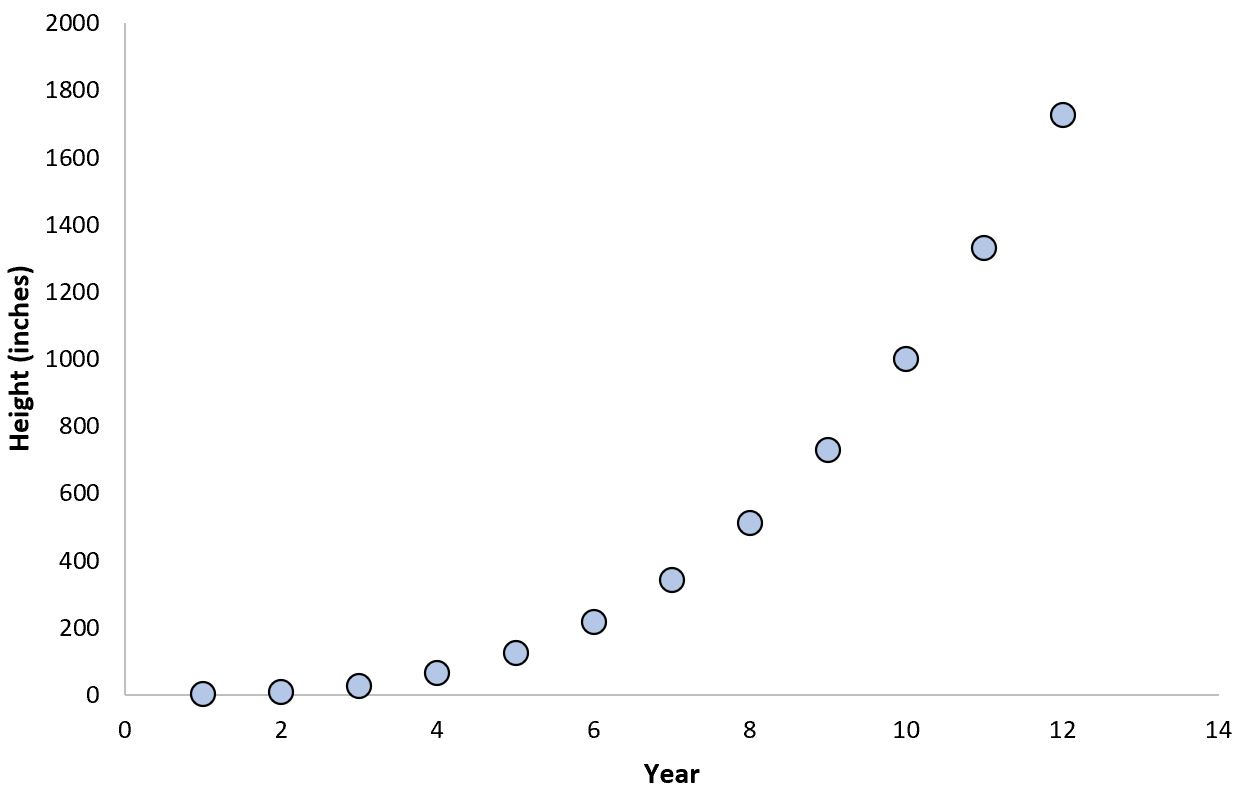
Tijdens de eerste paar jaar van de groei groeit een bamboeplant heel langzaam, maar zodra hij een bepaalde leeftijd bereikt, explodeert hij in hoogte en groeit hij snel.

Voorbeeld 4: Logaritmische relaties

Een andere niet-lineaire relatie die in de echte wereld gebruikelijk is, is de logaritmische relatie tussen variabelen.

Wanneer deze relatie in een spreidingsdiagram wordt uitgezet, vertoont deze een unieke curve die minder uitgesproken wordt naarmate de variabele op de x-as toeneemt.

Een voorbeeld van een logaritmische relatie is die tussen de efficiëntie van slimme thuistechnologieën en tijd:

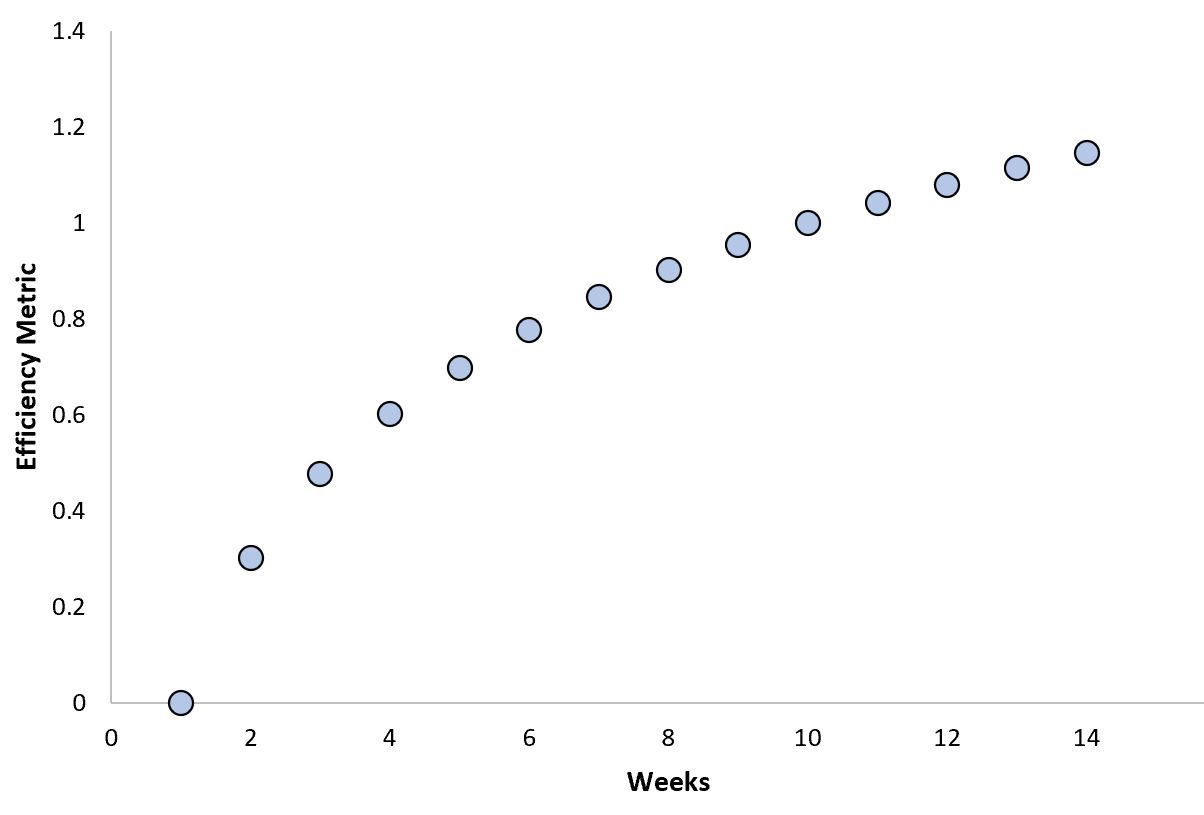
Wanneer nieuwe smart home-technologie (zoals een stofzuiger of zelfstandige airconditioner) in een huis wordt geïnstalleerd, leert het snel hoe het efficiënter kan worden, maar zodra het een bepaald punt bereikt, bereikt het een maximale drempel voor efficiëntie.

Voorbeeld 5: Cosinusrelaties

Een andere niet-lineaire relatie die in de echte wereld gebruikelijk is, is de cosinusrelatie tussen variabelen.

Wanneer deze relatie in een spreidingsdiagram wordt uitgezet, heeft deze de vorm van een “golf”.

Een voorbeeld van een cosinusrelatie is die tussen de frequentie van geluidsgolven en de tijd:

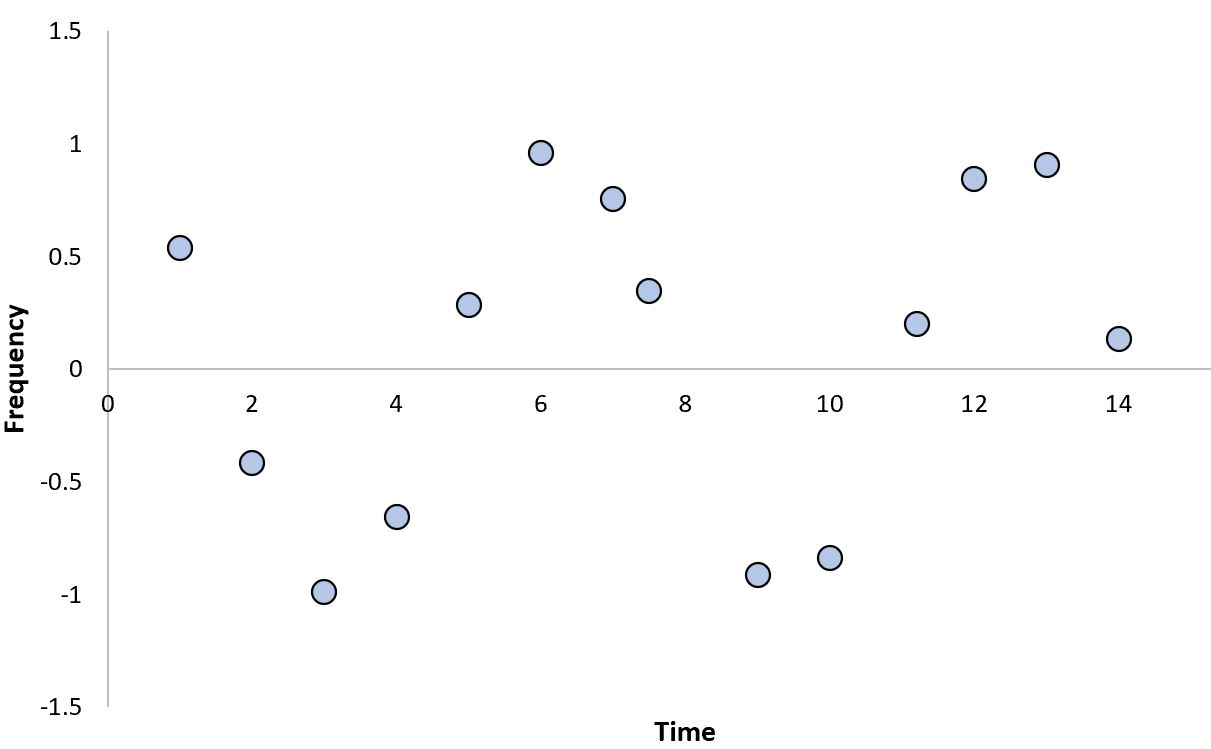
Merk op dat de relatie een ‘golfvorm’ heeft, die in hoge mate niet-lineair is.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u verschillende soorten niet-lineaire regressie in Excel kunt uitvoeren:

Hoe kwadratische regressie uit te voeren in Excel
Hoe kubieke regressie uit te voeren in Excel
Exponentiële regressie uitvoeren in Excel
Logaritmische regressie uitvoeren in Excel