Wat is een voorspellingsfout in de statistiek? (definitie & voorbeelden)
In de statistieken verwijst de voorspellingsfout naar het verschil tussen de waarden die door bepaalde modellen worden voorspeld en de werkelijke waarden.
Voorspellingsfouten worden vaak in twee contexten gebruikt:
1. Lineaire regressie: gebruikt om de waarde van een continue responsvariabele te voorspellen.
Normaal gesproken meten we de voorspellingsfout van een lineair regressiemodel met een metriek die bekend staat als RMSE , wat staat voor root mean square error.
Het wordt als volgt berekend:
RMSE = √ Σ(ŷ ik – y ik ) 2 / n
Goud:
- Σ is een symbool dat “som” betekent
- ŷ i is de voorspelde waarde voor de i- de waarneming
- y i is de waargenomen waarde voor de i-de waarneming
- n is de steekproefomvang
2. Logistische regressie: gebruikt om de waarde van een binaire responsvariabele te voorspellen.
Een gebruikelijke manier om de voorspellingsfout van een logistisch regressiemodel te meten, is door een metriek te gebruiken die bekend staat als het totale classificatiefoutenpercentage.
Het wordt als volgt berekend:
Totaal aantal misclassificaties = (# onjuiste voorspellingen / # totale voorspellingen)
Hoe lager de waarde van het misclassificatiepercentage, hoe beter het model de resultaten van de responsvariabele kan voorspellen.
De volgende voorbeelden laten zien hoe u in de praktijk de voorspellingsfout voor een lineair regressiemodel en een logistisch regressiemodel kunt berekenen.
Voorbeeld 1: Berekening van de voorspellingsfout bij lineaire regressie
Stel dat we een regressiemodel gebruiken om te voorspellen hoeveel punten 10 spelers zullen scoren in een basketbalwedstrijd.
De volgende tabel toont de door het model voorspelde punten, vergeleken met de daadwerkelijke punten die door de spelers zijn gescoord:
We zouden de root mean square error (RMSE) als volgt berekenen:
- RMSE = √ Σ(ŷ ik – y ik ) 2 / n
- RMSE = √(((14-12) 2 +(15-15) 2 +(18-20) 2 +(19-16) 2 +(25-20) 2 +(18-19) 2 +(12- 16) 2 +(12-20) 2 +(15-16) 2 +(22-16) 2 ) / 10)
- RMSE = 4
De gemiddelde kwadratische fout is 4. Dit vertelt ons dat de gemiddelde afwijking tussen de voorspelde gescoorde punten en de daadwerkelijk gescoorde punten 4 is.
Gerelateerd: Wat wordt beschouwd als een goede RMSE-waarde?
Voorbeeld 2: Berekening van de voorspellingsfout bij logistische regressie
Stel dat we een logistisch regressiemodel gebruiken om te voorspellen of tien universiteitsbasketbalspelers wel of niet zullen worden opgeroepen voor de NBA.
De volgende tabel toont de voorspelde uitkomst voor elke speler versus de werkelijke uitkomst (1 = opgesteld, 0 = niet opgesteld):
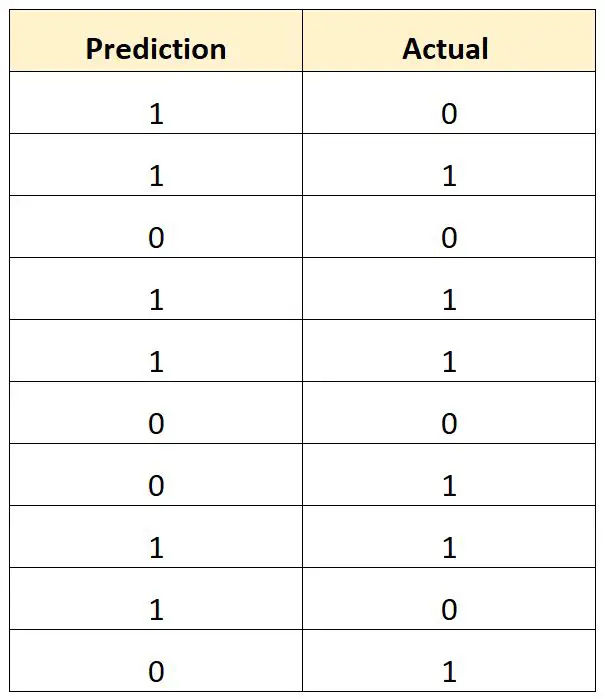
We berekenen het totale percentage misclassificaties als volgt:
- Totaal aantal misclassificaties = (# onjuiste voorspellingen / # totale voorspellingen)
- Totaal classificatiefoutenpercentage = 4/10
- Totaal percentage misclassificaties = 40%
Het totale classificatiefoutenpercentage bedraagt 40% .
Deze waarde is vrij hoog, wat aangeeft dat het model niet zo goed kan voorspellen of een speler wordt opgeroepen of niet.
Aanvullende bronnen
De volgende tutorials bieden een inleiding tot de verschillende soorten regressiemethoden:
Inleiding tot eenvoudige lineaire regressie
Inleiding tot meervoudige lineaire regressie
Inleiding tot logistieke regressie
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder