Voorwaardelijke waarschijnlijkheid (of voorwaardelijke waarschijnlijkheid)

Hier kom je te weten wat voorwaardelijke waarschijnlijkheid (of voorwaardelijke waarschijnlijkheid) is. We leggen uit hoe voorwaardelijke waarschijnlijkheid wordt berekend met een voorbeeld en de eigenschappen van dit type waarschijnlijkheid. Daarnaast kun je oefenen met stapsgewijs opgeloste voorwaardelijke waarschijnlijkheidsoefeningen.

Wat is voorwaardelijke waarschijnlijkheid?

Voorwaardelijke waarschijnlijkheid , ook wel voorwaardelijke waarschijnlijkheid genoemd, is een statistische maatstaf die de waarschijnlijkheid aangeeft dat gebeurtenis A zal plaatsvinden als een andere gebeurtenis B plaatsvindt. Dat wil zeggen dat de voorwaardelijke waarschijnlijkheid P(A|B) verwijst naar de waarschijnlijkheid dat gebeurtenis A plaatsvindt nadat gebeurtenis B al heeft plaatsgevonden.

Voorwaardelijke waarschijnlijkheid wordt geschreven met een verticale balk tussen de twee gebeurtenissen: P(A|B), en luidt: “de voorwaardelijke waarschijnlijkheid van gebeurtenis A gegeven gebeurtenis B”.

Houd er rekening mee dat de voorwaardelijke waarschijnlijkheidswaarde een getal tussen 0 en 1 is. Hoe hoger de voorwaardelijke waarschijnlijkheid, hoe waarschijnlijker het is dat gebeurtenis A zal plaatsvinden wanneer gebeurtenis B plaatsvindt, maar hoe lager de voorwaardelijke waarschijnlijkheid, hoe kleiner de kans dat gebeurtenis A plaatsvindt. zal plaatsvinden wanneer gebeurtenis B plaatsvindt.

Voorwaardelijke waarschijnlijkheidsformule

De voorwaardelijke waarschijnlijkheid van gebeurtenis A bij gegeven gebeurtenis B is gelijk aan de waarschijnlijkheid van het snijpunt tussen gebeurtenis A en gebeurtenis B gedeeld door de waarschijnlijkheid van gebeurtenis B.

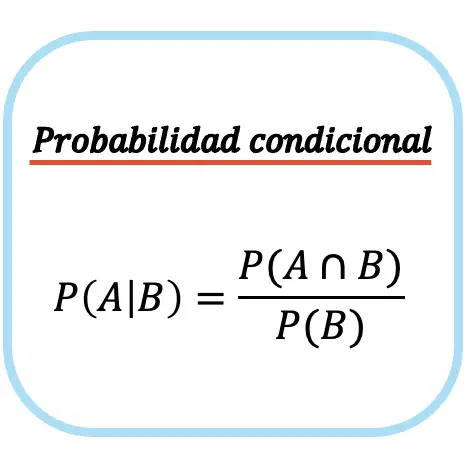
Merk op dat de formule voor voorwaardelijke waarschijnlijkheid (of voorwaardelijke waarschijnlijkheid) alleen kan worden gebruikt als de waarschijnlijkheid van het optreden van de ongeconditioneerde gebeurtenis niet nul is, dwz P(B)≠0. Of met andere woorden: of het mogelijk is dat gebeurtenis B plaatsvindt.

De voorwaardelijke waarschijnlijkheid kan ook worden berekend op basis van de inverse ervan, dwz als P(B|A) bekend is, kan P(A|B) worden bepaald. Maar om dit te doen moet je de stelling van Bayes toepassen, je kunt hier zien waaruit deze stelling bestaat:

Voorbeeld van voorwaardelijke waarschijnlijkheid

Zodra we hebben gezien wat de definitie en formule van voorwaardelijke waarschijnlijkheid is, zullen we stap voor stap een voorbeeld van dit type waarschijnlijkheid oplossen om de betekenis ervan volledig te begrijpen.

• Na het afleggen van een examen in een klas van 30 studenten werden gegevens verzameld om te achterhalen hoeveel studenten hebben gestudeerd en hoeveel geslaagd. De resultaten worden weergegeven in de volgende kruistabel. Bereken uit de verzamelde gegevens de voorwaardelijke kans om voor een examen te slagen als je al hebt gestudeerd.

Om de voorwaardelijke waarschijnlijkheid te verkrijgen, moeten we de formule toepassen die we eerder zagen:

Daarom moeten we eerst de waarschijnlijkheid vinden dat een student heeft gestudeerd en gestudeerd en geslaagd. Om de waarschijnlijkheid te bepalen dat een student heeft gestudeerd, hoeven we alleen maar de regel van Laplace te gebruiken, dat wil zeggen: we delen het aantal studenten dat heeft gestudeerd door het totale aantal observaties:

En we kunnen uit de kruistabel de waarschijnlijkheid achterhalen dat een student tegelijkertijd heeft gestudeerd en geslaagd door het aantal studenten dat heeft gestudeerd en geslaagd te delen door het totaal:

De kans dat een student slaagt voor een examen als hij gestudeerd heeft, is dus:

Voorwaardelijke waarschijnlijkheid van afhankelijke en onafhankelijke gebeurtenissen

In deze paragraaf zullen we zien wat de relatie is tussen voorwaardelijke waarschijnlijkheid en afhankelijke en onafhankelijke gebeurtenissen (of afhankelijke en onafhankelijke gebeurtenissen). Omdat deze twee soorten gebeurtenissen, hoewel het verschillende concepten zijn, gekoppeld zijn aan een voorwaardelijke waarschijnlijkheid.

Twee gebeurtenissen (of gebeurtenissen) zijn onafhankelijk als de waarschijnlijkheid van optreden niet van elkaar afhankelijk is. In een dergelijk geval is het snijpunt tussen de twee gebeurtenissen gelijk aan het product van de waarschijnlijkheid van elke gebeurtenis afzonderlijk. En daarom is de voorwaardelijke waarschijnlijkheidsformule vereenvoudigd:

Kortom, als gebeurtenissen A en B onafhankelijk zijn, is de voorwaardelijke waarschijnlijkheid van gebeurtenis A gegeven gebeurtenis B precies gelijk aan de waarschijnlijkheid dat gebeurtenis A plaatsvindt.

Aan de andere kant, wanneer twee gebeurtenissen afhankelijk zijn, betekent dit dat de waarschijnlijkheid van de ene gebeurtenis afhangt van de waarschijnlijkheid van de andere gebeurtenis. Wanneer twee gebeurtenissen A en B afhankelijk zijn, is de voorwaardelijke waarschijnlijkheid van gebeurtenis A bij een gegeven gebeurtenis B dus verschillend van de waarschijnlijkheid dat gebeurtenis A plaatsvindt.

Opgeloste voorwaardelijke waarschijnlijkheidsoefeningen

Oefening 1

We weten dat in een zak vol ballen de helft oranje is en de andere helft groen. Bovendien is een derde van alle ballen oranje en tegelijkertijd gemarkeerd met een teken. Wat is de kans dat wanneer je een oranje bal trekt, deze het signaal ontvangt?

Om de oefening op te lossen, moeten we de voorwaardelijke waarschijnlijkheidsformule toepassen, namelijk:

De probleemstelling vertelt ons dat de helft van de zak uit sinaasappelen bestaat. Daarom is de theoretische kans dat je een oranje bal oppakt 50%.

Aan de andere kant weten we dat een derde van het totaal oranje ballen zijn en een signaal hebben, dus de kans op het verkrijgen van een oranje bal met een signaal is:

Ten slotte vervangen we de berekende kansen in de voorwaardelijke waarschijnlijkheidsformule om de waarde ervan te vinden:

Samenvattend is de kans op het trekken van een bal met het signaal als deze oranje is 66%.

Oefening 2

Als we zes blauwe pennen en drie zwarte pennen in een doos hebben, bereken dan de kans dat we één blauwe pen trekken en de kans dat we twee blauwe pennen achter elkaar trekken.

Om de waarschijnlijkheid te bepalen dat je ooit een blauwe pen oppakt, gebruik je eenvoudigweg de wet van Laplace:

Het probleem vraagt ons ook om de waarschijnlijkheid te kennen dat we twee blauwe pennen achter elkaar oppakken, dat wil zeggen de voorwaardelijke waarschijnlijkheid dat we een blauwe pen oppakken als we al eerder een blauwe pen hebben opgepakt.

Als we een blauwe pen trekken, hebben we een minder gunstig geval, maar er is ook één pen minder in het totaal. De voorwaardelijke waarschijnlijkheid is daarom:

Oefening 3

Wat is de voorwaardelijke kans dat een dobbelsteen naar nummer 4 wordt gegooid, gegeven het feit dat een toss kop oplevert?

Om deze oefening op te lossen, moet je rekening houden met de theorie van de voorwaardelijke waarschijnlijkheid, omdat de gebeurtenissen ‘het getal 4 krijgen door een dobbelsteen te gooien’ en ‘kop krijgen door een munt op te gooien’ onafhankelijk zijn. Het is daarom niet nodig om de voorwaardelijke waarschijnlijkheidsformule te gebruiken, maar er wordt voldaan aan de volgende gelijkheid:

Om de voorwaardelijke waarschijnlijkheid te vinden, gebruikt u eenvoudigweg de regel van Laplace:

Oefening 4

Van 25 bedrijven in een land werd het boekjaar bestudeerd en hoe hun aandelenkoersen veranderen afhankelijk van het economische resultaat van dat jaar. U kunt de verzamelde gegevens bekijken in de volgende kruistabel:

Hoe waarschijnlijk is het dat de aandelenkoers van een bedrijf zal stijgen als het het afgelopen jaar winst heeft gemaakt?

De oefening vraagt ons naar de voorwaardelijke waarschijnlijkheid dat de aandelen zullen stijgen, gegeven het feit dat het bedrijf een positief economisch resultaat heeft behaald. Om deze waarschijnlijkheid te berekenen, moeten we dus de voorwaardelijke waarschijnlijkheidsformule gebruiken:

We berekenen daarom eerst de kans dat een bedrijf winst maakt en vervolgens de kans dat een bedrijf economische winst maakt terwijl de prijs per aandeel stijgt:

En dan vervangen we de gevonden waarden in de formule en berekenen we de voorwaardelijke waarschijnlijkheid:

Eigenschappen van voorwaardelijke waarschijnlijkheid

De eigenschappen van voorwaardelijke waarschijnlijkheid, of voorwaardelijke waarschijnlijkheid, zijn als volgt:

• De som van de voorwaardelijke waarschijnlijkheid van gebeurtenis A, gegeven gebeurtenis B, plus de voorwaardelijke waarschijnlijkheid van de complementaire gebeurtenis A, gegeven gebeurtenis B, is gelijk aan één.

• Als gebeurtenis A een deelverzameling is van gebeurtenis B, zal A altijd plaatsvinden als B waar is. De voorwaardelijke waarschijnlijkheid van gebeurtenis A gegeven gebeurtenis B is in deze gevallen dus 1.

• Gegeven twee verschillende gebeurtenissen geldt altijd de volgende gelijkheid met betrekking tot de voorwaardelijke waarschijnlijkheid: