Waarom is standaarddeviatie belangrijk? (uitleg + voorbeelden)

De standaarddeviatie wordt gebruikt om de verdeling van waarden in een steekproef te meten.

We kunnen de volgende formule gebruiken om de standaardafwijking van een bepaald monster te berekenen:

√ Σ(x _i – x _bar ) ² / (n-1)

Goud:

• Σ: Een symbool dat “som” betekent
• x _i : de ^i- de waarde van het monster
• x _bar : Het monster betekent
• n: De steekproefomvang

Hoe hoger de standaarddeviatiewaarde, hoe meer verspreid de waarden in een steekproef zijn. Omgekeerd geldt: hoe lager de standaardafwijkingswaarde, hoe nauwer de waarden geclusterd zijn.

Een vraag die studenten vaak stellen is: waarom is de standaarddeviatie belangrijk?

Het antwoord: standaarddeviatie is belangrijk omdat het ons de verdeling van waarden in een bepaalde dataset vertelt.

we analyseren een dataset Wanneer we de volgende statistieken willen vinden:

• Het centrum van de gegevensset . De meest gebruikelijke manier om ‚centrum‘ te meten is door het gemiddelde en de mediaan te gebruiken.
• De verdeling van waarden in de dataset . De meest gebruikelijke manier om de spreiding te meten is door gebruik te maken van de standaarddeviatie.

Door te weten waar het centrum ligt en wat de verdeling van waarden is, kunnen we de verdeling van waarden in elke dataset goed begrijpen.

De volgende voorbeelden illustreren het belang van standaarddeviatie in de praktijk.

Voorbeeld 1: Salarisverdeling

Stel dat het gemiddelde salaris bij bedrijf A €80.000 is en de standaardafwijking €20.000. Omdat de standaardafwijking zo groot is, is er geen garantie dat u bijna €80.000 per jaar betaald krijgt als u bij dit bedrijf werkt, omdat er zoveel variatie in salarissen is.

Omgekeerd: stel dat het gemiddelde salaris bij bedrijf B ook €80.000 bedraagt, maar dat de standaardafwijking slechts €4.000 bedraagt. Omdat deze standaardafwijking zo klein is, kunt u er zeker van zijn dat u bijna €80.000,- betaald krijgt, omdat er zeer weinig variatie in salarissen is.

Als we een boxplot zouden maken om de salarisverdeling bij deze twee bedrijven te visualiseren, zou het er als volgt uit kunnen zien:

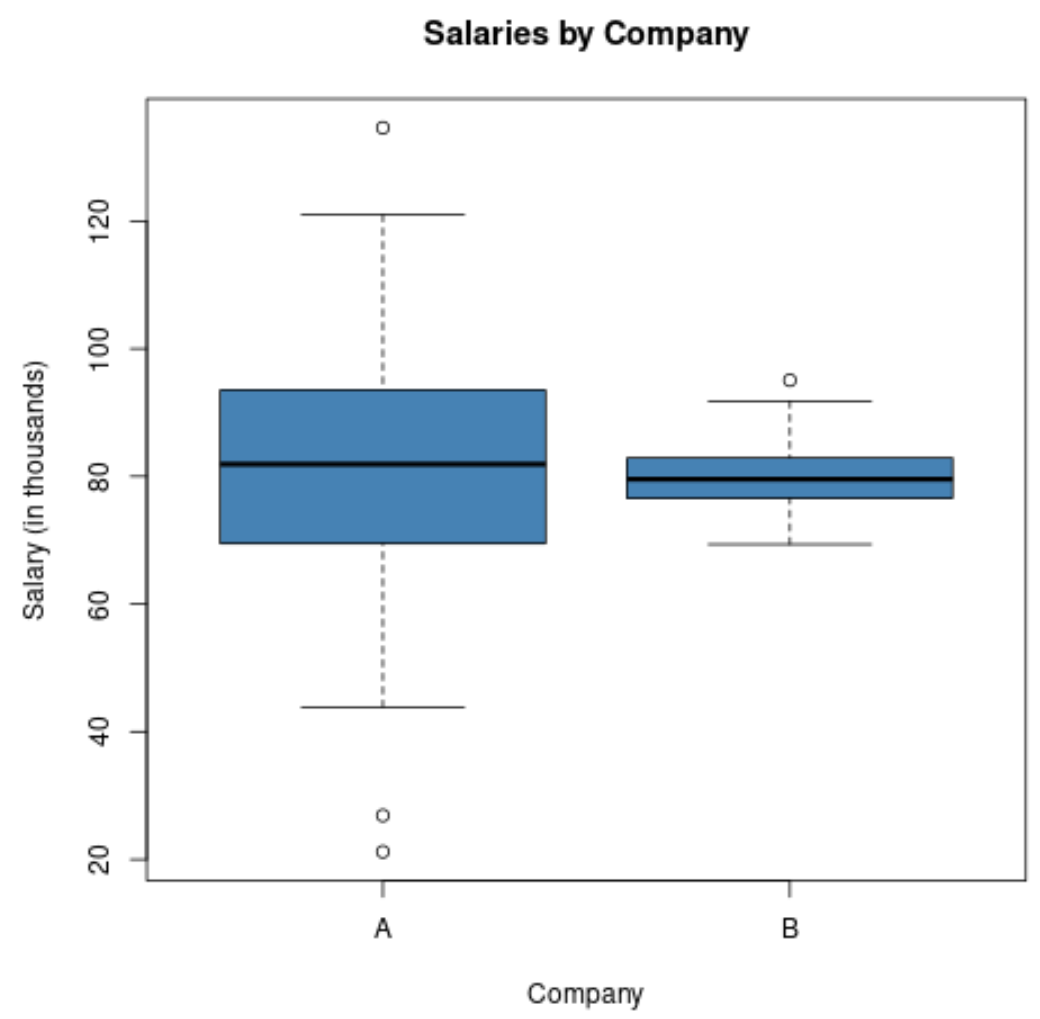
Merk op dat de lengte van de boxplot voor bedrijf A groter is naarmate de standaarddeviatie van de lonen veel hoger is.

Beide bedrijven hebben hetzelfde gemiddelde salaris, maar de salariskloof is veel groter in bedrijf A.

Voorbeeld 2: Verdeling van de huizenprijzen

Stel dat de gemiddelde huizenprijs in buurt A €250.000 bedraagt en de standaarddeviatie €50.000. Omdat de standaardafwijking vrij groot is, betekent dit dat sommige huizenprijzen veel hoger zullen zijn dan $250.000, en andere veel lager. Als je naar een bepaald huis in deze buurt kijkt, is er geen garantie dat de prijs ergens in de buurt van het gemiddelde zal liggen.

Omgekeerd: stel dat de gemiddelde huizenprijs in buurt B ook $250.000 bedraagt, maar de standaarddeviatie bedraagt slechts $10.000. Omdat deze standaardafwijking vrij klein is, kunt u er zeker van zijn dat elk huis dat u in de buurt bekijkt waarschijnlijk voor deze prijs gesloten zal zijn.

Als we een boxplot zouden maken om de verdeling van de huizenprijzen in deze twee buurten te visualiseren, zou het er als volgt uit kunnen zien:

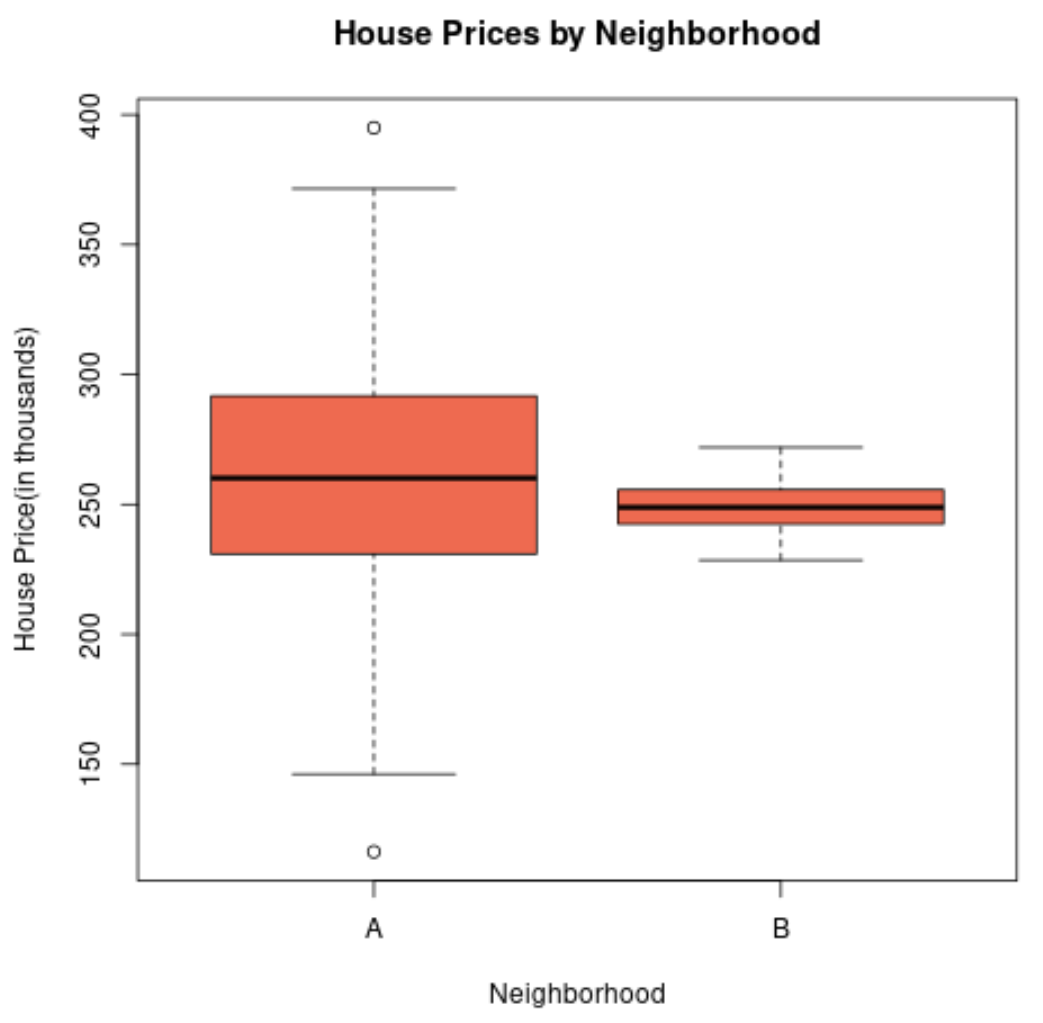
De lengte van de boxplot van wijk A is groter naarmate de standaardafwijking van de vastgoedprijzen veel hoger is.

In feite variëren de huizenprijzen van minder dan $150.000 tot meer dan $400.000 voor buurt A, terwijl de prijzen voor buurt B slechts variëren van ongeveer $230.000 tot $270.000.

Door eenvoudigweg de standaardafwijking van de huizenprijzen in elke buurt te kennen, kunnen we weten hoeveel variatie we in de prijzen in elke buurt kunnen verwachten.

Aanvullende bronnen

Wat wordt als een goede standaarddeviatie beschouwd?
Bereik versus Standaardafwijking: wanneer moet u ze gebruiken?
Variatiecoëfficiënt versus standaardafwijking: het verschil