Waarschijnlijkheid van kruispunt van gebeurtenissen

In dit artikel wordt uitgelegd hoe u de waarschijnlijkheid van het kruispunt van gebeurtenissen kunt berekenen. Je zult dus ontdekken wat de formule is voor de waarschijnlijkheid van het kruisen van gebeurtenissen en bovendien oefeningen die stap voor stap worden opgelost.

Wat is het kruispunt van gebeurtenissen?

In de waarschijnlijkheidstheorie is het snijpunt van gebeurtenissen een operatie van gebeurtenissen waarvan het resultaat is samengesteld uit elementaire gebeurtenissen die alle gebeurtenissen van de operatie gemeen hebben. Dat wil zeggen dat het snijpunt van gebeurtenissen A en B wordt gevormd door alle gebeurtenissen die tegelijkertijd tot A en B behoren.

Het snijpunt van twee gebeurtenissen wordt uitgedrukt door het symbool ⋂. Het snijpunt van gebeurtenissen A en B wordt dus geschreven als A⋂B.

Als er in het willekeurige experiment van het gooien van een dobbelsteen bijvoorbeeld een even getal wordt gegooid A={2, 4, 6} en een andere gebeurtenis is dat een getal groter dan drie wordt gegooid, B={4, 5, 6 }, het snijpunt van de twee gebeurtenissen is A⋂B={4, 6}.

Formule voor de waarschijnlijkheid van het kruisen van gebeurtenissen

De waarschijnlijkheid dat twee gebeurtenissen elkaar kruisen, is gelijk aan de waarschijnlijkheid dat één gebeurtenis plaatsvindt maal de voorwaardelijke waarschijnlijkheid dat de andere gebeurtenis plaatsvindt, gegeven de eerste gebeurtenis.

Daarom is de formule voor de waarschijnlijkheid van het snijpunt van twee gebeurtenissen P(A⋂B)=P(A) P(B|A)=P(B) P(A|B).

Goud:

• 

  En

  

  Dit zijn twee afhankelijke gebeurtenissen.

• 

  is de waarschijnlijkheid van het snijpunt van gebeurtenis A en gebeurtenis B.

• 

  is de waarschijnlijkheid dat gebeurtenis A zal plaatsvinden.

• 

  is de voorwaardelijke waarschijnlijkheid dat gebeurtenis B plaatsvindt, gegeven gebeurtenis A.

• 

  is de waarschijnlijkheid dat gebeurtenis B zal plaatsvinden.

• 

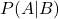
  is de voorwaardelijke waarschijnlijkheid dat gebeurtenis A plaatsvindt, gegeven gebeurtenis B.

Als de twee gebeurtenissen echter onafhankelijk zijn, betekent dit dat de waarschijnlijkheid dat de ene gebeurtenis plaatsvindt, niet afhangt van het feit of de andere gebeurtenis plaatsvindt. Daarom is de formule voor de waarschijnlijkheid van het kruisen van de twee onafhankelijke gebeurtenissen als volgt:

Goud:

• 

  En

  

  Dit zijn twee onafhankelijke gebeurtenissen.

• 

  is de waarschijnlijkheid van het snijpunt van gebeurtenis gebeurtenis A en gebeurtenis B.

• 

  is de waarschijnlijkheid dat gebeurtenis A zal plaatsvinden.

• 

  is de waarschijnlijkheid dat gebeurtenis B zal plaatsvinden.

Voorbeelden uit de praktijk van de waarschijnlijkheid van kruispunten van gebeurtenissen

Vervolgens laten we u twee voorbeelden stap voor stap oplossen, zodat u kunt zien hoe de waarschijnlijkheid van het kruisen van twee gebeurtenissen wordt berekend. We zullen eerst een voorbeeld zien van de kruising van twee onafhankelijke gebeurtenissen en vervolgens twee afhankelijke gebeurtenissen, zodat u beide gevallen kunt zien.

Waarschijnlijkheid van de kruising van twee onafhankelijke gebeurtenissen

• Er wordt drie keer op rij een trekking gelanceerd. Bereken de kans dat je kop krijgt bij alle drie de worpen.

In dit geval zijn de gebeurtenissen waarvoor we de gezamenlijke waarschijnlijkheid willen berekenen onafhankelijk, aangezien het resultaat van een trekking niet afhankelijk is van het resultaat verkregen bij de vorige trekking. Om de waarschijnlijkheid te bepalen dat we drie opeenvolgende kop krijgen, moeten we daarom de formule voor de snijkans voor onafhankelijke gebeurtenissen gebruiken:

Bij lottrekking zijn er slechts twee mogelijke resultaten: we kunnen kop of munt krijgen. Daarom is de kans op kop of munt bij het opgooien van een munt:

Om dus de kans te vinden dat we kop krijgen bij alle drie de muntopgooien, moeten we de kans op kop met drie vermenigvuldigen:

Kortom, de kans dat je drie keer op rij kop krijgt is 12,5%.

Waarschijnlijkheid van de kruising van twee afhankelijke gebeurtenissen

• In een lege doos stoppen we 8 blauwe ballen, 4 oranje ballen en 2 groene ballen. Als we eerst één bal trekken en dan nog een bal, zonder de eerste teruggetrokken bal terug in de doos te leggen, wat is dan de kans dat de eerste bal blauw is en de tweede bal oranje?

In dit geval zijn de gebeurtenissen afhankelijk, omdat de kans op het oppakken van een oranje bal bij de tweede trekking afhangt van de kleur van de getrokken bal bij de eerste trekking. Om de waarschijnlijkheid te berekenen die het probleem ons vraagt, moeten we daarom de formule gebruiken voor de snijkans voor afhankelijke gebeurtenissen:

De kans op het verkrijgen van een blauwe bal bij de eerste trekking is eenvoudig te bepalen, deel simpelweg het aantal blauwe ballen door het totale aantal ballen:

Aan de andere kant wordt de kans op het trekken van een oranje bal na het nemen van een blauwe bal anders berekend omdat het aantal oranje ballen anders is en bovendien er nu één bal minder in de doos ligt:

De kans dat je eerst een blauwe bal trekt en vervolgens een oranje bal, wordt dus berekend door de twee hierboven gevonden kansen te vermenigvuldigen:

Eigenschappen van gebeurteniskruispunten

In de waarschijnlijkheidstheorie heeft het snijpunt van gebeurtenissen de volgende eigenschappen:

• Commutatieve eigenschap: de volgorde van kruispuntgebeurtenissen verandert het resultaat van de bewerking niet.

• Associatieve eigenschap: Het snijpunt van drie gebeurtenissen kan in elke volgorde worden berekend, omdat het resultaat hetzelfde is.

• Distributieve eigenschap: de kruising van gebeurtenissen voldoet aan de distributieve eigenschap bij de vereniging van gebeurtenissen.