Hoe u de waarschijnlijkheid van minstens één kop kunt bepalen bij het opgooien van munten

Bij een bepaalde toss is de kans op kop 1/2 of 0,5.

Om de kans te bepalen dat je bij een bepaald aantal opgooien minstens één kop krijgt, kun je de volgende formule gebruiken:

P(Minstens één kop) = 1 – 0,5 ⁿ

Goud:

• n : Totaal aantal omkeringen

Stel dat we bijvoorbeeld twee keer een munt opgooien.

De kans om tijdens deze 3 worpen minstens één kop te krijgen is:

• P(Minstens één kop) = 1 – 0,5 ⁿ
• P(Minstens één kop) = 1 – 0,5 ³
• P (minstens één kop) = 1 – 0,125
• P(ten minste één kop) = 0,875

Dit antwoord is logisch als we alle mogelijke uitkomsten voor twee keer opgooien van een munt opsommen, waarbij “T” staat voor kop en “H” voor munt:

• TTT
• TTH
• THH
• THT
• HHHH
• VRD
• HTH
• HTT

Merk op dat ten minste één hoofd (H) voorkomt in 7 van de 8 mogelijke uitkomsten, wat neerkomt op 7/8 = 0,875 .

Of stel dat we vijf keer een munt opgooien.

De kans om tijdens deze 5 worpen minstens één kop te krijgen is:

• P(Minstens één kop) = 1 – 0,5 ⁿ
• P(Minstens één kop) = 1 – 0,5 ⁵
• P(tenminste één hoofd) = 1 – 0,25
• P(ten minste één kop) = 0,96875

De volgende tabel toont de kans op het krijgen van minstens één kop tijdens verschillende aantallen opgooien:

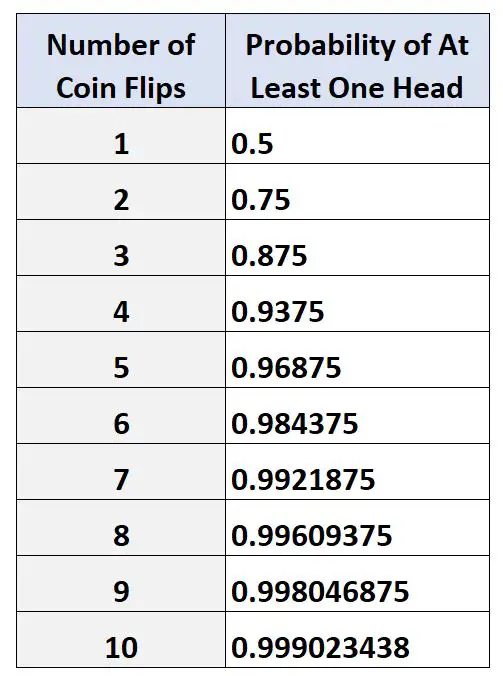
Houd er rekening mee dat hoe hoger het aantal opgooien van munten, hoe groter de kans is dat u minstens één kop krijgt.

Dit zou logisch moeten zijn, aangezien we een grotere kans zouden moeten hebben om uiteindelijk een hoofd te zien verschijnen als we de munt meerdere keren blijven opgooien.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere algemene waarschijnlijkheidsgerelateerde berekeningen kunt uitvoeren:

Hoe u de waarschijnlijkheid van “minstens één” succes kunt bepalen
Hoe u de waarschijnlijkheid van „minstens twee“ successen kunt vinden
Hoe de waarschijnlijkheid van A en B te vinden
Hoe de waarschijnlijkheid van A of B te vinden