Waarschijnlijkheid vs. proportie: wat is het verschil?

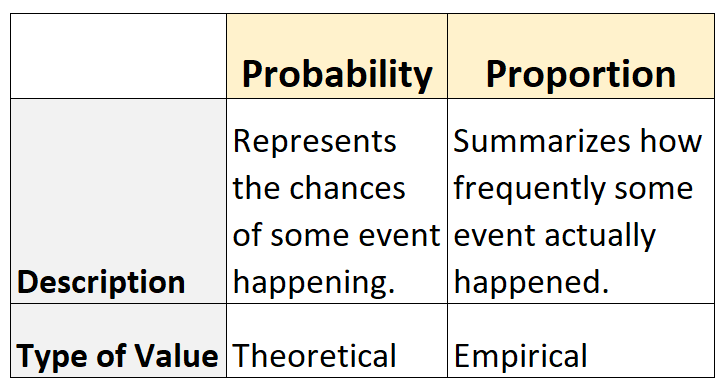
Twee termen die studenten vaak verwarren in de statistiek zijn waarschijnlijkheid en proportie .

Hier is het verschil:

• Waarschijnlijkheid vertegenwoordigt de kans dat een gebeurtenis plaatsvindt. Het is theoretisch .
• De verhouding geeft een samenvatting van hoe vaak een gebeurtenis daadwerkelijk heeft plaatsgevonden. Het is empirisch .

We gebruiken waarschijnlijkheid vaak om te praten over de kansen dat een gebeurtenis in de toekomst zal plaatsvinden.

Daarentegen gebruiken we vaak proporties om te beschrijven hoe vaak een gebeurtenis in het verleden daadwerkelijk heeft plaatsgevonden.

De volgende voorbeelden illustreren de verschillen tussen kansen en verhoudingen in verschillende scenario’s.

Voorbeeld 1: Waarschijnlijkheid versus proportie bij het opgooien van munten

Als we een eerlijke munt opgooien, is de kans dat deze kop oplevert 0,5 of 50% .

Als we echter twintig keer een munt opgooien, kunnen we feitelijk tellen hoeveel keer er kop is gevallen. Hij kan bijvoorbeeld 60% van de tijd dat hij gooit met kop komen.

De waarschijnlijkheid dat de munt kop oplevert is theoretisch, maar het percentage keren dat de munt kop oplevert is empirisch – we zouden deze verhouding zelfs kunnen tellen.

Voorbeeld 2: Waarschijnlijkheid versus verhouding bij dobbelstenenworpen

Als u een zeszijdige dobbelsteen gooit, is de kans dat deze op het cijfer “4” valt 1/6 of ongeveer 16,67% .

Als we de dobbelsteen echter 10 keer gooien, kunnen we het aantal keren tellen dat hij op 4 terecht is gekomen. Misschien is hij bijvoorbeeld in 20% van de worpen op „4“ terechtgekomen.

De waarschijnlijkheid dat je een “4” gooit is theoretisch, maar het aantal keren dat de dobbelsteen op een “4” terechtkomt is empirisch – we zouden dit percentage ook daadwerkelijk kunnen tellen.

Voorbeeld 3: Waarschijnlijkheid vs. Verhouding in spinners

Als we een roulettewiel laten draaien dat in vier gelijke delen is verdeeld – rood, blauw, groen en paars – is de kans dat het bij een bepaalde draai op paars belandt 25% .

Als we het roulettewiel echter 100 keer laten draaien, kunnen we het aantal keren tellen dat het op paars is beland. Misschien belandde hij bijvoorbeeld voor 15% van de spins op paars.

De waarschijnlijkheid dat het roulettewiel op paars belandt is theoretisch, maar het aantal keren dat het roulettewiel op paars belandt is empirisch – we zouden het percentage zelfs kunnen tellen.

Voorbeeld 4: Waarschijnlijkheid versus evenredigheid in kaartspellen

In een standaard kaartspel van 52 kaarten zijn er 4 Koninginnen. De kans dat je bij een trekking een dame kiest, is dus 4/52 = 7,69% .

Als we echter 50 keer willekeurig trekken (en de kaart die we trekken vervangen), kunnen we feitelijk het aantal keren tellen dat we een koningin trekken. Misschien trekken we bijvoorbeeld in 10% van de trekkingen een dame.

De waarschijnlijkheid dat we een koningin kiezen is theoretisch, maar het aantal keren dat we daadwerkelijk een koningin kiezen is empirisch – we zouden het percentage daadwerkelijk kunnen tellen.

Aanvullende bronnen

Waarschijnlijkheid versus waarschijnlijkheid: wat is het verschil?
Wet van de totale waarschijnlijkheid: definitie en voorbeelden