Wanneer moet je correlatie gebruiken? (uitleg & voorbeelden)

Correlatie wordt gebruikt om de lineaire associatie tussen twee variabelen te meten.

Een correlatiecoëfficiënt heeft altijd een waarde tussen -1 en 1 waarbij:

• -1 geeft een perfect negatieve lineaire correlatie aan tussen twee variabelen
• 0 geeft aan dat er geen lineaire correlatie is tussen twee variabelen
• 1 geeft een perfect positieve lineaire correlatie aan tussen twee variabelen

Een vraag die studenten vaak stellen is: wanneer moet ik correlatie gebruiken?

Het korte antwoord: gebruik correlatie als u de lineaire relatie tussen twee variabelen wilt kwantificeren en geen van beide variabelen een respons- of „uitkomstvariabele“ vertegenwoordigt .

De volgende voorbeelden illustreren wanneer u in de praktijk wel en niet correlatie moet gebruiken.

Voorbeeld 1: Wanneer correlatie gebruiken

Stel dat een professor inzicht wil krijgen in de lineaire relatie tussen de scores van wiskundetoetsen en de scores van de natuurkundetoetsen van de leerlingen in zijn klas.

Doen leerlingen die goed presteren op het wiskunde-examen het bijvoorbeeld ook goed op het natuurkunde-examen? Of scoren leerlingen die hoog scoren op wiskunde vaak laag op natuurwetenschappen?

In dit scenario zou hij de correlatie tussen de scores van wiskunde-examens en de scores van natuurkunde-examens kunnen berekenen, omdat hij alleen de lineaire relatie tussen de twee variabelen wil begrijpen en geen van beide variabelen als een responsvariabele kan worden beschouwd.

Stel dat hij dePearson-correlatiecoëfficiënt berekent en ontdekt dat deze r = 0,78 is. Dit is een sterke positieve correlatie, wat betekent dat leerlingen die goed presteren in wiskunde ook vaak goed presteren in natuurwetenschappen.

Voorbeeld 2: Wanneer u geen correlatie gebruikt

Stel dat de marketingafdeling van een bedrijf de impact van advertentie-uitgaven op de totale omzet wil kwantificeren.

Hoeveel extra inkomsten kan het bedrijf bijvoorbeeld verwachten te verdienen voor elke extra dollar die aan advertenties wordt uitgegeven?

In dit scenario moet de afdeling een lineair regressiemodel gebruiken om de relatie tussen advertentie-uitgaven en totale inkomsten te kwantificeren, omdat de variabele ‚opbrengst‘ de responsvariabele is.

Stel dat de afdeling een eenvoudig lineair regressiemodel toepast en tot de conclusie komt dat de volgende vergelijking de relatie tussen advertentie-uitgaven en totale inkomsten het beste beschrijft:

Totale opbrengst = 145,4 + 0,34*(advertentiekosten)

We interpreteren dit zo dat elke extra dollar die aan advertenties wordt besteed, resulteert in een gemiddelde stijging van de totale inkomsten met $ 0,34.

Voorzorgsmaatregelen voor het gebruik van correlatie

Het is belangrijk op te merken dat correlatie alleen kan worden gebruikt om de lineaire relatie tussen twee variabelen te kwantificeren.

Onder bepaalde omstandigheden zal een correlatiecoëfficiënt echter niet in staat zijn om effectief een verband vast te leggen tussen twee variabelen die een niet-lineair verband delen.

Stel dat we bijvoorbeeld het volgende spreidingsdiagram maken om de relatie tussen twee variabelen te visualiseren:

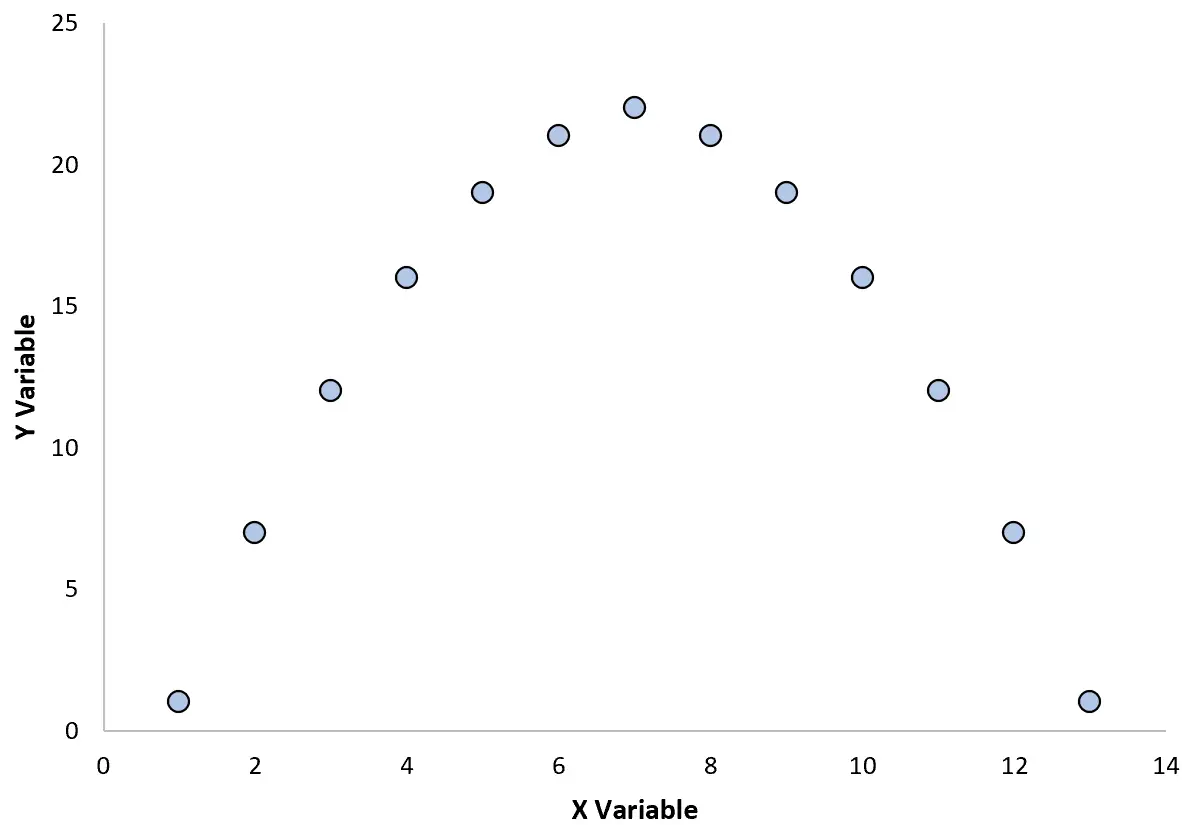
Als we de correlatiecoëfficiënt tussen deze twee variabelen berekenen, blijkt deze r = 0 te zijn. Dit betekent dat er geen lineair verband bestaat tussen de twee variabelen.

Uit de grafiek kunnen we echter zien dat de twee variabelen inderdaad een relatie hebben: het is eenvoudigweg een kwadratische relatie in plaats van een lineaire relatie.

Houd er dus bij het berekenen van de correlatie tussen twee variabelen rekening mee dat het ook nuttig kan zijn om een spreidingsdiagram te maken om de relatie tussen de variabelen te visualiseren.

Zelfs als twee variabelen geen lineair verband hebben, is het mogelijk dat ze een niet-lineair verband hebben, wat zichtbaar zou worden in een spreidingsdiagram.

Aanvullende bronnen

In de volgende tutorials wordt gedetailleerder uitgelegd hoe correlatie in verschillende omstandigheden wordt gebruikt:

6 praktijkvoorbeelden van correlatie
Wat wordt beschouwd als een “sterke” correlatie?
Correlatie versus vereniging: wat is het verschil?
Correlatie versus regressie: wat is het verschil?