Wanneer moet u polynomiale regressie gebruiken?

Polynomiale regressie is een techniek die we kunnen gebruiken om een regressiemodel te fitten wanneer de relatie tussen de voorspellende variabele(n) en de responsvariabele niet-lineair is.

Een polynoomregressiemodel heeft de volgende vorm:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

In de praktijk zijn er drie eenvoudige manieren om te bepalen of u polynomiale regressie moet gebruiken in plaats van een eenvoudiger model zoals lineaire regressie .

1. Maak een spreidingsdiagram van de voorspellende variabele en de responsvariabele

De eenvoudigste manier om te bepalen of u polynomiale regressie moet gebruiken, is door een eenvoudig spreidingsdiagram te maken van de voorspellende variabele en de responsvariabele.

Laten we bijvoorbeeld zeggen dat we de voorspellende variabele ’studie-uren‘ willen gebruiken om te voorspellen welk cijfer een leerling zal krijgen op een eindexamen.

Voordat we een regressiemodel passen, kunnen we eerst een spreidingsdiagram maken van de bestudeerde uren ten opzichte van de examenresultaten. Stel dat ons spreidingsdiagram er als volgt uitziet:

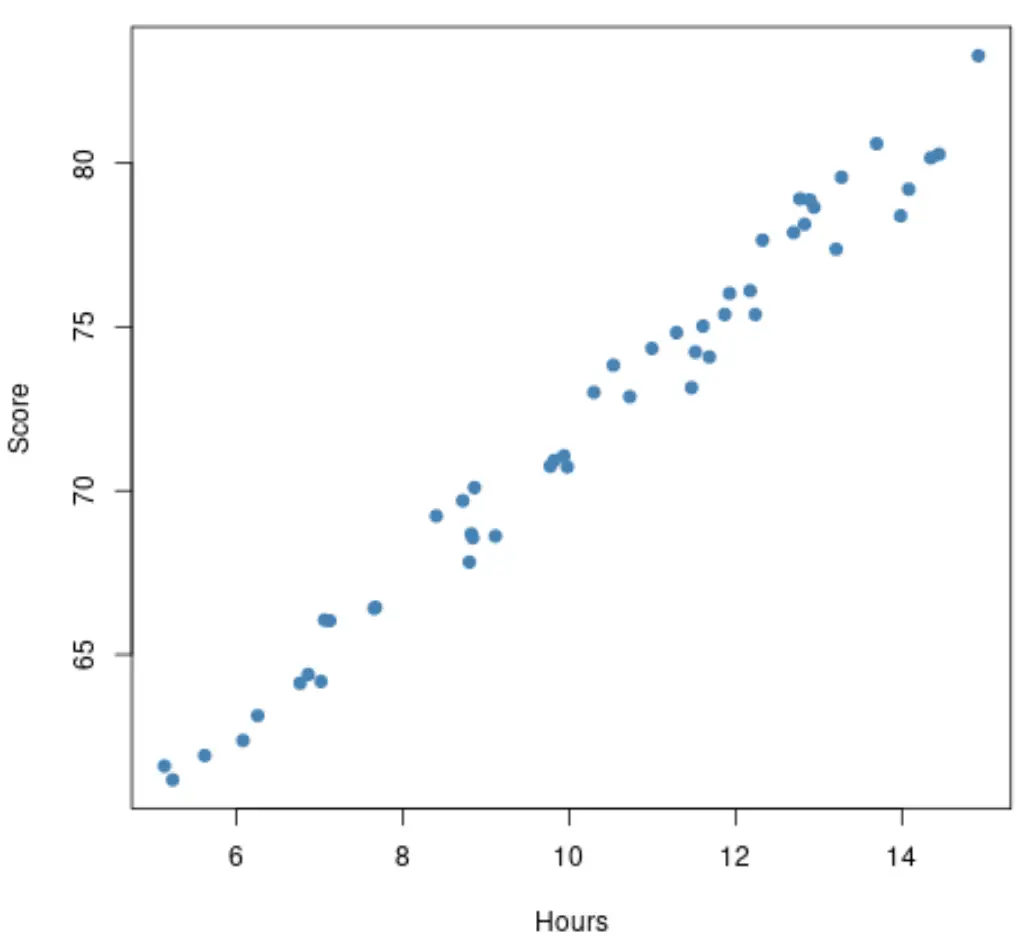
De relatie tussen het aantal gestudeerde uren en de examenresultaten lijkt lineair , dus het zou zinvol zijn om een eenvoudig lineair regressiemodel aan deze dataset toe te passen.

Laten we echter aannemen dat het spreidingsdiagram er feitelijk als volgt uitziet:

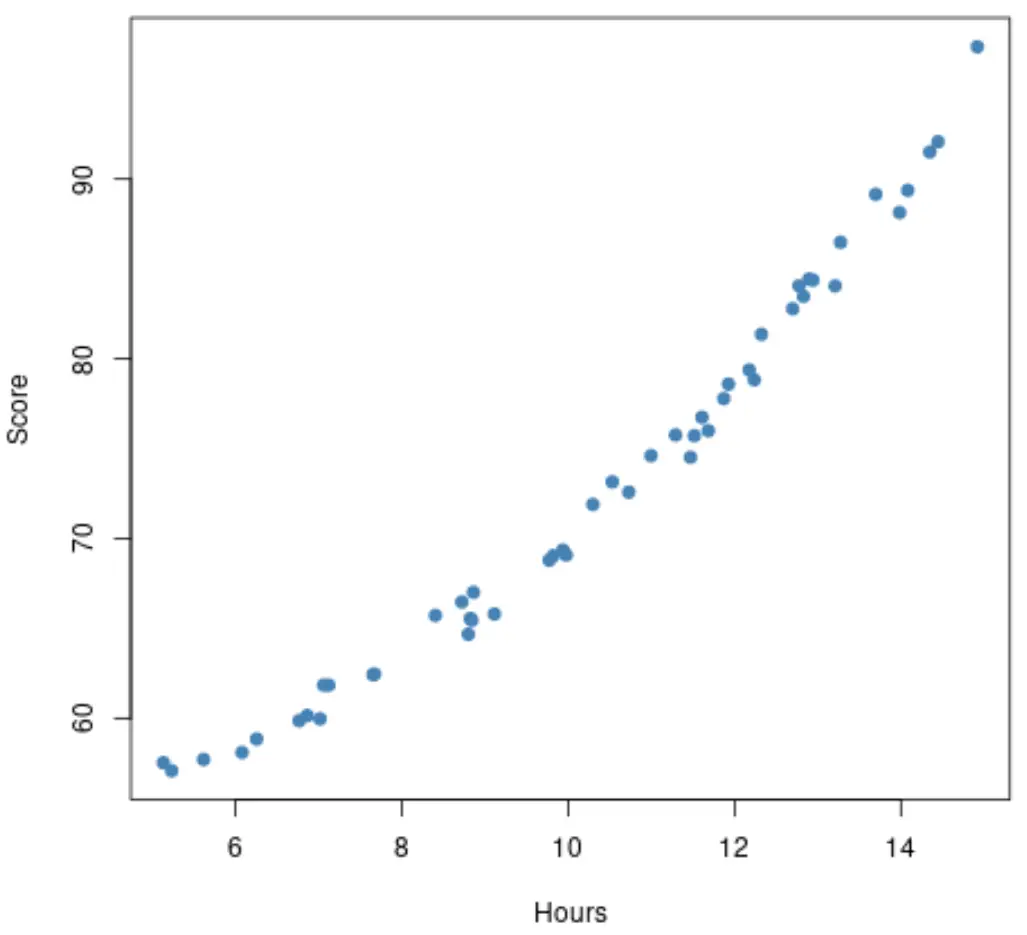
Deze relatie lijkt iets meer niet-lineair , wat ons vertelt dat het verstandig kan zijn om in plaats daarvan een polynomiaal regressiemodel te gebruiken.

2. Maak een grafiek van de gepaste en restwaarden

Een andere manier om te bepalen of u polynomiale regressie moet gebruiken, is door een lineair regressiemodel aan de dataset te koppelen en vervolgens een grafiek van de aangepaste waarden te maken tegen de residuen voor het model.

Als er een duidelijke niet-lineaire trend in de residuen aanwezig is, geeft dit aan dat polynomiale regressie mogelijk een betere aansluiting op de gegevens oplevert.

Stel dat we bijvoorbeeld een lineair regressiemodel passen met bestudeerde uren als voorspellende variabele en examenscore als responsvariabele, en vervolgens de volgende grafiek van aangepaste waarden maken tegen de residuen:

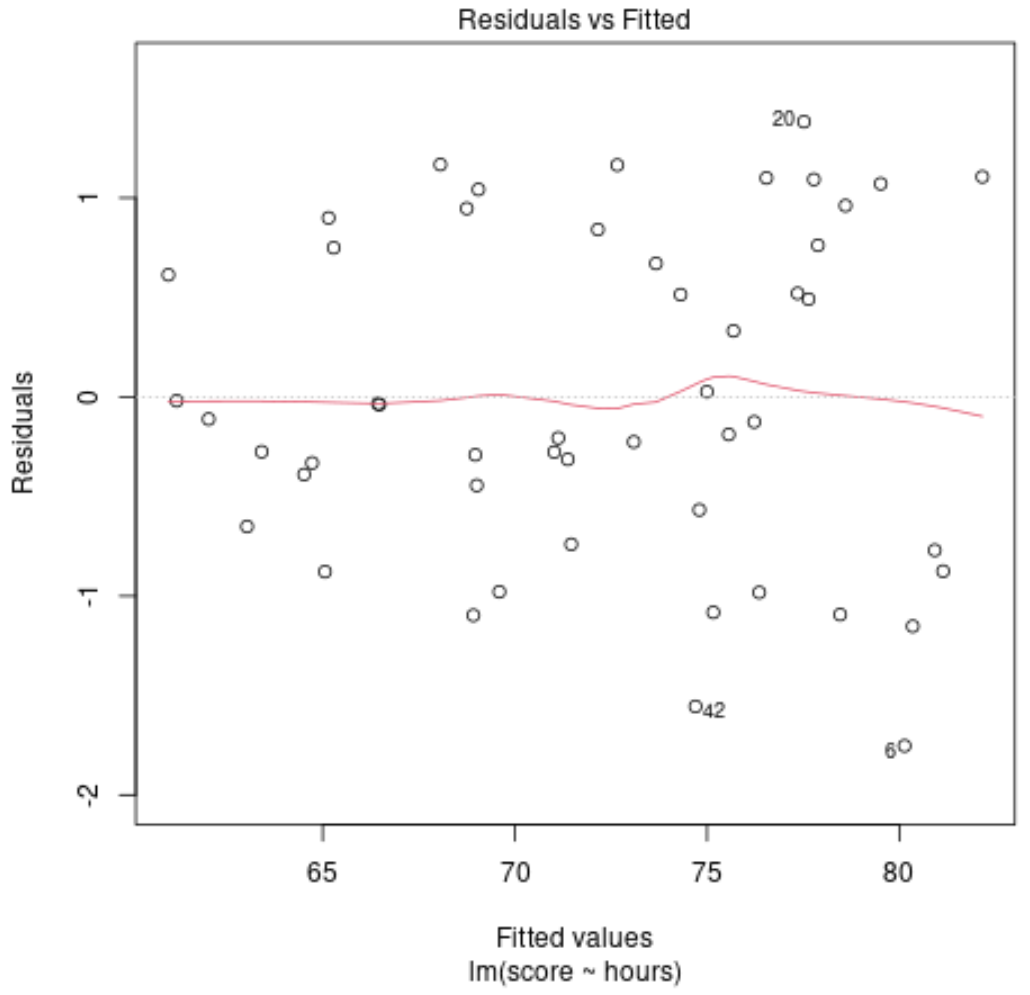
De residuen zijn willekeurig rond nul verspreid, zonder duidelijk patroon, wat aangeeft dat een lineair model een goede aansluiting op de gegevens biedt.

Laten we echter aannemen dat onze grafiek van aangepaste waarden versus residuen er feitelijk als volgt uitziet:

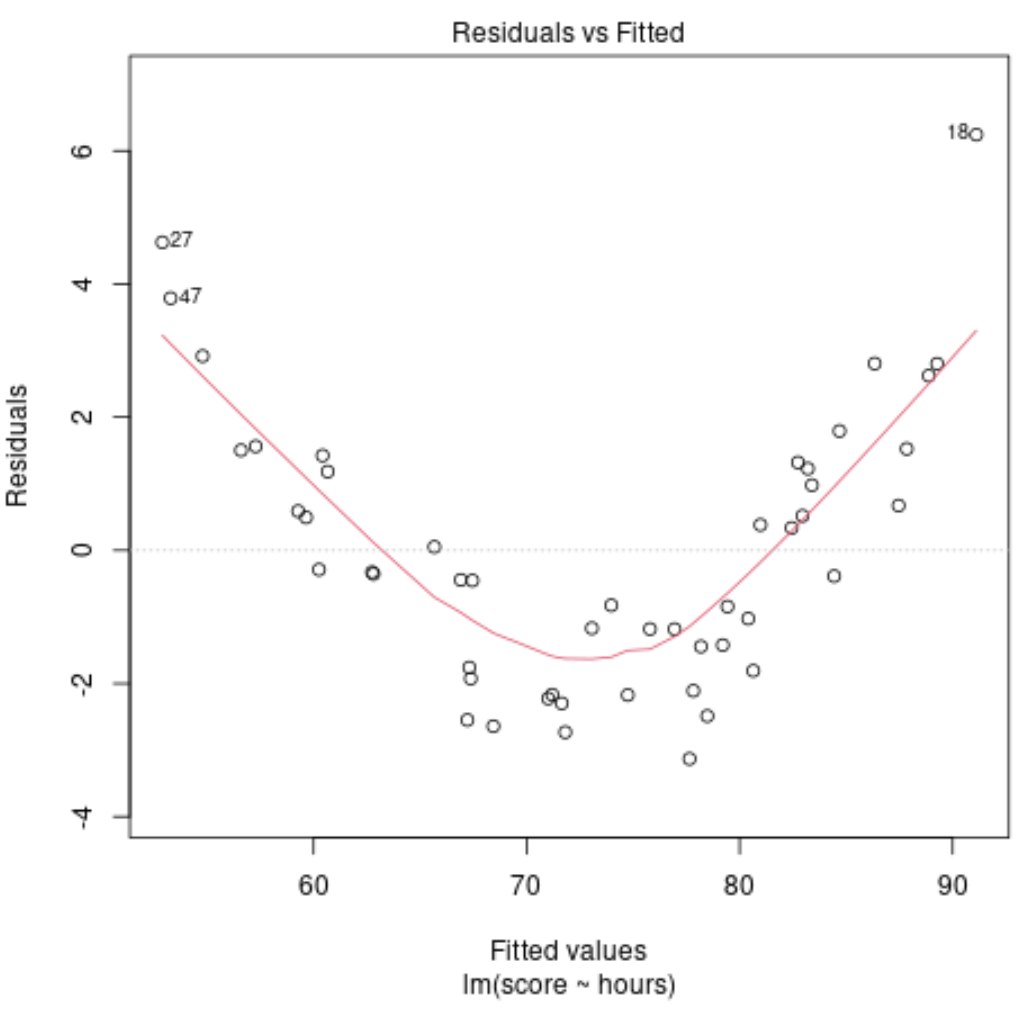
Uit de grafiek kunnen we zien dat er een duidelijk niet-lineair patroon in de residuen zit: de residuen vertonen een “U”-vorm.

Dit vertelt ons dat een lineair model niet geschikt is voor deze specifieke gegevens en dat het verstandig zou kunnen zijn om in plaats daarvan een polynoom regressiemodel te gebruiken.

3. Bereken de aangepaste R-kwadraatwaarde van het model

Een andere manier om te bepalen of u polynomiale regressie moet gebruiken, is door zowel een lineair regressiemodel als een polynomiaal regressiemodel te fitten en de aangepaste R-kwadraatwaarden voor beide modellen te berekenen.

De aangepaste R-kwadraat vertegenwoordigt het deel van de variantie in de responsvariabele dat kan worden verklaard door de voorspellende variabelen in het model, aangepast voor het aantal voorspellende variabelen in het model.

Het model met het hoogste aangepaste R-vierkant vertegenwoordigt het model dat het beste in staat is de voorspellende variabele(n) te gebruiken om de variatie in de responsvariabele te verklaren.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u polynomiale regressie kunt uitvoeren met behulp van verschillende statistische software:

Een inleiding tot polynomiale regressie
Hoe polynomiale regressie uit te voeren in R
Hoe polynomiale regressie uit te voeren in Python
Hoe polynomiale regressie uit te voeren in Excel