Wanneer moet u de spearman-rangcorrelatie gebruiken (2 scenario's)

De meest gebruikelijke manier om de lineaire associatie tussen twee variabelen te kwantificeren is door dePearson-correlatiecoëfficiënt te gebruiken, die altijd een waarde tussen -1 en 1 aanneemt, waarbij:

• -1 duidt op een volkomen negatieve lineaire correlatie
• 0 geeft aan dat er geen lineaire correlatie is
• 1 geeft een perfect positieve lineaire correlatie aan

Dit type correlatiecoëfficiënt werkt echter het beste wanneer de werkelijke onderliggende relatie tussen de twee variabelen lineair is.

Er is een ander type correlatiecoëfficiënt, de Spearman-rangcorrelatie , die het best in twee specifieke scenario’s kan worden gebruikt:

Scenario 1 : Bij het werken met geheime gegevens.

• Een voorbeeld zou een dataset kunnen zijn die de rangschikking van de wiskunde-examenscore van een leerling bevat, evenals de rangschikking van zijn wetenschapsexamenscore in een klas.

Scenario 2 : Wanneer er één of meer extreme uitschieters aanwezig zijn.

• Wanneer extreme uitschieters aanwezig zijn in een dataset, wordt de Pearson-correlatiecoëfficiënt sterk beïnvloed.

De volgende voorbeelden laten zien hoe u de Spearman-rangcorrelatie in elk van deze scenario’s kunt berekenen.

Scenario 1: Spearman-ranking correleren met gerangschikte gegevens

Beschouw de volgende gegevensset (en de bijbehorende spreidingsdiagram) die de relatie tussen twee variabelen laat zien:

Met behulp van statistische software kunnen we voor deze twee variabelen de volgende correlatiecoëfficiënten berekenen:

• Pearson-correlatie: 0,79
• Spearman-rangcorrelatie: 1

Als we in dit scenario alleen maar om de rangorde van de gegevenswaarden geven (als de rangorde van x toeneemt, neemt dan ook de rangorde van y toe?), dan zou de rangcorrelatie van Spearman ons een beter idee geven van de correlatie tussen de twee variabelen. .

In deze specifieke dataset geldt dat naarmate de rangorde van x toeneemt, de rangorde van y altijd toeneemt.

De rangcorrelatie van Spearman geeft dit gedrag perfect weer door ons te vertellen dat er een perfecte positieve relatie ( ρ = 1 ) bestaat tussen de rangen van x en de rangen van y.

Aan de andere kant vertelt de Pearson-correlatie ons dat er een sterke lineaire relatie ( r = 0,79 ) bestaat tussen de twee variabelen.

Dit is waar, maar het is niet nuttig als we ons alleen maar bekommeren om de relatie tussen de rangen van x en de rangen van y.

Scenario 2: Correlatie van de Spearman-ranglijst met extreme uitschieters

Beschouw de volgende gegevensset (en de bijbehorende spreidingsdiagram) die de relatie tussen twee variabelen laat zien:

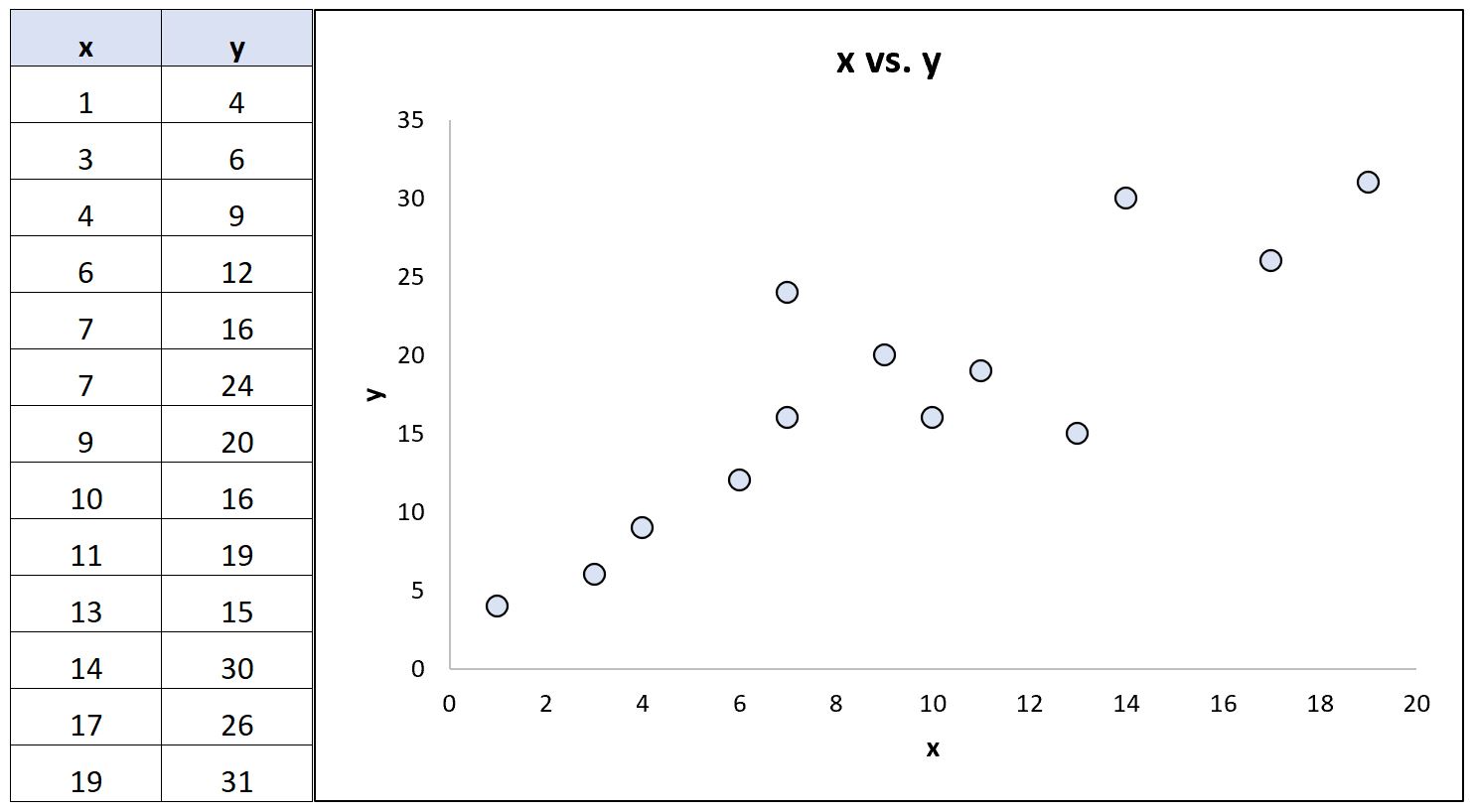
Met behulp van statistische software kunnen we voor deze twee variabelen de volgende correlatiecoëfficiënten berekenen:

• Pearson-correlatie: 0,86
• Spearman-rangcorrelatie: 0,85

De correlatiecoëfficiënten zijn vrijwel identiek omdat de onderliggende relatie tussen de variabelen bij benadering lineair is en er geen extreme uitschieters zijn.

Stel nu dat we de laatste y-waarde in de dataset veranderen, zodat deze een extreme uitbijter wordt:

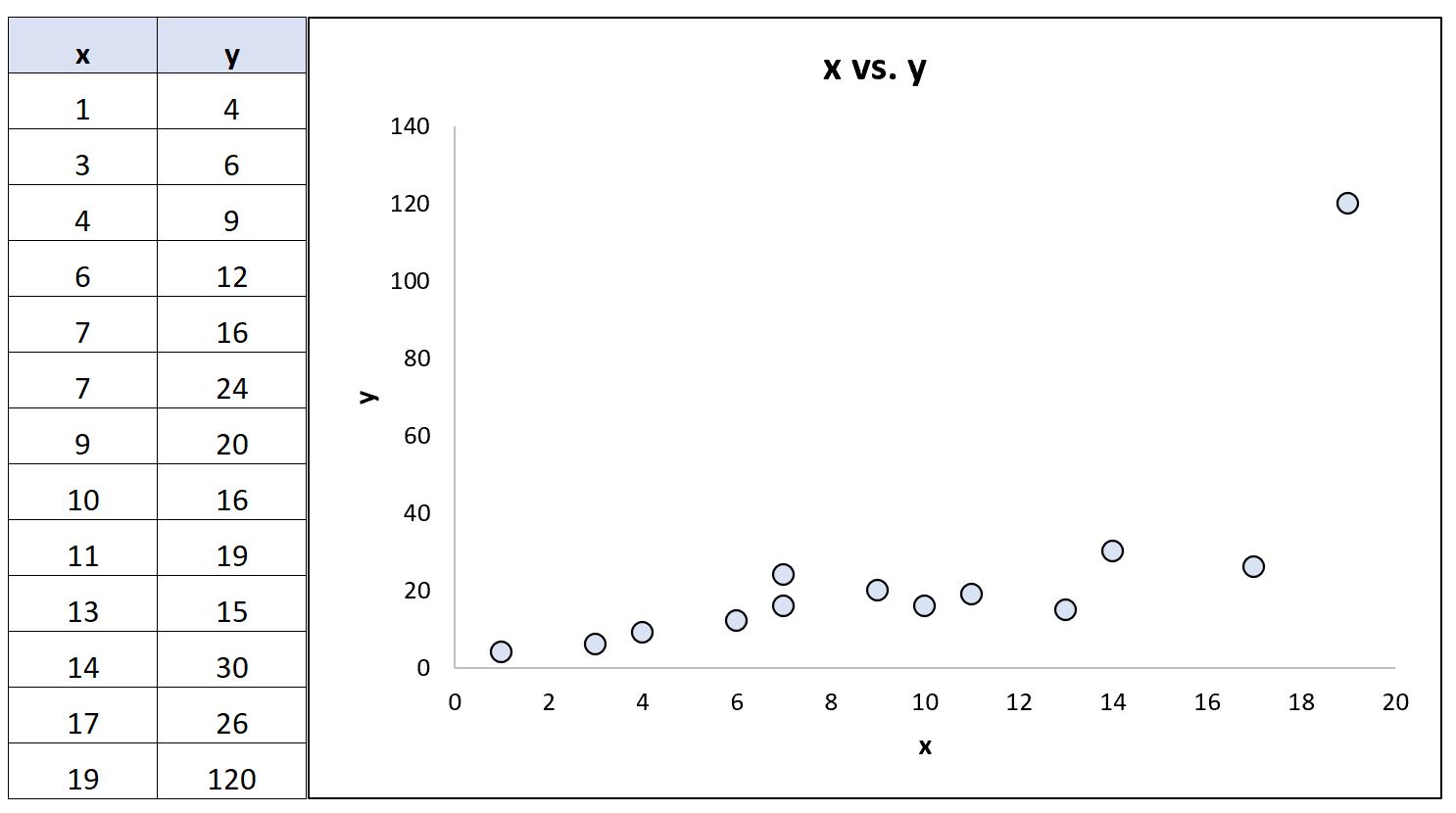
Met behulp van statistische software kunnen we de correlatiecoëfficiënten herberekenen:

• Pearson-correlatie: 0,69
• Spearman-rangcorrelatie: 0,85

De Pearson-correlatiecoëfficiënt veranderde aanzienlijk, terwijl de Spearman-rangcorrelatiecoëfficiënt hetzelfde bleef.

In statistisch jargon zouden we zeggen dat de relatie tussen x en y monotoon is (als x toeneemt, neemt y doorgaans toe), maar niet lineair, aangezien de uitbijter de gegevens sterk beïnvloedt.

In dit scenario kwantificeert de rangcorrelatie van Spearman deze monotone relatie goed, terwijl de correlatie van Pearson het slecht doet omdat deze probeert de lineaire relatie tussen de twee variabelen te berekenen.

Gerelateerd: Spearman-rangcorrelatie rapporteren in APA-indeling

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u de Spearman-rangcorrelatie kunt berekenen met behulp van verschillende software:

Hoe Spearman Rank-correlatie in Excel te berekenen
Hoe u de Spearman-rangcorrelatie in Google Spreadsheets kunt berekenen
Hoe de Spearman-rangcorrelatie in R te berekenen
Hoe de Spearman Rank-correlatie in Python te berekenen