Wanneer moet je een boxplot gebruiken? (3 scenario's)

Een boxplot is een type plot dat de vijfcijferige samenvatting van een dataset weergeeft, waaronder:

• De minimumwaarde
• Het eerste kwartiel (het 25e percentiel)
• De gemiddelde waarde
• Het derde kwartiel (het 75e percentiel)
• De maximale waarde

We gebruiken drie eenvoudige stappen om een boxplot voor elke dataset te maken:

• 1. Teken een kader van het eerste tot en met het derde kwartiel
• 2. Teken een verticale lijn op de mediaan
• 3. Teken de “snorharen” van de kwartielen naar de minimum- en maximumwaarde

Normaal gesproken maken we boxplots in een van de volgende drie scenario’s:

Scenario 1: Visualiseer de verdeling van waarden in een dataset.

Met een boxplot kunnen we snel de verdeling van waarden in een dataset visualiseren en zien waar de vijf numerieke samenvattende waarden zich bevinden.

Scenario 2: Om twee of meer distributies te vergelijken.

Side-by-side boxplots stellen ons in staat de verschillen tussen twee of meer verdelingen te visualiseren en de mediaanwaarden en verdeling van waarden tussen verdelingen te vergelijken.

Scenario 3: Uitschieters identificeren.

In boxplots worden uitschieters meestal weergegeven door kleine cirkels die voorbij elke snorhaar reiken. Een waarneming wordt als uitbijter gedefinieerd als deze aan een van de volgende criteria voldoet:

• Een waarneming is minder dan Q1 – 1,5*(interkwartielafstand)
• Een waarneming is groter dan Q3 + 1,5*(interkwartielafstand)

Door een boxplot te maken, kunnen we snel zien of een verdeling wel of geen uitschieters heeft.

De volgende voorbeelden laten zien hoe we in elk scenario een boxplot zouden gebruiken.

Scenario 1: Visualiseer de verdeling van waarden in een dataset

Stel dat een basketbalcoach de verdeling van de door de spelers van zijn team gescoorde punten wil visualiseren en daarom de volgende boxplot maakt:

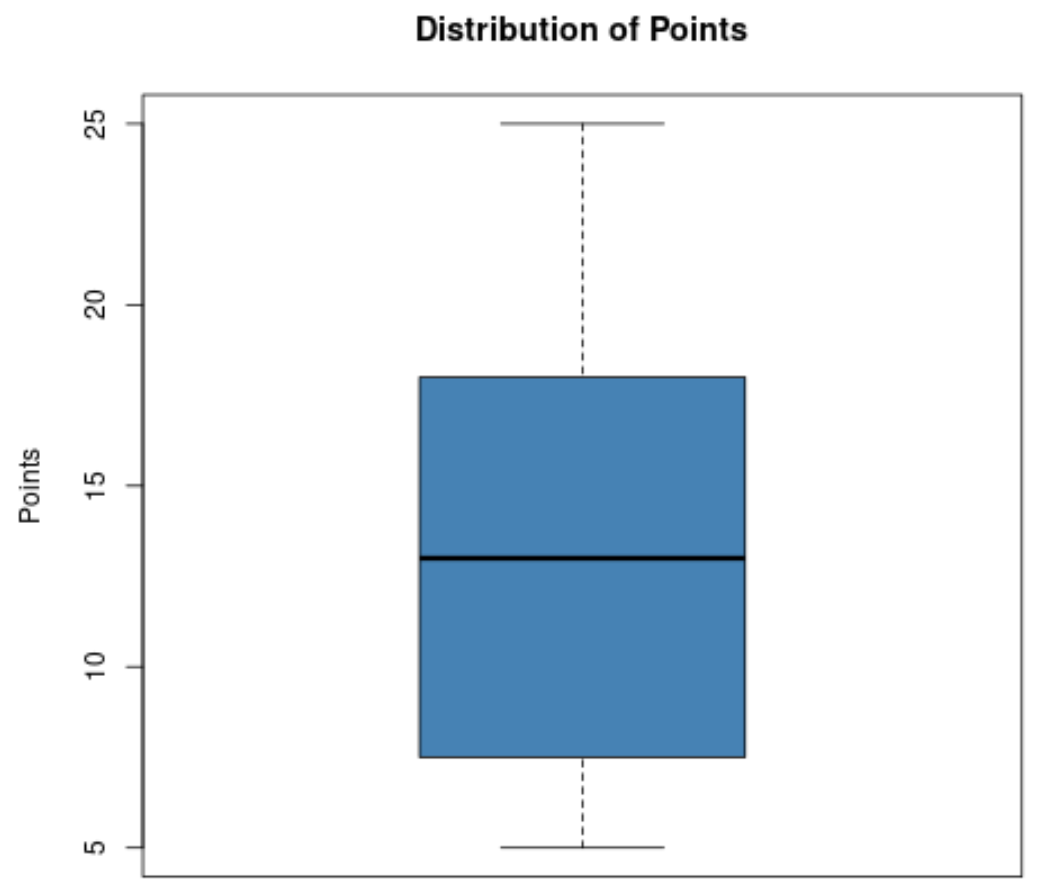
Op basis van deze boxplot kan hij snel de volgende waarden zien:

• Minimaal: 5
• T1 (eerste kwartiel): ongeveer 8
• Mediaan: rond de 13
• T3 (derde kwartiel): ongeveer 18
• Maximaal: 25

Hierdoor kan de coach snel zien dat de door spelers gescoorde punten variëren van 5 tot 25, dat de gemiddelde gescoorde punten ongeveer 13 zijn en dat 50% van zijn spelers tussen ongeveer 8 en 18 punten per wedstrijd scoort.

Scenario 2: Vergelijk twee of meer distributies

Stel dat een sportanalist de verdeling van de punten wil vergelijken die zijn gescoord door basketbalspelers in drie verschillende teams en de volgende boxplots wil maken:

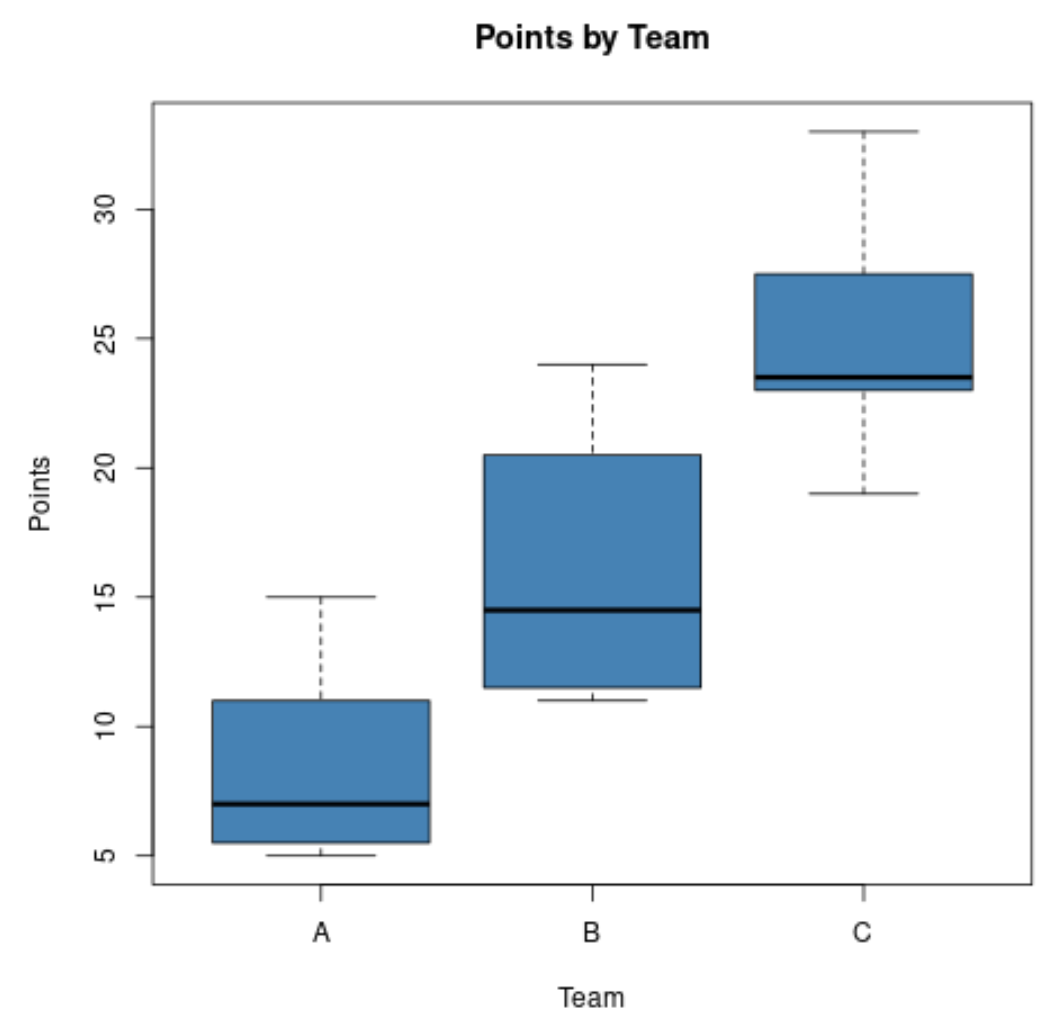
Met behulp van deze grafieken kan hij snel zien dat team C de hoogste middelpunten heeft gescoord en dat team A de laagste middelpunten heeft gescoord.

Hij kan ook snel zien dat team B de grootste verdeling van gescoorde punten heeft, aangezien de boxplot van team B de langste box heeft.

Scenario 3: Identificeer uitschieters

Stel dat een basketbalcoach wil weten of een van zijn spelers een uitschieter is qua gescoorde punten. Hij besluit de volgende boxplot te maken om de verdeling van de door zijn spelers gescoorde punten te visualiseren:

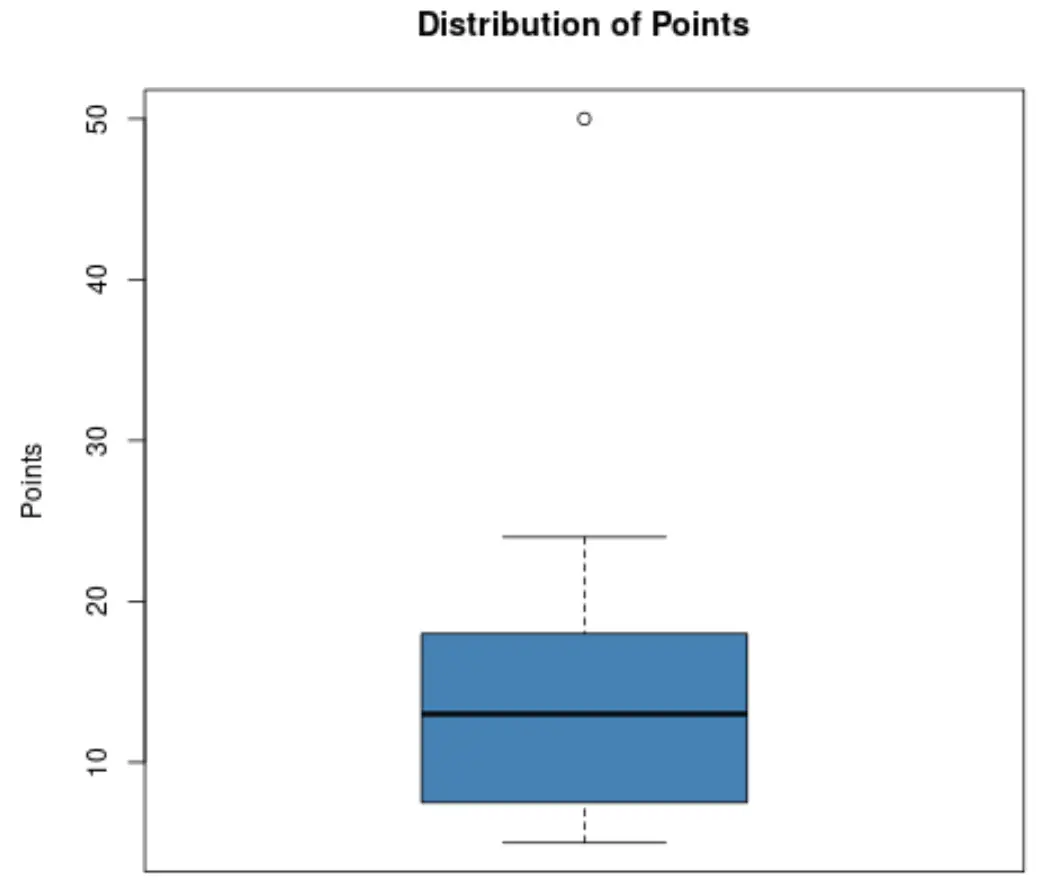
Met behulp van deze grafiek kan de coach zien dat de kleine stip bovenaan de grafiek een uitschieter aangeeft.

Concreet scoorde een van de spelers ongeveer 50 punten, wat als een uitschieter wordt beschouwd in vergelijking met alle andere gescoorde punten.

Aanvullende bronnen

De volgende tutorials bieden gedetailleerde uitleg over het gebruik van boxplots in de praktijk:

Hoe u de interkwartielafstand (IQR) van een boxplot kunt vinden
Hoe asymmetrie in boxplots te identificeren
Boxplots vergelijken

In de volgende tutorials wordt uitgelegd hoe u boxplots maakt in verschillende statistische software:

Hoe u een boxplot maakt in Google Spreadsheets
Boxplots maken in SPSS
Hoe u zij-aan-zij boxplots kunt maken in Excel
Hoe u side-by-side boxplots maakt in R