Wat betekent een hoge f-waarde in anova?
Een eenrichtings-ANOVA wordt gebruikt om te bepalen of de gemiddelden van drie of meer onafhankelijke groepen al dan niet gelijk zijn.
Een eenrichtings-ANOVA gebruikt de volgende nul- en alternatieve hypothesen:
- H 0 : Alle groepsgemiddelden zijn gelijk.
- H A : Minstens één groepsgemiddelde verschilt van de andere.
Elke keer dat u een eenrichtings-ANOVA uitvoert, krijgt u een samenvattende tabel die er als volgt uitziet:
| Bron | Som van kwadraten (SS) | df | Gemiddelde kwadraten (MS) | F | P-waarde |
|---|---|---|---|---|---|
| Behandeling | 192,2 | 2 | 96,1 | 2.358 | 0,1138 |
| Fout | 1100,6 | 27 | 40,8 | ||
| Totaal | 1292,8 | 29 |
De F-waarde in de tabel wordt als volgt berekend:
- F-waarde = gemiddelde kwadratenverwerking / gemiddelde kwadratenfout
Een andere manier om dit te schrijven is:
- F-waarde = variatie tussen steekproefgemiddelden / variatie binnen steekproeven
Als de variatie tussen de steekproefgemiddelden hoog is vergeleken met de variatie binnen elk van de monsters, zal de F-waarde groot zijn.
De F-waarde in de bovenstaande tabel wordt bijvoorbeeld als volgt berekend:
- F-waarde = 96,1 / 40,8 = 2,358
Om de p-waarde te vinden die overeenkomt met deze F-waarde, kunnen we een F-verdelingscalculator gebruiken met vrijheidsgraden in de teller = df Behandeling en vrijheidsgraden in de noemer = df Fout.
De p-waarde die overeenkomt met een F-waarde van 2,358, de teller df = 2 en de noemer df = 27 is bijvoorbeeld 0,1138 .
Omdat deze p-waarde niet kleiner is dan α = 0,05, slagen we er niet in de nulhypothese te verwerpen. Dit betekent dat er geen statistisch significant verschil bestaat tussen de gemiddelden van de drie groepen.
Bekijk de F-waarde van een ANOVA
Om een intuïtief inzicht te krijgen in de F-waarde in een ANOVA-tabel, kunt u het volgende voorbeeld overwegen.
Stel dat we een one-way ANOVA willen uitvoeren om te bepalen of drie verschillende studietechnieken verschillende gemiddelde examenscores opleveren. De volgende tabel toont de examenresultaten van 10 studenten die elke techniek gebruikten:
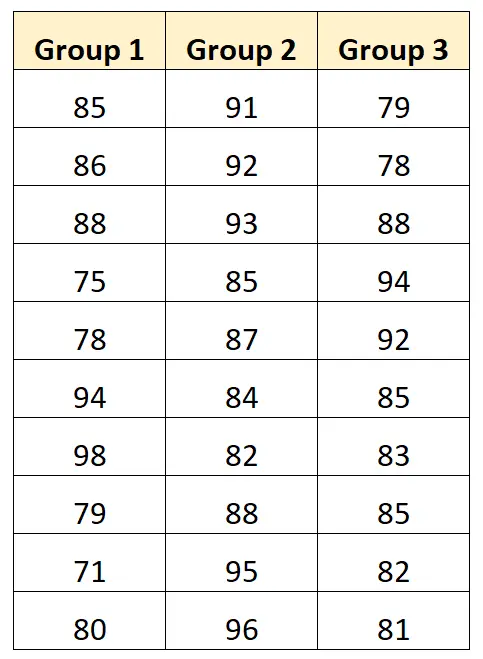
We kunnen het volgende diagram maken om de examenresultaten per groep te visualiseren:
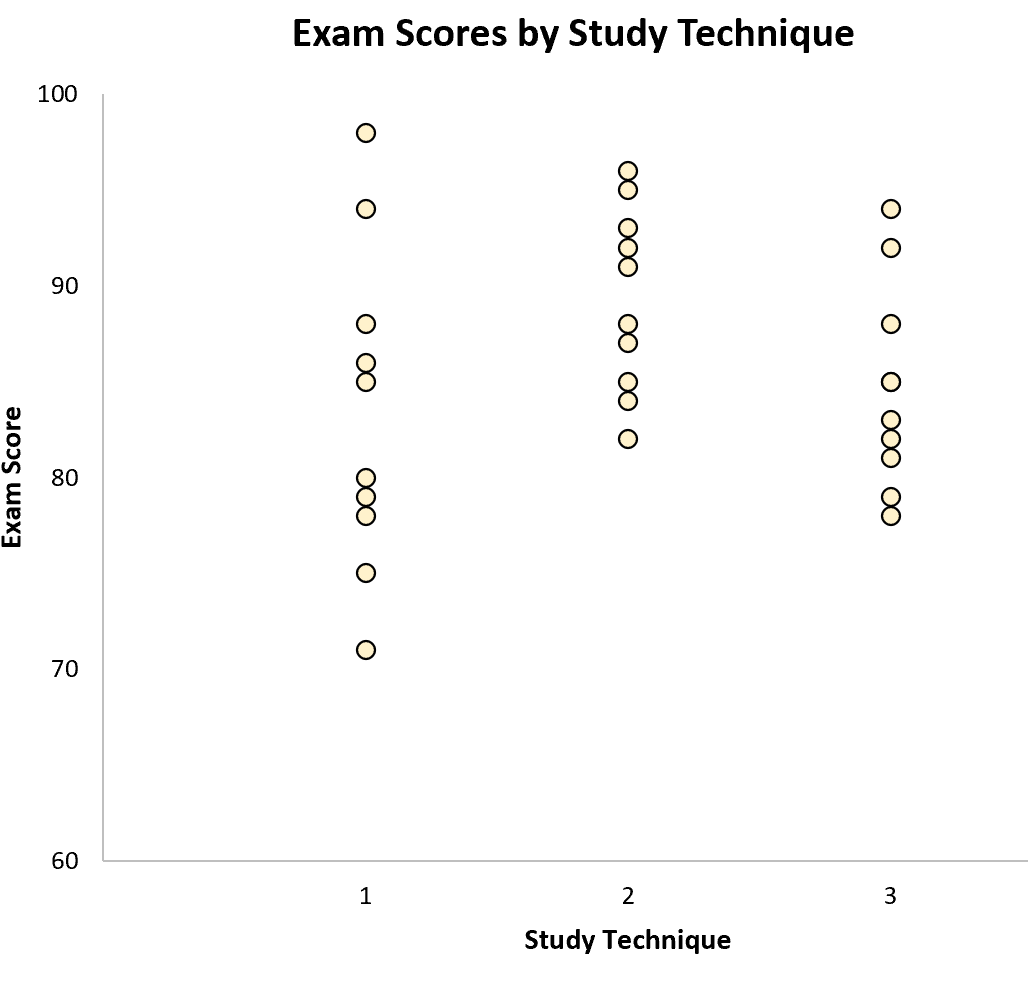
De variatie binnen monsters wordt weergegeven door de verdeling van waarden binnen elk afzonderlijk monster:
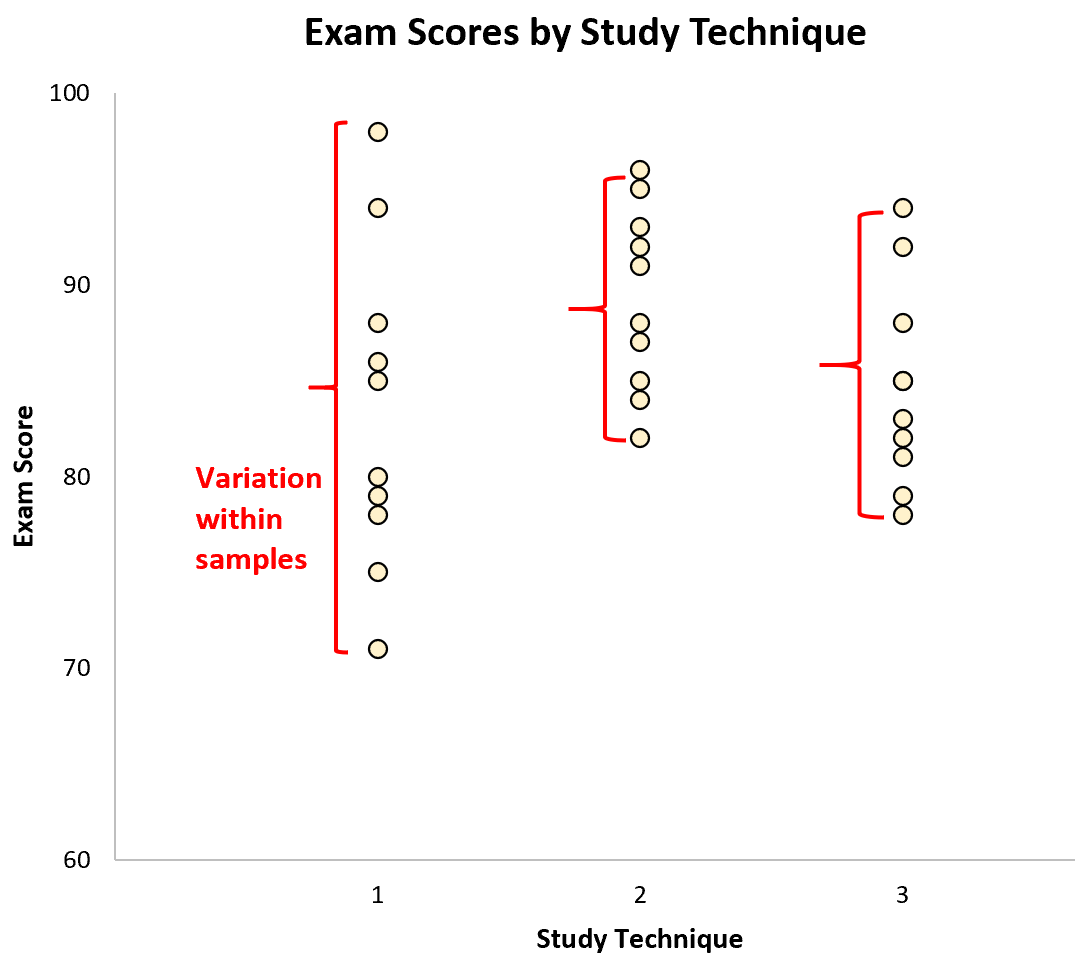
De variatie tussen monsters wordt weergegeven door de verschillen tussen de steekproefgemiddelden:
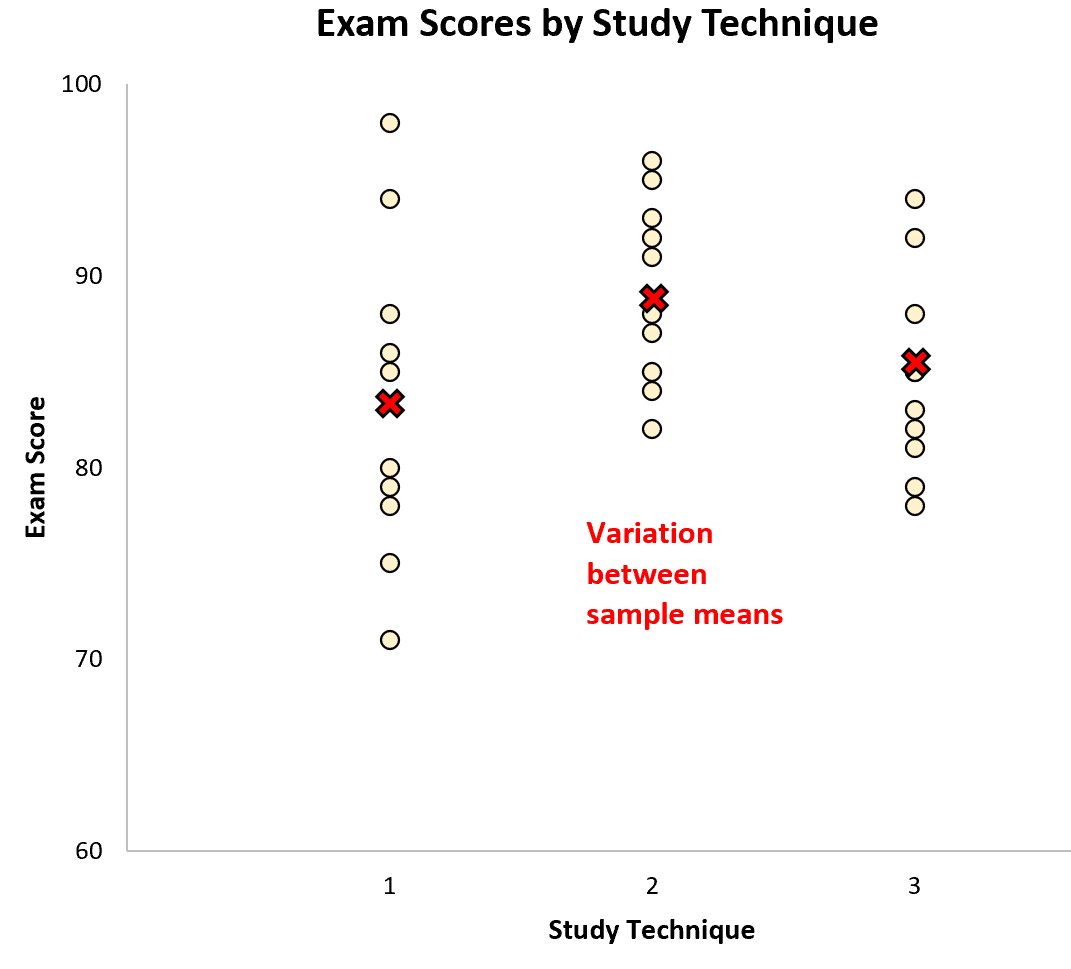
Als we een eenrichtings-ANOVA uitvoeren voor deze dataset, ontdekken we dat de F-waarde 2,358 is en de overeenkomstige p-waarde 0,1138 .
Omdat deze p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen. Dit betekent dat we onvoldoende bewijs hebben om te zeggen dat de gebruikte onderzoekstechniek resulteert in statistisch significante verschillen in gemiddelde examenscores.
Met andere woorden, dit vertelt ons dat de variatie tussen de steekproefgemiddelden niet hoog genoeg is in verhouding tot de variatie binnen de steekproeven om de nulhypothese te verwerpen.
Conclusie
Hier volgt een korte samenvatting van de belangrijkste punten van dit artikel:
- De F-waarde in een ANOVA wordt berekend als: variatie tussen steekproefgemiddelden / variatie binnen steekproeven.
- Hoe hoger de F-waarde in een ANOVA, hoe groter de variatie tussen steekproefgemiddelden ten opzichte van de variatie binnen steekproeven.
- Hoe hoger de F-waarde, hoe lager de overeenkomstige p-waarde.
- Als de p-waarde onder een bepaalde drempel ligt (bijvoorbeeld α = 0,05), kunnen we de nulhypothese van de ANOVA verwerpen en concluderen dat er een statistisch significant verschil bestaat tussen de groepsgemiddelden.
Aanvullende bronnen
Eenrichtings-ANOVA uitvoeren in Excel
Hoe u handmatig een eenrichtings-ANOVA uitvoert
One-way ANOVA-calculator