Wat betekent het als een statistiek veerkrachtig is?

Een statistiek heet veerkrachtig als deze niet gevoelig is voor extreme waarden.

Hier zijn twee voorbeelden van veerkrachtige statistieken:

• De mediaan
• De interkwartielafstand

Hier zijn voorbeelden van statistieken die geen stand houden :

• Het gemiddelde
• De standaardafwijking
• Netjes

Het volgende voorbeeld illustreert het verschil tussen veerkrachtige en niet-resistente statistieken.

Voorbeeld: resistente en niet-resistente statistieken

Stel dat we de volgende dataset hebben:

Gegevensset: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29

Met behulp van een rekenmachine of statistische software kunnen we de waarde van de volgende holdingstatistieken voor deze dataset berekenen:

• Mediaan: 13
• Interkwartielafstand: 13,5

We kunnen ook de waarde berekenen van de volgende niet-veerkrachtige statistieken voor deze dataset:

• Gemiddeld: 13,54
• Standaardafwijking: 8,82
• Bereik: 27

Overweeg nu of aan deze dataset een extreme uitbijter is toegevoegd:

Gegevensset: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29, 450

We kunnen opnieuw de waarde berekenen van de volgende veerkrachtige statistieken voor deze dataset:

• Mediaan: 14
• Interkwartielafstand: 15,75

We kunnen ook de waarde berekenen van de volgende niet-veerkrachtige statistieken voor deze dataset:

• Gemiddeld: 49,92
• Standaardafwijking: 126,27
• Bereik: 448

Merk op hoeveel de niet-resistentiestatistieken veranderden door simpelweg een extreme waarde aan de dataset toe te voegen:

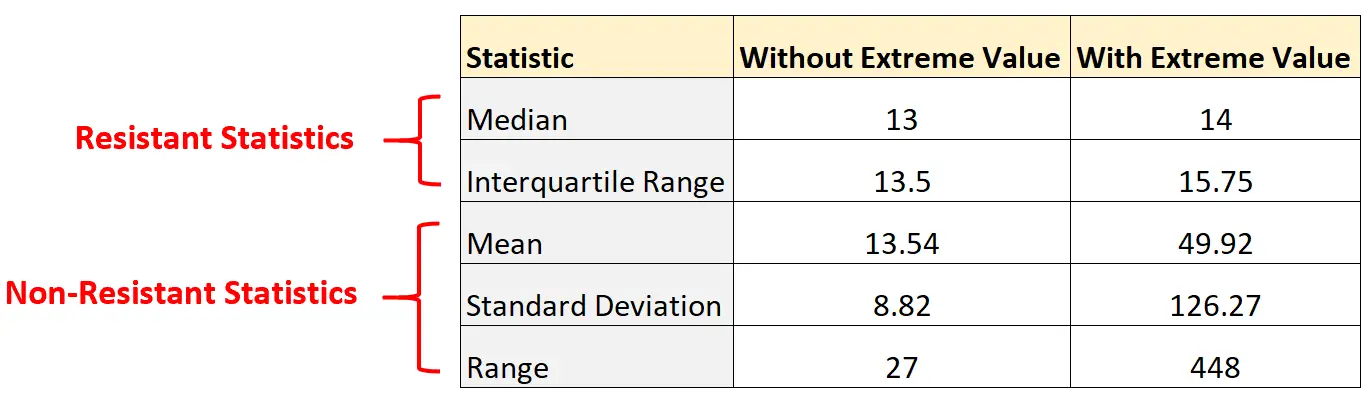
Omgekeerd zijn de statistieken van de verzetsstrijders nauwelijks veranderd. De mediaan en de interkwartielafstand veranderden slechts in geringe mate.

Wanneer veerkrachtige statistieken gebruiken?

De meest gebruikte statistieken om het centrum en de spreiding van waarden in een dataset te meten zijn respectievelijk het gemiddelde en de standaarddeviatie.

Helaas zijn beide statistieken gevoelig voor extreme waarden. Als er dus uitschieters in een dataset aanwezig zijn, zullen het gemiddelde en de standaarddeviatie de verdeling van de waarden in een dataset niet nauwkeurig beschrijven.

In plaats daarvan wordt aanbevolen om het mediaan- en interkwartielbereik te gebruiken om het centrum en de spreiding van waarden in een dataset te meten als er uitschieters aanwezig zijn, aangezien beide statistieken robuust zijn.

Aanvullende bronnen

Hoe beïnvloeden uitbijters het gemiddelde?
Wanneer moet u het gemiddelde versus de mediaan gebruiken?
Wanneer interkwartielbereik versus standaarddeviatie gebruiken?