Weibull-distributie

Von Dr.benjamin anderson August 3, 2023 Waarschijnlijkheid Keine Kommentare

In dit artikel wordt uitgelegd wat de Weibull-distributie is en waarvoor deze wordt gebruikt. Bovendien kunt u de grafische weergave van de Weibull-verdeling zien en wat de eigenschappen zijn van dit type kansverdeling.

Wat is de Weibull-verdeling?

De Weibull-verdeling is een continue kansverdeling die wordt gedefinieerd door twee karakteristieke parameters: de vormparameter α en de schaalparameter λ.

In de statistieken wordt de Weibull-verdeling voornamelijk gebruikt voor overlevingsanalyse. Op dezelfde manier heeft de Weibull-distributie veel toepassingen op verschillende gebieden. Hieronder gaan we dieper in op het gebruik van de Weibull-distributie.

$X\sim\text{Weibull}(\alpha,\lambda)$

Volgens de auteurs kan de Weibull-verdeling ook worden geparametriseerd met drie parameters. Vervolgens wordt een derde parameter, drempelwaarde genaamd, toegevoegd, die de abscis aangeeft waarop de verdelingsgrafiek begint.

De Weibull-verdeling is vernoemd naar de Zweed Waloddi Weibull, die deze in 1951 gedetailleerd beschreef. De Weibull-verdeling werd echter in 1927 ontdekt door Maurice Fréchet en voor het eerst toegepast door Rosin en Rammler in 1933.

De Weibull-verdeling in kaart brengen

Zodra we de definitie van de Weibull-verdeling hebben gezien, zullen we zien hoe de grafische weergave ervan varieert afhankelijk van de waarden van de parameters.

Hieronder ziet u verschillende voorbeelden van hoe de dichtheidsfunctiegrafiek van de Weibull-verdeling varieert, afhankelijk van de waarde van de vormparameter en de schaalparameter.

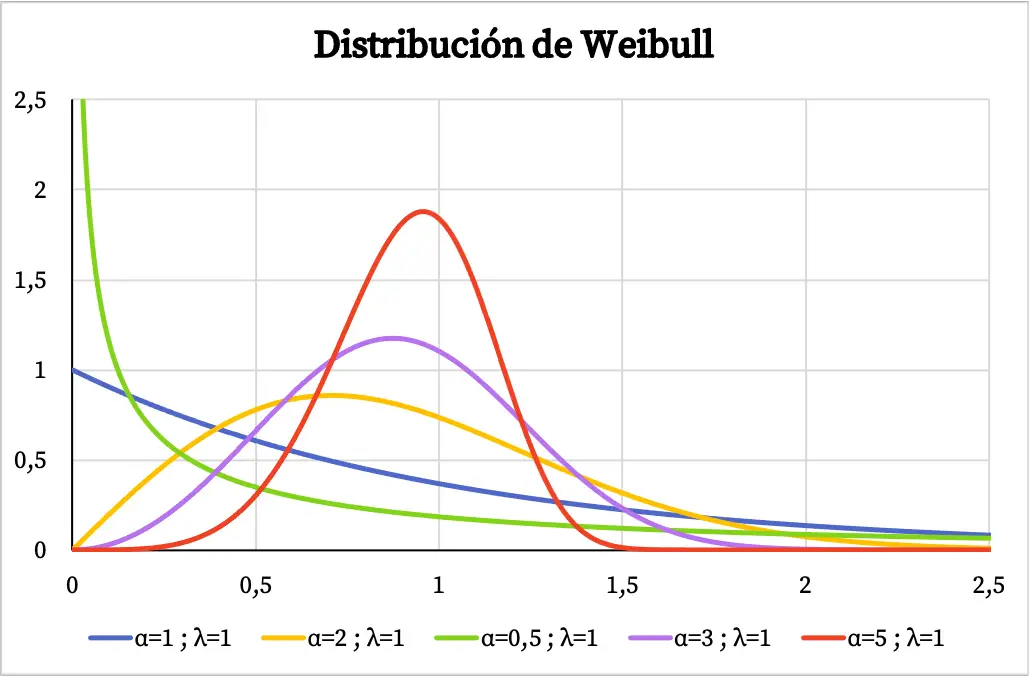
Wanneer de Weibull-verdeling wordt gebruikt om het uitvalpercentage van een systeem als functie van de tijd te modelleren, betekent de waarde van de vormparameter α het volgende:

α<1: het uitvalpercentage neemt in de loop van de tijd af.
α=1: het faalpercentage is constant in de tijd.
α>1: het percentage mislukkingen neemt in de loop van de tijd toe.

Aan de andere kant kunt u in de volgende grafiek de cumulatieve waarschijnlijkheidsfunctie van de Weibull-verdeling zien, uitgezet op basis van de karakteristieke waarden.

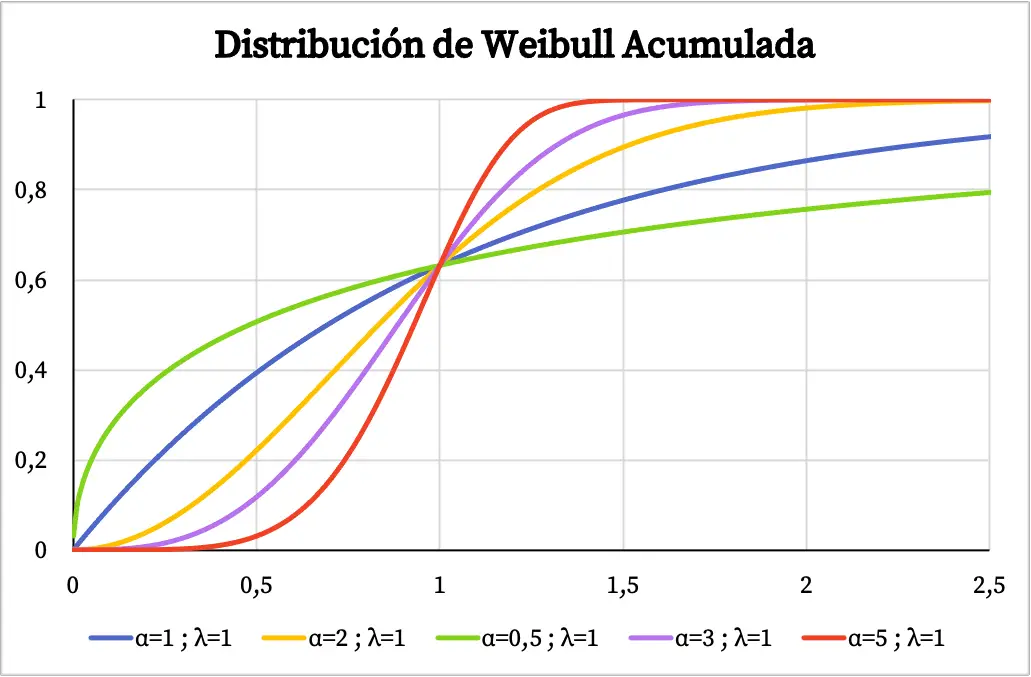
cumulatieve waarschijnlijkheid van de Weibull-verdeling

Kenmerken van de Weibull-verdeling

De Weibull-verdeling heeft de volgende kenmerken:

De Weibull-verdeling heeft twee karakteristieke parameters die de grafiek definiëren: de vormparameter α en de schaalparameter λ. Beide parameters zijn positieve reële getallen.

$\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}“ title=“Rendered by QuickLaTeX.com“ height=“92″ width=“101″ style=“vertical-align: 0px;“></p> </p> <ul> <li> De Weibull-verdeling accepteert alleen positieve absciswaarden.</li> </ul> <p class=$ $x\in (0,+\infty)$

Het gemiddelde van de Weibull-verdeling wordt berekend met de volgende formule:

$\displaystyle E[X]=\frac{1}{\lambda}\;\Gamma\left(1+\frac{1}{\alpha}\right)$

Aan de andere kant is de formule voor het vinden van de variantie van de Weibull-verdeling:

$\displaystyle Var(X)=\frac{1}{\lambda^2}\left[\Gamma\left(1+\frac{2}{\alpha}\right)-\Gamma^2\left(1+\frac{1}{\alpha}\right)\right]$

De modus van een willekeurige variabele die een Weibull-verdeling volgt met α>1 kan worden bepaald door de volgende uitdrukking:

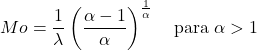
$\displaystyle Mo=\frac{1}{\lambda}\left(\frac{\alpha-1}{\alpha} \right)^{\frac{1}{\alpha}} \quad \text{para } \alpha>1″ title=“Rendered by QuickLaTeX.com“ height=“50″ width=“257″ style=“vertical-align: -17px;“></p> </p> <ul> <li> De formule voor de dichtheidsfunctie van de Weibull-verdeling is:</li> </ul> <p class=$ $\displaystyle P[X=x]=\lambda\alpha(\lambda x)^{\alpha-1}e^{-(\lambda x)^\alpha}$

Op dezelfde manier is de formule voor de cumulatieve waarschijnlijkheidsfunctie van de Weibull-verdeling:

$\displaystyle P[X\leq x]=1- e^{-(\lambda x)^\alpha}$

De asymmetriecoëfficiënt van de Weibull-verdeling wordt berekend door de volgende formule toe te passen:

$\displaystyle A=\frac{\displaystyle\Gamma\left(1+\frac{3}{\alpha}\right)\frac{|}{\lambda^3}-3\mu\sigma^2-\mu^3}{\sigma^3}$

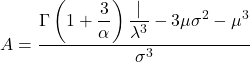
Ten slotte is de formule die het mogelijk maakt om de kurtosis-coëfficiënt van de Weibull-verdeling te bepalen de volgende:

$\displaystyle C=\frac{\displaystyle\frac{1}{\lambda^4}\Gamma \left(1+\frac{4}{\alpha}\right)-4\gamma_{1}\sigma^3\mu-6\mu^2\sigma^2-\mu^4}{\sigma^4}$

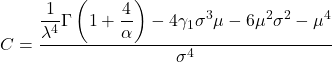
Goud

$\Gamma_i=\Gamma\left(1+\frac{i}{\alpha}\right).$

Toepassingen van de Weibull-distributie

De Weibull-distributie kent vele toepassingen, waaronder:

In de toegepaste statistiek wordt de Weibull-verdeling gebruikt bij overlevingsanalyses.
In de techniek wordt de Weibull-verdeling gebruikt om functies te modelleren die verband houden met de productietijd.
In radarsystemen, om de verspreiding van het ontvangen signaal te simuleren.
In de verzekeringssector, om de omvang van claims te modelleren.
In de meteorologie bijvoorbeeld om de frequentie van verschillende windsnelheden te modelleren.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder