Hoe de t-test van welch uit te voeren in r

De t-test van Welch wordt gebruikt om gemiddelden tussen twee onafhankelijke groepen te vergelijken, wanneer niet wordt aangenomen dat de twee groepen gelijke varianties hebben.

Om de t-test van Welch in R uit te voeren, kunnen we de functie t.test() gebruiken, die de volgende syntaxis gebruikt:

t.test(x, y, alternatief = c(“twee gezichten”, “minder”, “groter”))

Goud:

• x: een numerieke vector van gegevenswaarden voor de eerste groep
• y: een numerieke vector van gegevenswaarden voor de tweede groep
• alternatief: de alternatieve hypothese voor de test. De standaardinstelling is dubbelzijdig.

In het volgende voorbeeld ziet u hoe u deze functie kunt gebruiken om de Welch’s t-test in R uit te voeren.

Voorbeeld: Welch’s t-test in R

Een docent wil de examenresultaten vergelijken van twaalf leerlingen die een toetsvoorbereidingsboekje hebben gebruikt ter voorbereiding op een examen, en die van twaalf leerlingen die dat niet hebben gedaan.

De volgende vectoren tonen de examenresultaten van studenten in elke groep:

 booklet <- c(90, 85, 88, 89, 94, 91, 79, 83, 87, 88, 91, 90)
no_booklet <- c(67, 90, 71, 95, 88, 83, 72, 66, 75, 86, 93, 84)

Voordat we een Welch’s t-test uitvoeren, kunnen we eerst boxplots maken om de verdeling van de scores voor elke groep te visualiseren:

 boxplot(booklet, no_booklet, names =c(" Booklet "," No Booklet "))

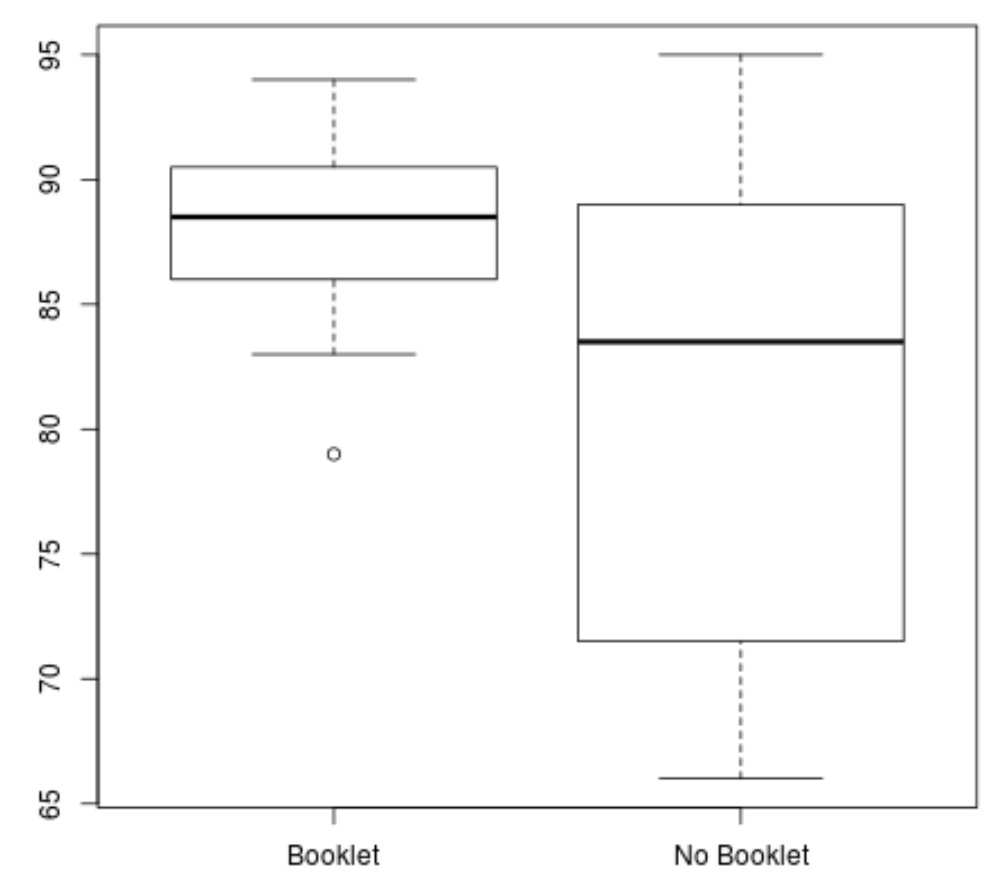
We kunnen duidelijk zien dat de groep “Boekje” een hogere gemiddelde score en een lagere scorevariantie heeft.

Om formeel te testen of de gemiddelde scores tussen groepen significant verschillen, kunnen we de t-test van Welch uitvoeren:

 #perform Welch's t-test
t.test(booklet, no_booklet)

	Welch Two Sample t-test

data: booklet and no_booklet
t = 2.2361, df = 14.354, p-value = 0.04171
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
  0.3048395 13.8618272
sample estimates:
mean of x mean of y 
 87.91667 80.83333 

Uit het resultaat kunnen we zien dat de t -teststatistiek 2,2361 is en de overeenkomstige p-waarde 0,04171 .

Omdat deze p-waarde kleiner is dan 0,05 kunnen we de nulhypothese verwerpen en concluderen dat er een statistisch significant verschil bestaat in de gemiddelde examenscores tussen de twee groepen.

De functie t.test() biedt ons ook de volgende informatie:

• Het 95% betrouwbaarheidsinterval voor het verschil in gemiddelde examenscores tussen de twee groepen is [0,3048, 13,8618 ].
• De gemiddelde examenscore van de eerste groep bedraagt 87,91667 .
• De gemiddelde examenscore van de tweede groep bedraagt 80,83333 .

De volledige documentatie voor de functie t.test() vindt u hier .

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in R kunt uitvoeren:

Hoe voer je een one-sample t-test uit in R
Hoe voer je een t-test met twee steekproeven uit in R
Hoe voer je een paired samples t-test uit in R
Hoe meerdere boxplots in één grafiek in R te plotten