Hoe de t-test van welch in excel uit te voeren

De meest gebruikelijke manier om gemiddelden tussen twee onafhankelijke groepen te vergelijken, is door een t-test met twee steekproeven te gebruiken. Deze test gaat er echter van uit dat de varianties tussen de twee groepen gelijk zijn.

Als u denkt dat de variantie tussen de twee groepen niet gelijk is , kunt u de t-test van Welch gebruiken, wat het niet-parametrische equivalent is van de t-test met twee steekproeven.

In deze tutorial wordt uitgelegd hoe u de Welch’s t-test in Excel uitvoert.

Voorbeeld: Welch’s t-test in Excel

Voor dit voorbeeld vergelijken we de resultaten van 12 studenten die een examenvoorbereidingsboekje gebruikten om zich voor te bereiden op het examen, versus 12 studenten die dat niet deden.

Gebruik de volgende stappen om een Welch’t-test uit te voeren om te bepalen of er een verschil is in de gemiddelde examenscores tussen de twee groepen.

Stap 1: Voer de gegevens in.

Voer eerst de examenresultaten in twee kolommen in:

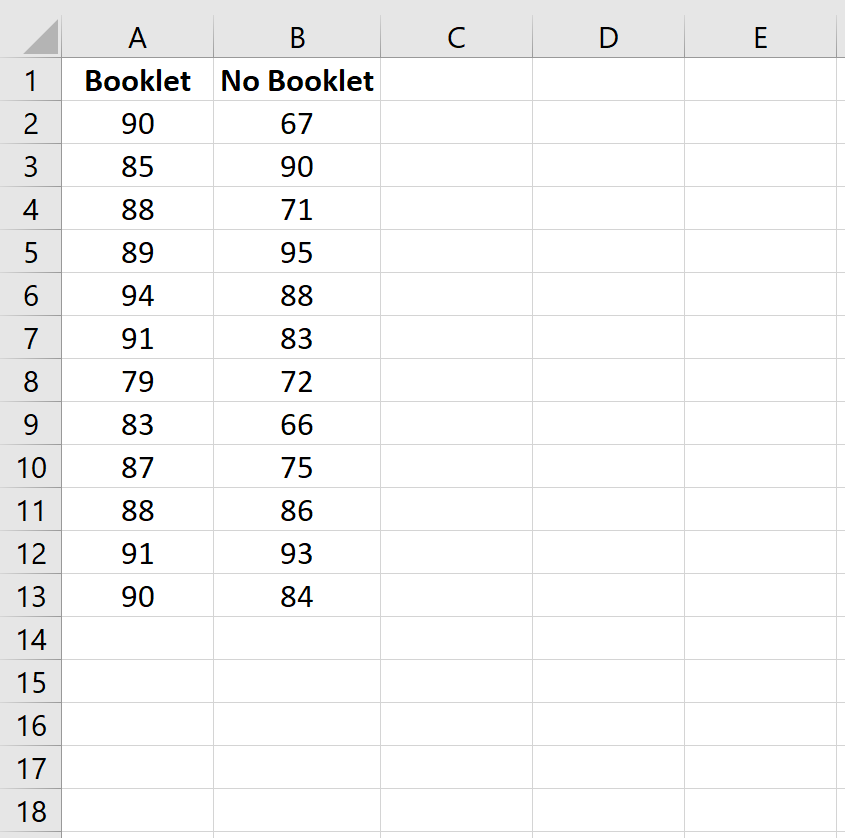
Stap 2: Voer de t-test van Welch uit.

Ga op het bovenste lint van Excel naar het tabblad Gegevens en klik op Gegevensanalyse . Als u deze optie niet ziet, moet u eerst de gratis Analysis ToolPak-software installeren .

Zodra u op Data-analyse klikt, verschijnt een nieuw venster. Selecteer t-test: twee steekproeven gaan uit van ongelijke varianties en klik op OK .

Voer in het nieuwe venster het bereik van gegevenswaarden in voor Variabele 1 en Variabele 2 , inclusief hun groepslabels. Voor Hypothetisch gemiddeld verschil typt u 0. Vink het vakje naast Labels aan. Laat Alfa ingesteld op 0,05. Kies bij Uitvoerbereik een cel waar u de testresultaten wilt laten verschijnen. Klik vervolgens op OK .

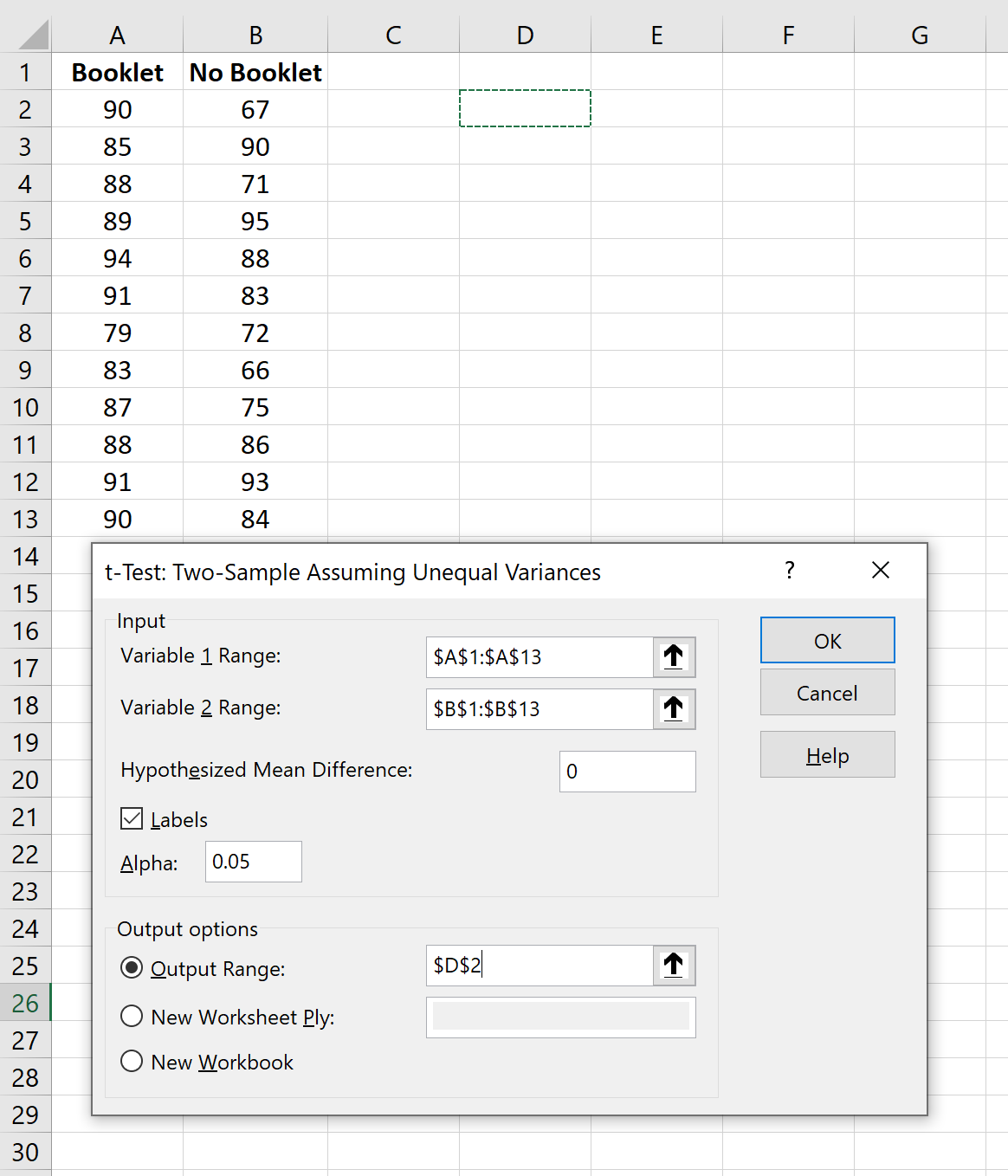
De volgende uitvoer verschijnt automatisch:

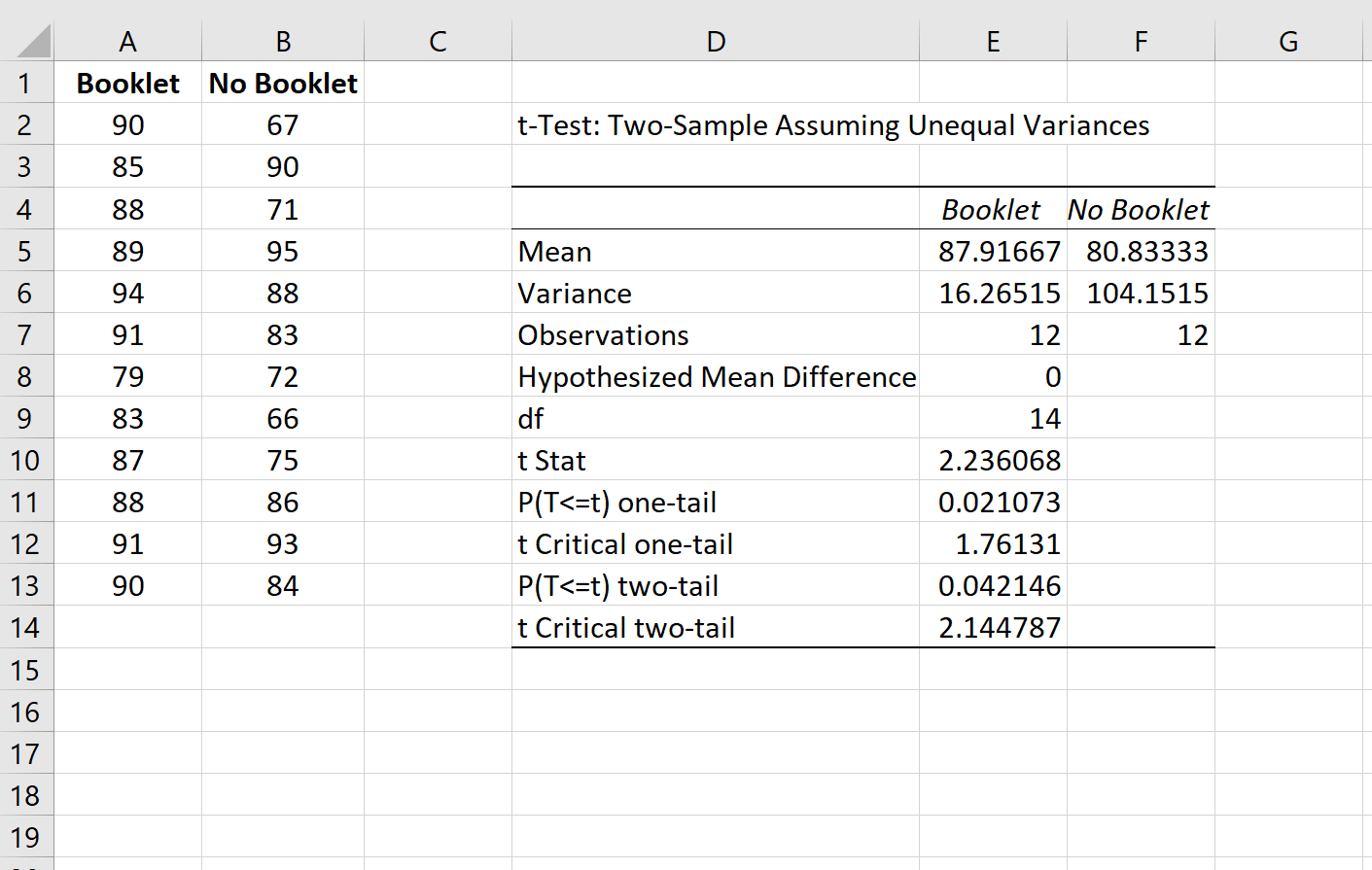
Zo interpreteert u het resultaat:

• Gemiddeld: De gemiddelde examenscore voor elke groep.
• Variantie: de variantie van examenscores per groep.
• Waarnemingen: de steekproefomvang voor elke groep.
• Hypothetisch gemiddeld verschil: gemiddeld verschil dat moet worden gebruikt in de nulhypothese van de test.
• df: De vrijheidsgraden die moeten worden gebruikt bij de teststatistiek, berekend als n ₁ + n ₂ – 2.
• t Stat: De teststatistiek voor de test.
• Eenzijdige P(T<=t): De p-waarde die is gekoppeld aan de teststatistiek voor een eenzijdige test. Negeer dit omdat we een tweezijdige test uitvoeren.
• P(T<=t) tweezijdig: p-waarde geassocieerd met de teststatistiek voor een tweezijdige test. Omdat dit minder dan 0,05 is, zouden we de nulhypothese verwerpen en concluderen dat de gemiddelde examenscore tussen de twee groepen statistisch significant verschillend is op het α = 0,05-niveau.

Stap 3: Rapporteer de resultaten.

Ten slotte willen we graag de resultaten van onze Welch’s t-test rapporteren. Hier is een voorbeeld van hoe u dit kunt doen:

Er werd een Welch’s t-test uitgevoerd om te bepalen of er een statistisch significant verschil was in examenscores tussen een groep studenten die een examenvoorbereidingsboekje gebruikten ter voorbereiding op het examen en een groep die dit niet gebruikte. De steekproefomvang voor beide groepen bedroeg 12 studenten.

Uit de t-test van Welch bleek dat er een statistisch significant verschil was in de gemiddelde examenscores (t=2,236, p=0,0421) tussen de twee groepen.