Wet van de grote getallen: definitie + voorbeelden

De wet van de grote getallen stelt dat naarmate de omvang van een steekproef toeneemt, het steekproefgemiddelde dichter bij de verwachte waarde komt.

Het eenvoudigste voorbeeld is het opgooien van een munt. Elke keer dat we een munt opgooien, is de kans dat deze kop oplevert 1/2. Het verwachte aantal kop dat zal verschijnen bij een oneindig aantal worpen is dus 1/2 of 0,5 .

Als we echter een munt tien keer opgooien, kan het zijn dat deze slechts drie keer kop oplevert. Aangezien 10 salto’s een kleine steekproefomvang is, is er geen garantie dat de kopverhouding dicht bij 0,5 zal liggen.

Als we de munt nog tien keer blijven opgooien, kan het zijn dat hij in totaal 9 van de 20 keer op kop terechtkomt. Als we hem nog eens 10 keer opgooien, komt hij misschien 22 van de 30 keer op kop terecht.

Als we de munt opgooien, zal het aantal keren dat er kop is, convergeren naar de verwachte verhouding van 0,5 .

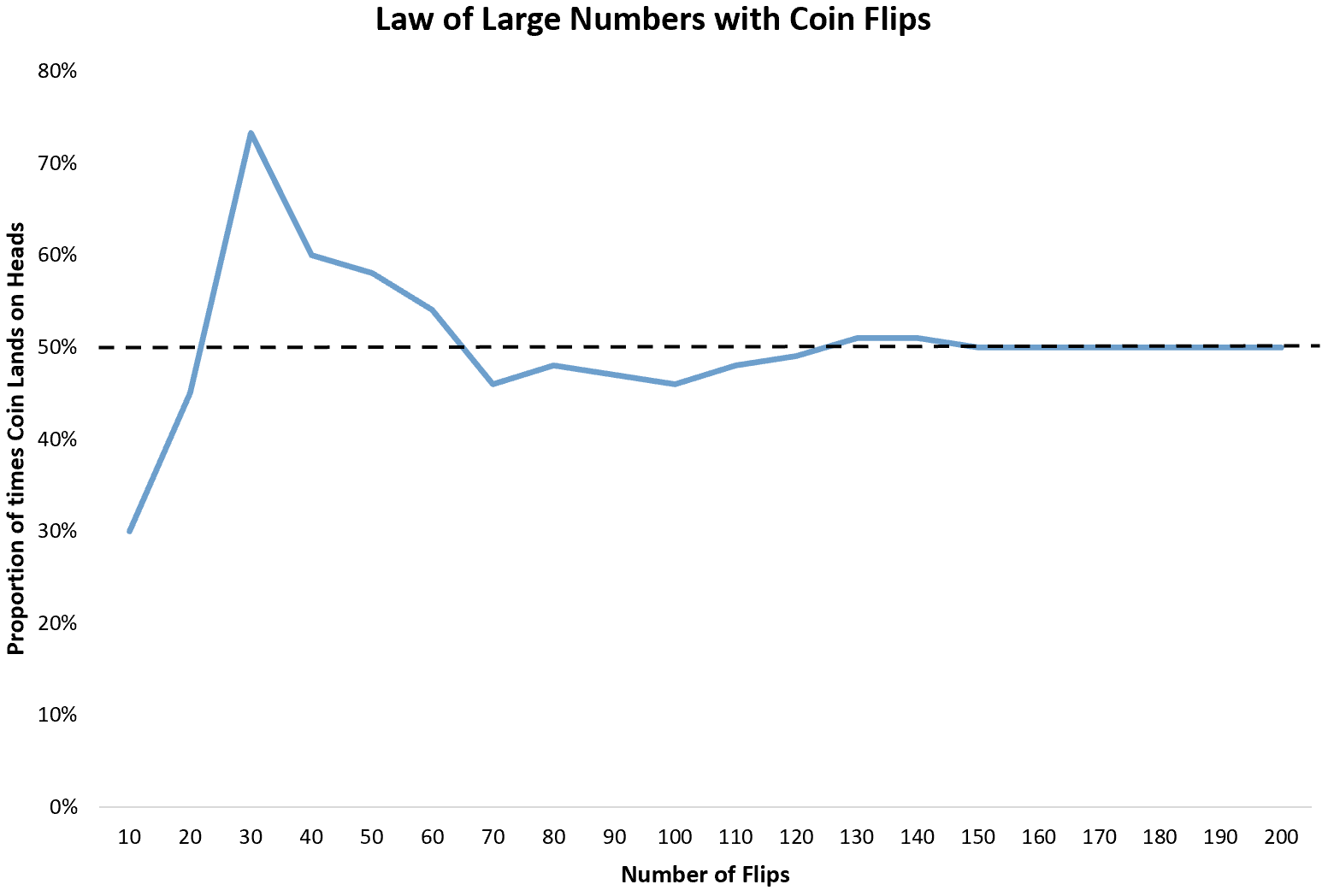
Dit eenvoudige idee van de wet van de grote getallen wordt in het echte leven door veel soorten bedrijven en industrieën toegepast.

De wet van de grote aantallen in casino’s

Casino’s vertrouwen op de wet van de grote aantallen om op betrouwbare wijze winst te genereren. Bij de meeste spellen wint het casino ongeveer 51-55% van de tijd. Dit betekent dat individuen geluk kunnen hebben en zo nu en dan een behoorlijk bedrag kunnen winnen, maar van de tienduizenden individuele spelers zal het casino de verwachte 51-55% van de tijd winnen.

Jessica zou bijvoorbeeld een paar spelletjes in het casino kunnen spelen en $ 50 winnen.

Mike kan ook een paar spelletjes spelen en $70 verliezen.

John kon een paar spelletjes spelen en $ 25 winnen.

Susan kan een paar spelletjes spelen en $ 40 verliezen.

Sommige spelers zullen geld winnen en anderen zullen geld verliezen, maar vanwege de manier waarop de spellen zijn ontworpen, kunnen casino’s er zeker van zijn dat ze uit duizenden individuen zullen winnen.

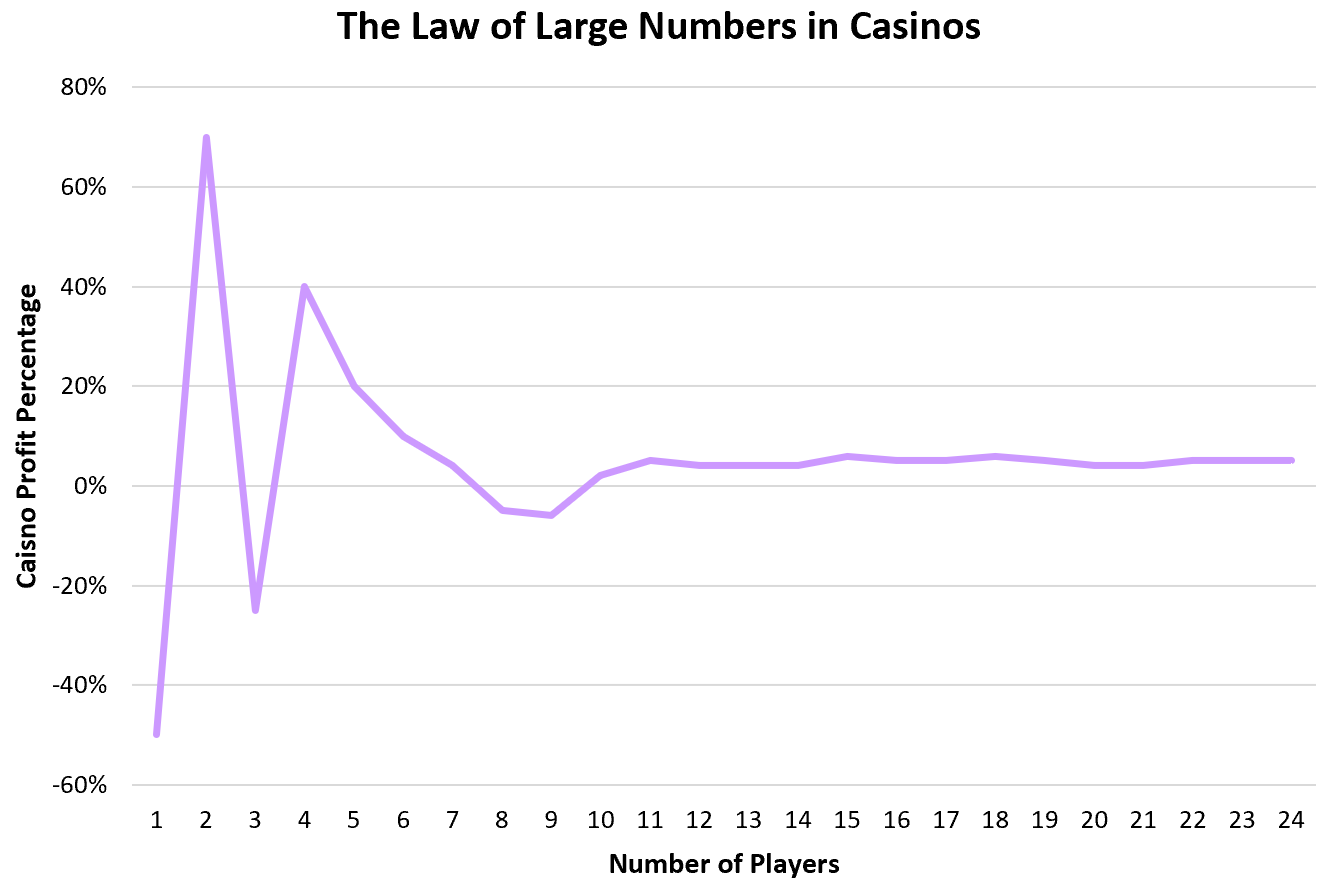
De wet van de grote aantallen in verzekeringen

Verzekeringsmaatschappijen vertrouwen ook op de wet van de grote aantallen om winstgevend te blijven.

Het basisidee is dat duizenden verzekeringsmaatschappijen een verzekering kunnen aanbieden aan mensen die maandelijks een bepaalde premie betalen en dat slechts een klein percentage van de mensen die zij verzekeren de verzekering daadwerkelijk zal moeten gebruiken om grote onverwachte uitgaven te betalen.

Bijvoorbeeld, 1.000 mensen zouden elk $1.000 per jaar kunnen betalen voor een verzekering, wat voor een verzekeringsmaatschappij een winst van $1.000.000 zou opleveren.

Het is echter mogelijk dat 90 mensen elk $10.000 van de verzekeringsmaatschappij moeten ontvangen om onverwachte kosten in verband met verschillende ongevallen te dekken, wat resulteert in een verlies van $900.000 voor de verzekeringsmaatschappij.

Uiteindelijk maakt de verzekeringsmaatschappij een winst van €1.000.000 – €900.000 = €100.000 .

Dit betekent dat de verzekeringsmaatschappij gemiddeld op duizenden mensen een redelijk voorspelbare winst kan maken.

Merk op dat dit economische model werkt omdat een verzekeringsmaatschappij een groot aantal mensen verzekert. Als ze maar tien mensen zouden verzekeren, zou het veel te riskant zijn, omdat een grote onverwachte uitgave het bedrijf zou kunnen wegvagen.

Verzekeringsmaatschappijen vertrouwen dus op de wet van de grote aantallen om hun winsten op een voorspelbare manier te voorspellen.

De wet van de grote aantallen in hernieuwbare energieën

De wet van de grote aantallen wordt ook gebruikt door duurzame energiebedrijven.

Het basisidee is dat windturbines en zonnepanelen generatoren kunnen aandrijven om elektriciteit te produceren in verschillende delen van het bedrijf. Buiten is er echter geen wind of zon, waardoor windturbines en zonnepanelen niet altijd betrouwbare stroom kunnen produceren voor elektrische generatoren.

De manier waarop duurzame energiebedrijven dit probleem omzeilen, is door tienduizenden windturbines of zonnepanelen op één elektriciteitsnet aan te sluiten, waardoor het veel waarschijnlijker wordt dat deze energiebronnen een betrouwbare hoeveelheid energie zullen produceren. energie voor het netwerk.

Het is ook veel gemakkelijker om te voorspellen hoeveel energie door deze energiebronnen zal worden geproduceerd, omdat ingenieurs eenvoudigweg het verwachte gemiddelde van tienduizenden windturbines of zonnepanelen kunnen nemen.

Een gedetailleerde uitleg van dit fenomeen is te vinden in dit Scientific American-artikel .