Hoe u de door wilcoxon ondertekende rangtest uitvoert

De door Wilcoxon ondertekende rangtest is de niet-parametrische versie van de gepaarde t-test . Het wordt gebruikt om te testen of er al dan niet een significant verschil bestaat tussen twee populatiegemiddelden.

Wanneer moet u de door Wilcoxon ondertekende rangtest gebruiken?

Gebruik de Wilcoxon Signed Rank-test als u de gepaarde t-test wilt gebruiken, maar de verdeling van de verschillen tussen paren ernstig niet-normaal verdeeld is.

De eenvoudigste manier om te bepalen of de verschillen niet normaal verdeeld zijn, is door een histogram van de verschillen te maken en te kijken of ze een enigszins normale, „klokvormige“ verdeling volgen.

Houd er rekening mee dat de gepaarde t-test behoorlijk robuust is voor afwijkingen van de normaliteit, dus de afwijking van een normale verdeling moet groot genoeg zijn om het gebruik van de Wilcoxon Signed Rank-test te rechtvaardigen.

Hoe u de door Wilcoxon ondertekende rangtest kunt afleggen

Het volgende voorbeeld illustreert hoe u de Wilcoxon Signed Rank-test uitvoert.

Een basketbalcoach wil weten of een bepaald trainingsprogramma het aantal vrije worpen van zijn spelers doet toenemen. Om dit te testen vroeg hij 15 spelers om voor en na het trainingsprogramma elk 20 vrije worpen te maken.

Omdat elke speler aan zichzelf kan worden ‚gekoppeld‘, was de coach van plan een gepaarde t-test te gebruiken om te bepalen of er een significant verschil was tussen het gemiddelde aantal vrije worpen dat voor en na het trainingsprogramma werd gemaakt. opleiding.

De verdeling van de verschillen blijkt echter niet normaal te zijn, en daarom gebruikt de coach in plaats daarvan een door Wilcoxon ondertekende rangtest.

De volgende tabel toont het aantal gemaakte vrije worpen (van de 20 pogingen) door elk van de 15 spelers, voor en na het trainingsprogramma:

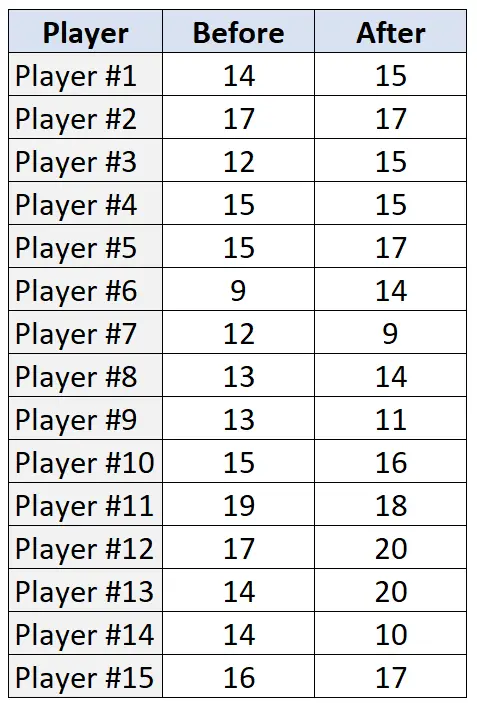
Stap 1: Formuleer de nul- en alternatieve hypothesen.

H ₀ : Het gemiddelde verschil tussen de twee groepen is nul.

H _A : Het mediaanverschil is negatief. (spelers maken bijvoorbeeld minder vrije worpen voordat ze deelnemen aan het trainingsprogramma)

Stap 2: Zoek het verschil en het absolute verschil voor elk paar.

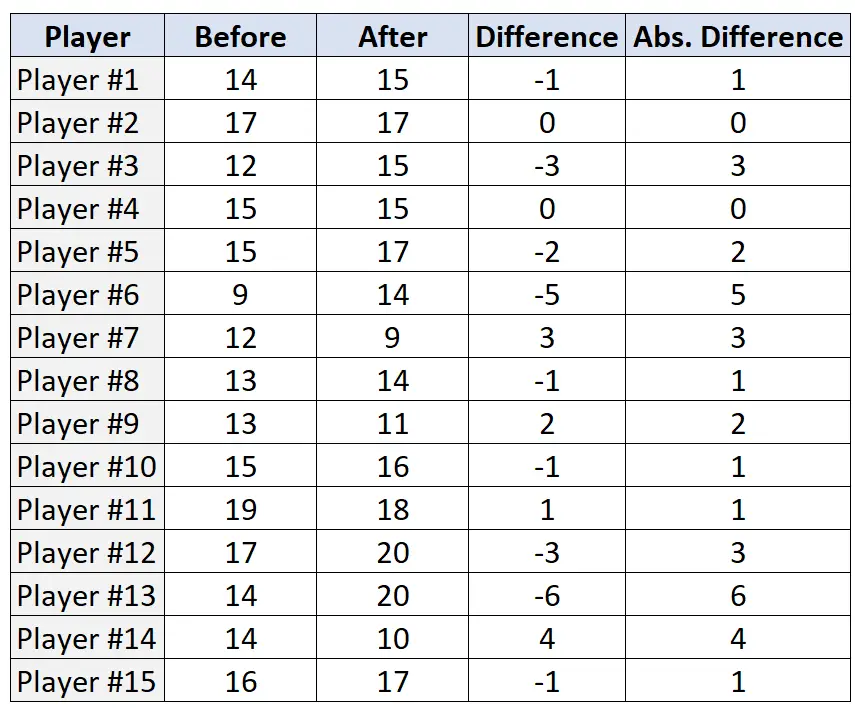
Stap 3: Rangschik de paren op basis van absolute verschillen en wijs een rang toe van het kleinste naar het grootste absolute verschil. Negeer paren met een absoluut verschil van „0“ en wijs gemiddelde rangen toe in geval van een gelijkspel.

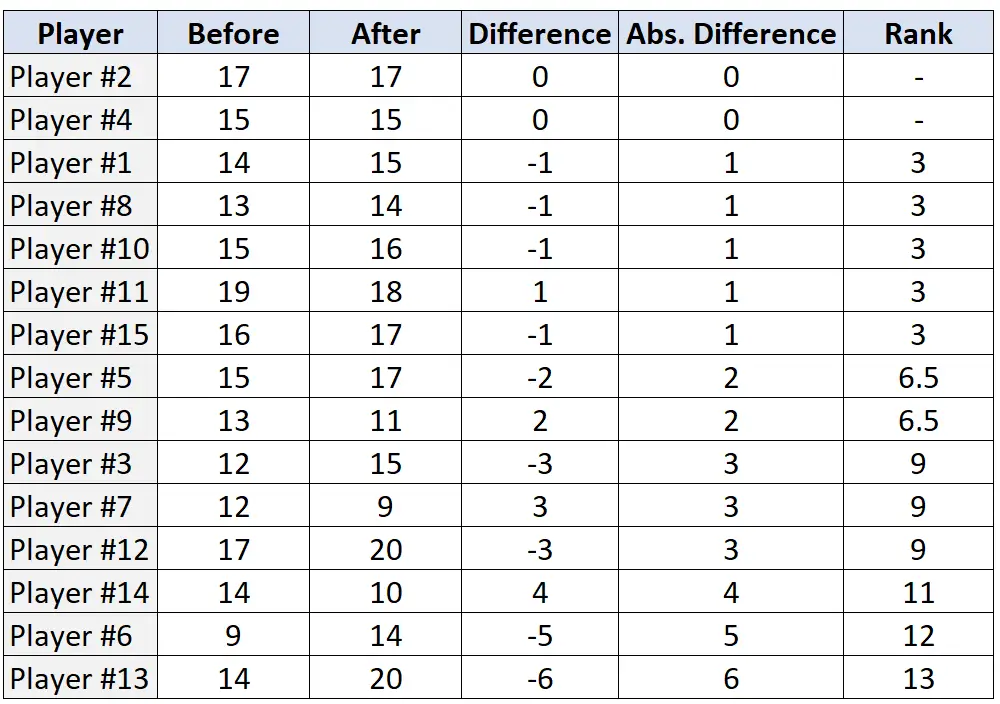
Stap 4: Vind de som van positieve rangen en negatieve rangen.

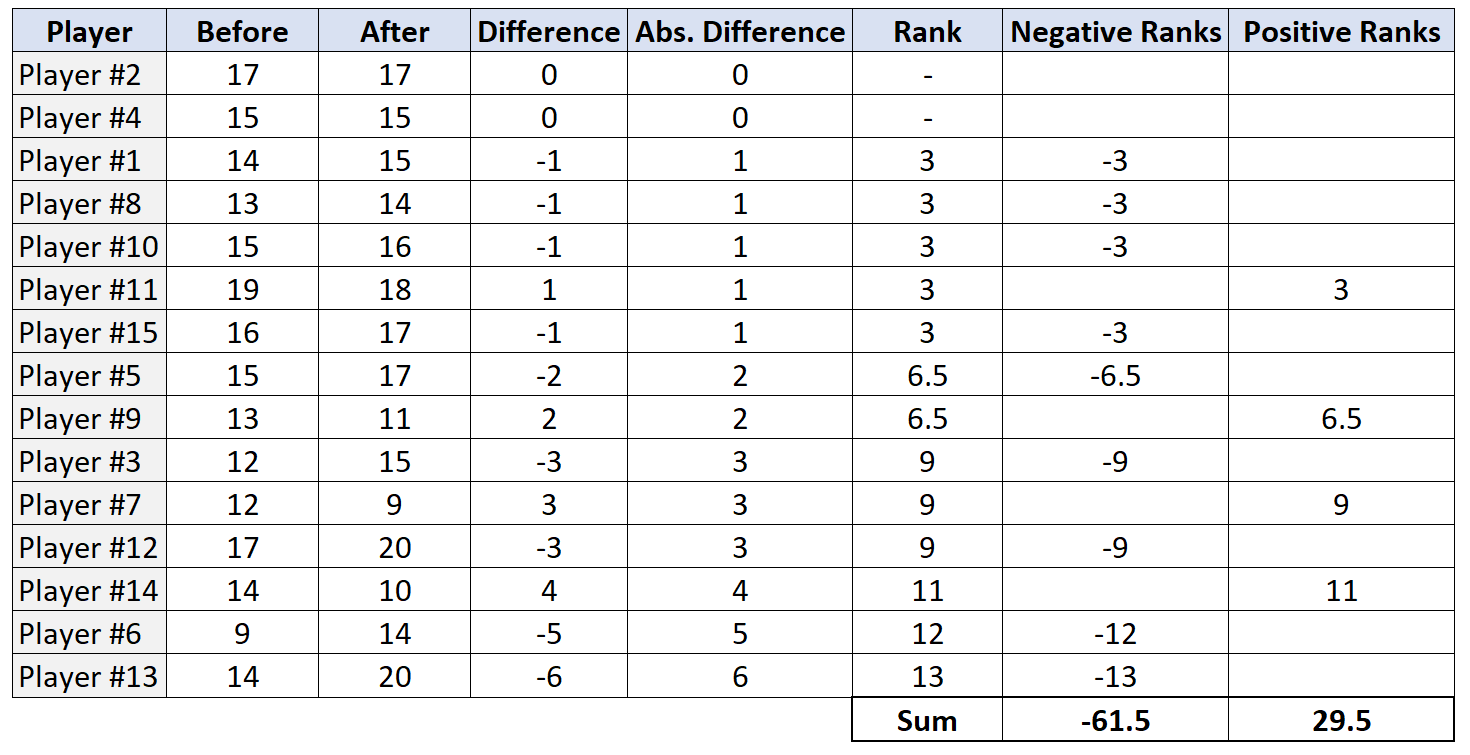
Stap 5: Verwerp de nulhypothese of verwerp deze niet.

De teststatistiek, W, is de kleinste van de absolute waarden van de positieve rangen en de negatieve rangen. In dit geval is de kleinste waarde 29,5. Onze teststatistiek is dus W = 29,5 .

Om te bepalen of we de nulhypothese wel of niet moeten verwerpen, kunnen we verwijzen naar de kritische waarde in de door Wilcoxon ondertekende ranglijst met kritische waarden die overeenkomt met n en het gekozen alfaniveau.

Als onze teststatistiek, W, kleiner is dan of gelijk is aan de kritische waarde in de tabel, kunnen we de nulhypothese verwerpen. Anders zullen we er niet in slagen de nulhypothese te verwerpen.

De kritische waarde die overeenkomt met een alfaniveau van 0,05 en n = 13 (het totale aantal paren minus de twee waarvoor we geen rangschikking hebben berekend omdat ze een waargenomen verschil van 0 hadden) is 17 .

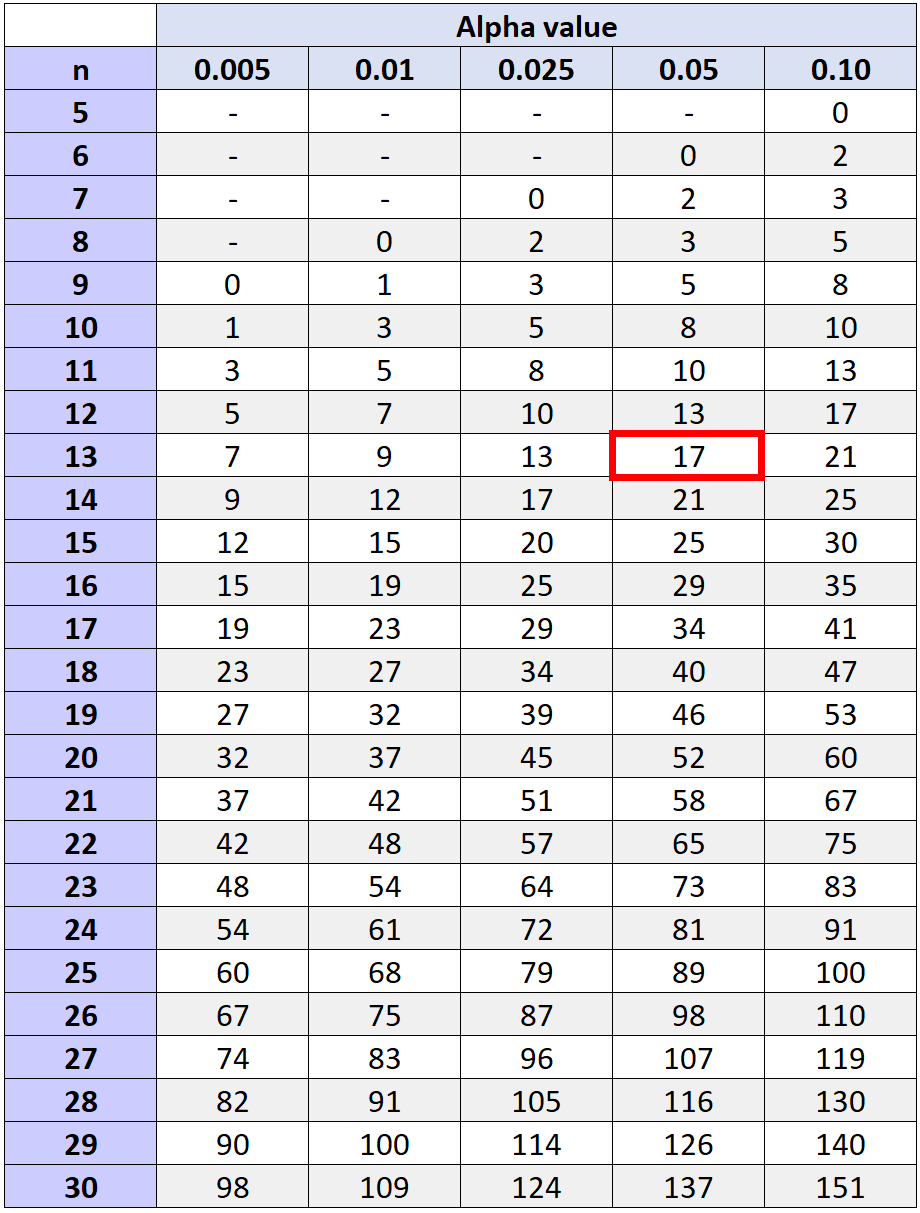
Omdat onze teststatistiek (W = 29,5) niet kleiner is dan of gelijk is aan 17, slagen we er niet in de nulhypothese te verwerpen. We hebben onvoldoende bewijs om te zeggen dat het trainingsprogramma resulteert in een significante toename van het aantal vrije worpen dat door spelers wordt gemaakt.

Opmerking: Gebruik de Wilcoxon Signed Rank Test Calculator als u de test met een rekenmachine wilt uitvoeren in plaats van met de hand.