Hoe de wilcoxon ondertekende rangtest uit te voeren in r

De Wilcoxon Signed-Rank-test is de niet-parametrische versie van de gepaarde t-test . Het wordt gebruikt om te testen of er al dan niet een significant verschil bestaat tussen de gemiddelden van twee populaties wanneer de verdeling van de verschillen tussen de twee steekproeven niet als normaal kan worden beschouwd.

In deze tutorial wordt uitgelegd hoe u een door Wilcoxon ondertekende rangtest uitvoert in R.

Voorbeeld: Wilcoxon ondertekende rangtest in R

Stel dat een basketbalcoach wil weten of een bepaald trainingsprogramma het aantal vrije worpen van zijn spelers doet toenemen. Om dit te testen vroeg hij 15 spelers om voor en na het trainingsprogramma elk 20 vrije worpen te maken.

Omdat elke speler aan zichzelf kan worden ‚gekoppeld‘, was de coach van plan een gepaarde t-test te gebruiken om te bepalen of er een significant verschil was tussen het gemiddelde aantal vrije worpen dat voor en na het trainingsprogramma werd gemaakt. opleiding. De verdeling van de verschillen blijkt echter niet normaal te zijn, daarom gebruikt de trainer in plaats daarvan een Wilcoxon Signed-Rank test.

De volgende tabel toont het aantal gemaakte vrije worpen (van de 20 pogingen) door elk van de 15 spelers, voor en na het trainingsprogramma:

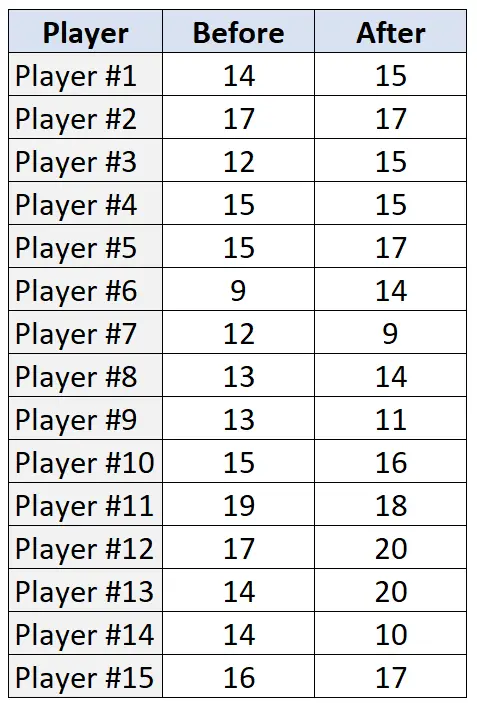
Om de Wilcoxon Signed-Rank Test uit te voeren op deze gegevens in R, kunnen we de functie wilcox.test() gebruiken, die de volgende syntaxis gebruikt:

wilcox.test(x, y, even = WAAR)

Goud:

• x, y: twee vectoren van gegevenswaarden
• gepaard: als u dit op TRUE instelt, vertelt R dat onze twee vectoren gepaarde gegevens bevatten

De volgende code laat zien hoe u deze functie kunt gebruiken om de Wilcoxon Signed-Rank-test op deze gegevens uit te voeren:

 #create the two vectors of data
before <- c(14, 17, 12, 15, 15, 9, 12, 13, 13, 15, 19, 17, 14, 14, 16)
after <- c(15, 17, 15, 15, 17, 14, 9, 14, 11, 16, 18, 20, 20, 10, 17)

#perform Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE)

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.275
alternative hypothesis: true location shift is not equal to 0

De teststatistiek is 29,5 en de overeenkomstige p-waarde is 0,275 . Omdat deze p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen. Er was geen statistisch significant verschil in het aantal vrije worpen voor en na deelname van de spelers aan het trainingsprogramma.

Standaard voert deze functie een tweezijdige Wilcoxon Signed-Rank-test uit, maar u kunt een linkshandige of een rechtshandige test opgeven met behulp van het alternatieve argument:

 #perform left-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="less")

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.1375
alternative hypothesis: true location shift is less than 0

#perform right-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="greater")

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.8774
alternative hypothesis: true location shift is greater than 0

Aanvullende bronnen

Een inleiding tot de door Wilcoxon ondertekende rangtest
Wilcoxon ondertekende plaatstestcalculator