Willekeurige bossen maken in r (stap voor stap)

Wanneer de relatie tussen een reeks voorspellende variabelen en een responsvariabele erg complex is, gebruiken we vaak niet-lineaire methoden om de relatie daartussen te modelleren.

Eén zo’n methode is het bouwen van een beslisboom . Het nadeel van het gebruik van één enkele beslissingsboom is echter dat deze vaak te kampen heeft met een hoge variantie .

Dat wil zeggen: als we de dataset in twee helften splitsen en de beslissingsboom op beide helften toepassen, kunnen de resultaten heel verschillend zijn.

Eén methode die we kunnen gebruiken om de variantie van een enkele beslissingsboom te verkleinen, is door een willekeurig bosmodel te bouwen, dat als volgt werkt:

1. Neem b- bootstrapped samples uit de originele dataset.

2. Maak een beslissingsboom voor elk bootstrap-voorbeeld.

• Bij het construeren van de boom wordt elke keer dat een splitsing wordt overwogen, slechts een willekeurige steekproef van m- voorspellers beschouwd als kandidaten voor splitsing uit de volledige set van p- voorspellers. Over het algemeen kiezen we m gelijk aan √p .

3. Gemiddelde van de voorspellingen van elke boom om een definitief model te verkrijgen.

Het blijkt dat willekeurige bossen de neiging hebben om veel nauwkeurigere modellen te produceren dan afzonderlijke beslissingsbomen en zelfs modellen in zakken .

Deze zelfstudie biedt een stapsgewijs voorbeeld van hoe u een willekeurig forest-model maakt voor een gegevensset in R.

Stap 1: Laad de benodigde pakketten

Eerst laden we de benodigde pakketten voor dit voorbeeld. Voor dit eenvoudige voorbeeld hebben we slechts één pakket nodig:

 library (randomForest)

Stap 2: Pas het willekeurige bosmodel aan

Voor dit voorbeeld gebruiken we een ingebouwde R-dataset genaamd Air Quality , die metingen bevat van de luchtkwaliteit in New York City gedurende 153 afzonderlijke dagen.

 #view structure of air quality dataset
str(airquality)

'data.frame': 153 obs. of 6 variables:
 $ Ozone: int 41 36 12 18 NA 28 23 19 8 NA ...
 $Solar.R: int 190 118 149 313 NA NA 299 99 19 194 ...
 $ Wind: num 7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ...
 $ Temp: int 67 72 74 62 56 66 65 59 61 69 ...
 $Month: int 5 5 5 5 5 5 5 5 5 5 ...
 $Day: int 1 2 3 4 5 6 7 8 9 10 ...

#find number of rows with missing values
sum(! complete . cases (airquality))

[1] 42

Deze gegevensset bevat 42 rijen met ontbrekende waarden. Voordat we een willekeurig bosmodel fitten, zullen we daarom de ontbrekende waarden in elke kolom invullen met de kolommedianen:

 #replace NAs with column medians
for (i in 1: ncol (air quality)) {
  airquality[,i][ is . na (airquality[, i])] <- median (airquality[, i], na . rm = TRUE )
}

Gerelateerd: Hoe ontbrekende waarden toe te schrijven aan R

De volgende code laat zien hoe u een willekeurig forest-model in R kunt passen met behulp van de functie randomForest() uit het pakket randomForest .

 #make this example reproducible
set.seed(1)

#fit the random forest model
model <- randomForest(
  formula = Ozone ~ .,
  data = airquality
)

#display fitted model
model

Call:
 randomForest(formula = Ozone ~ ., data = airquality) 
               Type of random forest: regression
                     Number of trees: 500
No. of variables tried at each split: 1

          Mean of squared residuals: 327.0914
                    % Var explained: 61

#find number of trees that produce lowest test MSE
which.min(model$mse)

[1] 82

#find RMSE of best model
sqrt(model$mse[ which . min (model$mse)]) 

[1] 17.64392

Uit het resultaat kunnen we zien dat het model dat de laagste gemiddelde kwadratische fout (MSE) produceerde, 82 bomen gebruikte.

We kunnen ook zien dat de root mean square error van dit model 17,64392 was. We kunnen dit beschouwen als het gemiddelde verschil tussen de voorspelde waarde voor ozon en de daadwerkelijk waargenomen waarde.

We kunnen ook de volgende code gebruiken om een plot van de MSE-test te maken op basis van het aantal gebruikte bomen:

 #plot the MSE test by number of trees
plot(model)

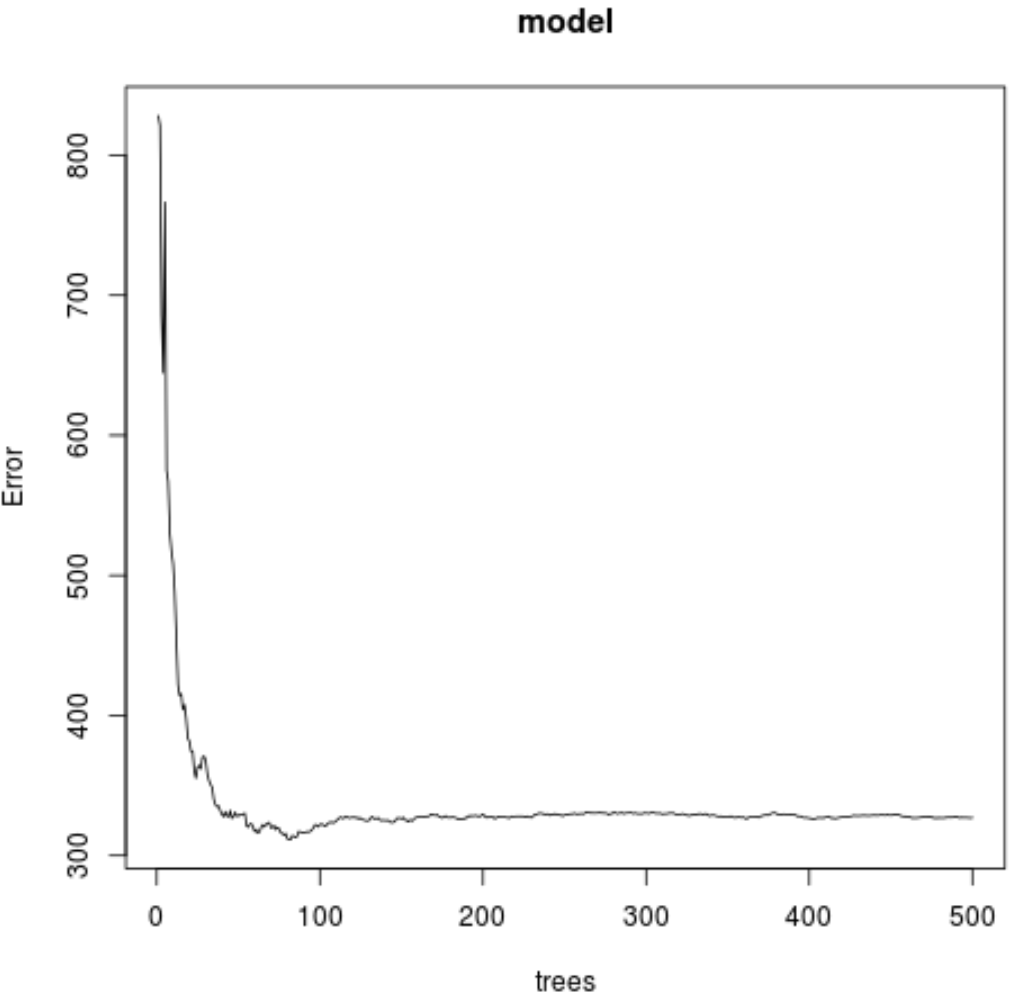
En we kunnen de functie varImpPlot() gebruiken om een plot te maken die het belang van elke voorspellende variabele in het uiteindelijke model weergeeft:

 #produce variable importance plot
varImpPlot(model) 

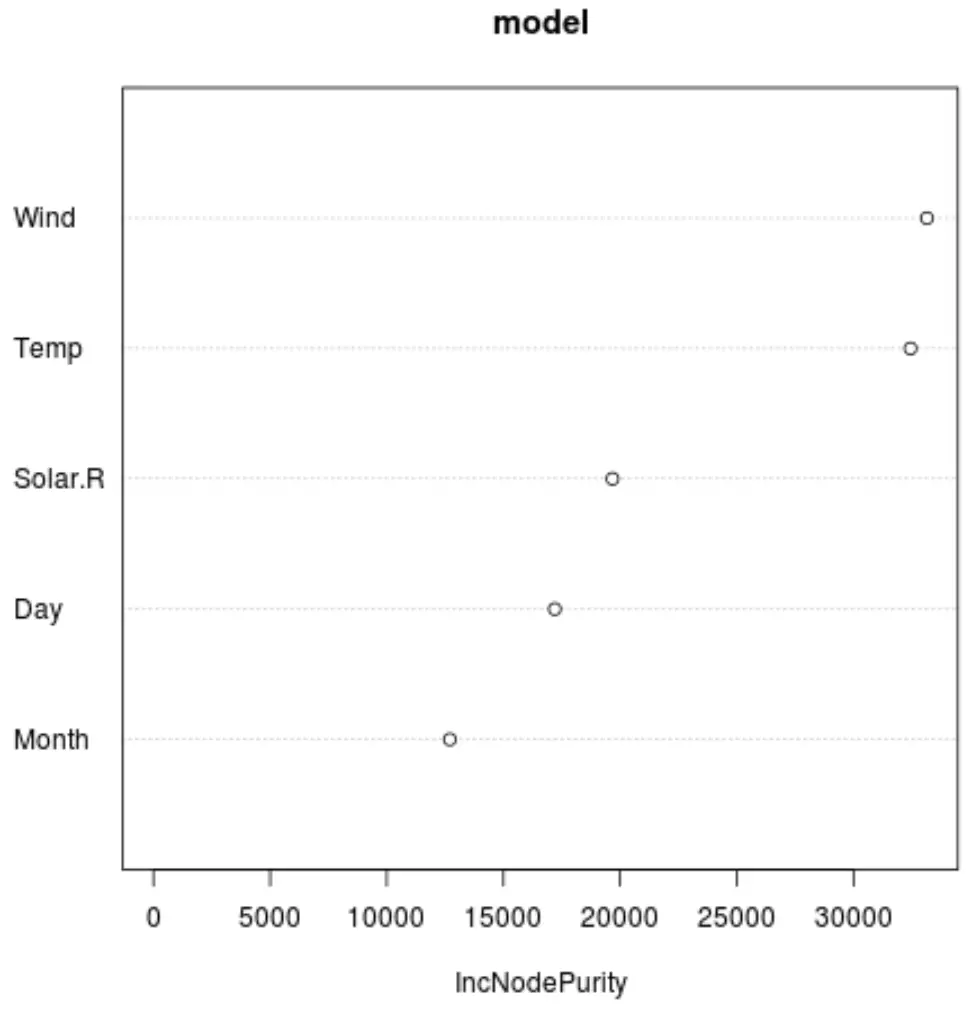
Op de x-as wordt de gemiddelde toename in knooppuntzuiverheid van de regressiebomen weergegeven als functie van de splitsing over de verschillende voorspellers die op de y-as worden weergegeven.

Uit de grafiek kunnen we zien dat Wind de belangrijkste voorspellende variabele is, op de voet gevolgd door Temp .

Stap 3: Pas het model aan

Standaard gebruikt de functie randomForest() 500 bomen en (totaal voorspellers/3) willekeurig geselecteerde voorspellers als potentiële kandidaten voor elke splitsing. We kunnen deze parameters aanpassen met behulp van de tuneRF() functie.

De volgende code laat zien hoe u het optimale model kunt vinden met behulp van de volgende specificaties:

• ntreeTry: Het aantal bomen dat moet worden gebouwd.
• mtryStart: het aanvankelijke aantal voorspellende variabelen waarmee bij elke divisie rekening moet worden gehouden.
• stepFactor: Factor die moet worden verhoogd totdat de geschatte out-of-bag-fout niet meer met een bepaald bedrag verbetert.
• verbeteren: de hoeveelheid waarmee de fout bij het verlaten van de zak moet worden verbeterd om de stapfactor te blijven verhogen.

 model_tuned <- tuneRF(
               x=airquality[,-1], #define predictor variables
               y=airquality$Ozone, #define response variable
               ntreeTry= 500 ,
               mtryStart= 4 , 
               stepFactor= 1.5 ,
               improve= 0.01 ,
               trace= FALSE #don't show real-time progress
               )

Deze functie produceert de volgende grafiek, die het aantal voorspellers weergeeft dat bij elke splitsing wordt gebruikt bij het construeren van de bomen op de x-as en de geschatte out-of-bag-fout op de y-as:

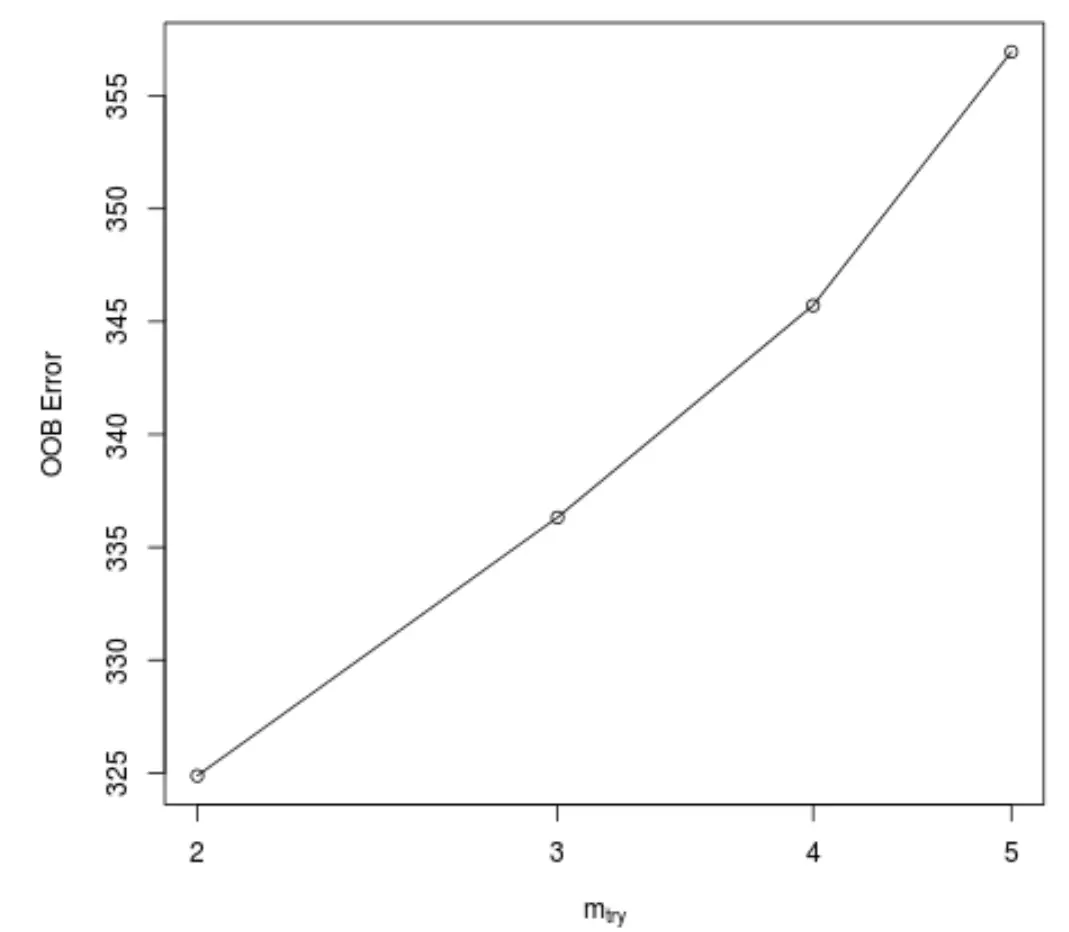
We kunnen zien dat de laagste OOB-fout wordt verkregen door bij elke splitsing twee willekeurig gekozen voorspellers te gebruiken bij het bouwen van de bomen.

Dit komt feitelijk overeen met de standaardinstelling (totale voorspellers/3 = 6/3 = 2) die wordt gebruikt door de initiële functie randomForest() .

Stap 4: Gebruik het definitieve model om voorspellingen te doen

Ten slotte kunnen we het aangepaste willekeurige bosmodel gebruiken om voorspellingen te doen over nieuwe waarnemingen.

 #define new observation
new <- data.frame(Solar.R=150, Wind=8, Temp=70, Month=5, Day=5)

#use fitted bagged model to predict Ozone value of new observation
predict(model, newdata=new)

27.19442

Op basis van de waarden van de voorspellende variabelen voorspelt het gepaste willekeurige bosmodel dat de ozonwaarde op deze specifieke dag 27,19442 zal zijn.

De volledige R-code die in dit voorbeeld wordt gebruikt, vindt u hier .