Wat zijn willekeurige variabelen?

Een willekeurige variabele , doorgaans aangeduid met X, is een variabele waarvan de mogelijke waarden het resultaat zijn van een willekeurig proces.

Er zijn twee soorten willekeurige variabelen: discreet en continu .

Discrete willekeurige variabelen

Een discrete willekeurige variabele is er een die slechts een telbaar aantal verschillende waarden kan aannemen, zoals 0, 1, 2, 3, 4, 5…100, 1 miljoen, enz. Hier zijn enkele voorbeelden van discrete willekeurige variabelen:

• Het aantal keren dat een munt munt krijgt nadat hij twintig keer is gegooid.
• Het aantal keren dat een dobbelsteen op nummer 4 belandt nadat hij 100 keer is gegooid.
• Het aantal defecte widgets in een doos van 50 widgets.

Een kansverdeling voor een discrete willekeurige variabele vertelt ons de waarschijnlijkheid dat de willekeurige variabele bepaalde waarden aanneemt.

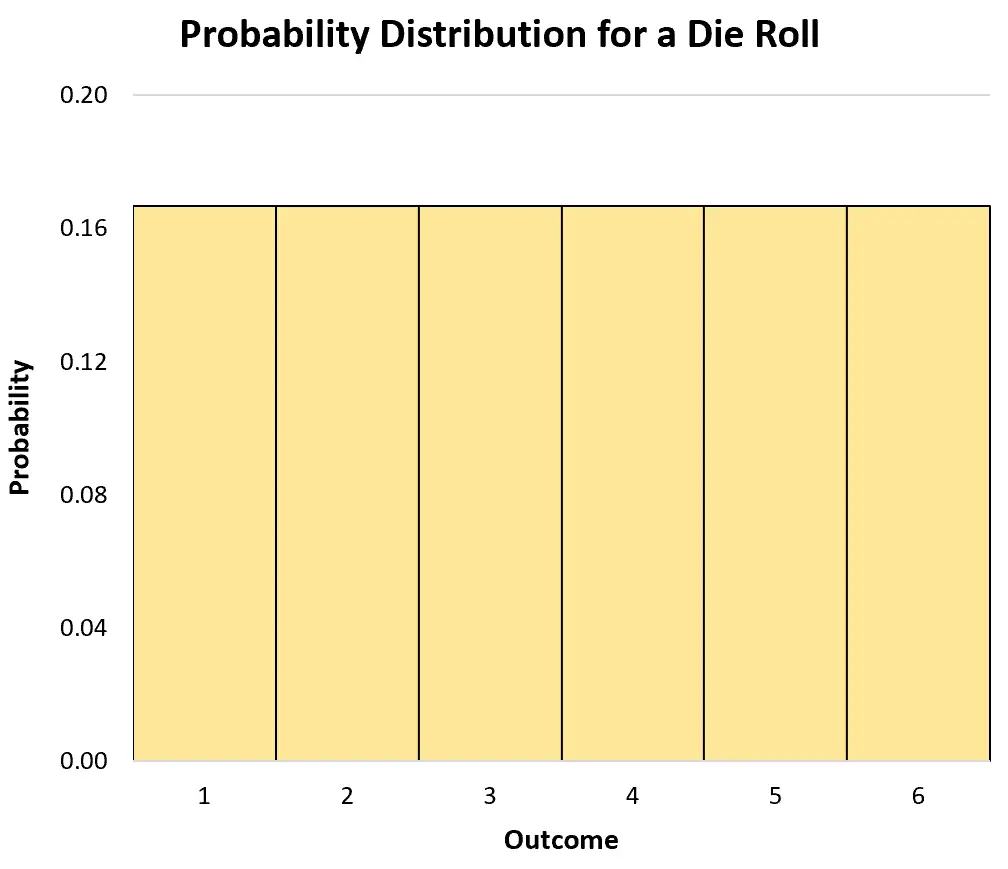
Stel bijvoorbeeld dat we één keer met een eerlijke dobbelsteen gooien. Als we X de kans laten aangeven dat de dobbelsteen op een bepaald getal valt, dan kan de kansverdeling als volgt worden geschreven:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

Opmerking:

Wil een kansverdeling geldig zijn, dan moet deze aan de volgende twee criteria voldoen:

1. De waarschijnlijkheid van elke uitkomst moet tussen 0 en 1 liggen.

2. De som van alle kansen moet opgeteld 1 zijn.

Merk op dat de kansverdeling voor de dobbelsteenworp aan beide criteria voldoet:

1. De waarschijnlijkheid van elke uitkomst ligt tussen 0 en 1.

2. De som van alle kansen is opgeteld 1.

We kunnen een histogram gebruiken om de waarschijnlijkheidsverdeling te visualiseren:

Een cumulatieve waarschijnlijkheidsverdeling voor een discrete willekeurige variabele vertelt ons de waarschijnlijkheid dat de variabele een waarde aanneemt die gelijk is aan of kleiner is dan een bepaalde waarde.

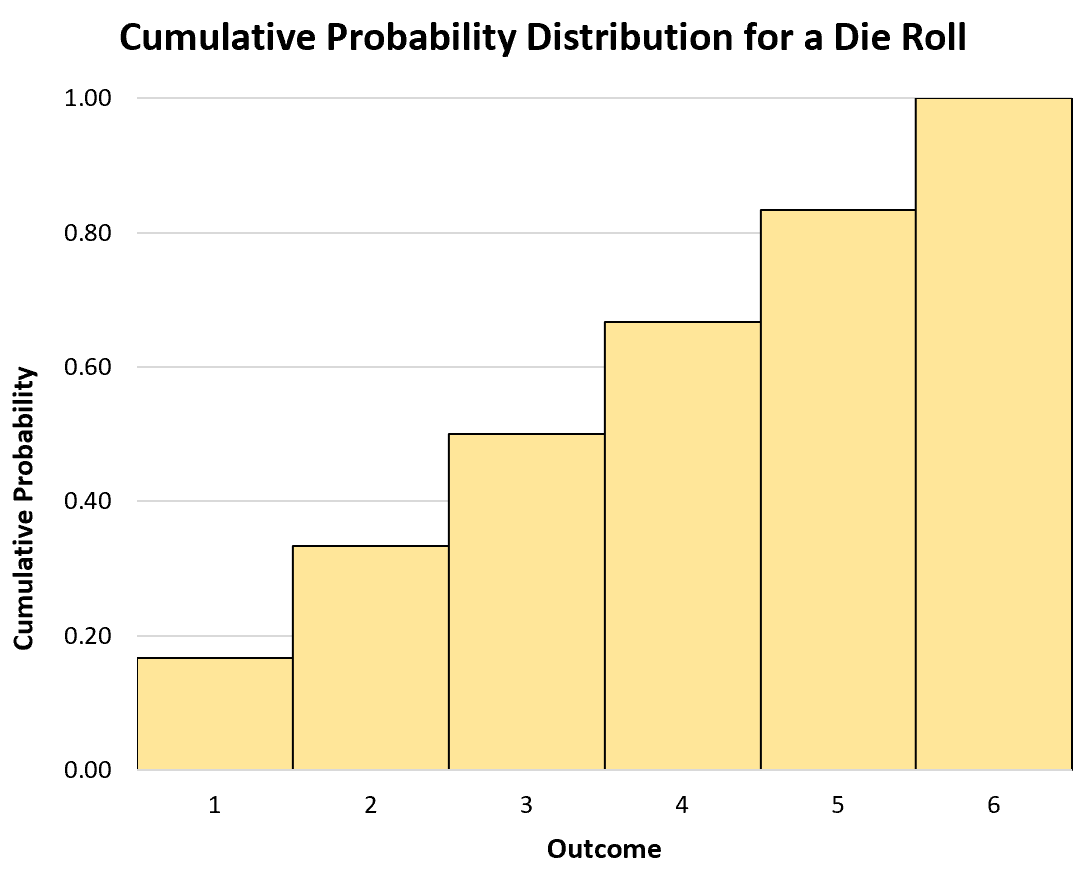
De cumulatieve kansverdeling voor een dobbelsteenworp zou er bijvoorbeeld als volgt uitzien:

• P(X≤1): 1/6
• P(X≤2): 2/6
• P(X≤3): 3/6
• P(X≤4): 4/6
• P(X≤5): 5/6
• P(X≤6): 6/6

De kans dat de dobbelsteen op één of minder terechtkomt is eenvoudigweg 1/6, aangezien deze niet op een getal kleiner dan één kan landen.

De kans dat het op twee of minder landt, is P(X=1) + P(X=2) = 1/6 + 1/6 = 2/6.

Op dezelfde manier is de kans dat het op drie of minder landt P(X=1) + P(X=2) + P(X=3) = 1/6 + 1/6 + 1/6 = 3/6, En spoedig.

We kunnen ook een histogram gebruiken om de cumulatieve waarschijnlijkheidsverdeling te visualiseren:

Continue willekeurige variabelen

Een continue willekeurige variabele is een variabele die oneindig veel mogelijke waarden kan aannemen. Hier zijn enkele voorbeelden van continue willekeurige variabelen:

• Gewicht van een dier
• Hoogte van een persoon
• Tijd die nodig is om een marathon te lopen

De lengte van een persoon kan bijvoorbeeld 60,2 inch, 65,2344 inch, 70,431222 inch, enz. Zijn. Er zijn oneindig veel mogelijke waarden voor grootte.

Algemene regel:

Als je het aantal uitkomsten kunt tellen , dan werk je met een discrete willekeurige variabele, bijvoorbeeld door het aantal keren te tellen dat een munt kop oplevert.

Maar als je de uitkomst kunt meten , werk je met een continue willekeurige variabele, bijvoorbeeld het meten van lengte, gewicht, tijd, enz.

Een kansverdeling voor een continue willekeurige variabele vertelt ons de waarschijnlijkheid dat de willekeurige variabele bepaalde waarden aanneemt.

In tegenstelling tot een waarschijnlijkheidsverdeling voor discrete willekeurige variabelen kan een waarschijnlijkheidsverdeling voor een continue willekeurige variabele echter alleen worden gebruikt om ons de waarschijnlijkheid te vertellen dat de variabele een reeks waarden aanneemt.

Stel dat we bijvoorbeeld de waarschijnlijkheid willen weten dat een hamburger van een bepaald restaurant een kwart pond (0,25 pond) weegt. Omdat gewicht een continue variabele is, kan het een oneindig aantal waarden aannemen.

Een bepaalde hamburger kan bijvoorbeeld in werkelijkheid 0,250001 pond wegen, of 0,24 pond, of 0,2488 pond. De kans dat een bepaalde hamburger precies 0,25 pond weegt, is in wezen nul.

We kunnen dus alleen een kansverdeling gebruiken om ons de waarschijnlijkheid te vertellen dat een hamburger minder dan 0,25 kg weegt, meer dan 0,25 kg, of binnen een bepaald bereik ligt (bijvoorbeeld tussen 0,23 kg en 0,27 kg).

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over willekeurige variabelen:

Wat zijn iid willekeurige variabelen?
10 voorbeelden van willekeurige variabelen in het echte leven