Yate continuïteitscorrectie: definitie en voorbeeld

Een chikwadraattest voor onafhankelijkheid wordt gebruikt om te bepalen of er al dan niet een significant verband bestaat tussen twee categorische variabelen.

Deze test maakt gebruik van de volgende nul- en alternatieve hypothesen:

• H ₀ : (nulhypothese) De twee variabelen zijn onafhankelijk.
• H ₁ : (alternatieve hypothese) De twee variabelen zijn niet onafhankelijk. (dwz ze zijn geassocieerd)

We gebruiken de volgende formule om de Chi-kwadraat x ^2- teststatistiek voor deze test te berekenen:

X ² = Σ(O _ik -E _ik ) ² / E _ik

Goud:

• Σ: is een mooi symbool dat “som” betekent
• O: waargenomen waarde
• E: verwachte waarde

Bij deze test wordt ervan uitgegaan dat de discrete waarschijnlijkheden van frequenties in een kruistabel kunnen worden benaderd door de Chi-kwadraatverdeling, die een continue verdeling is.

Deze veronderstelling is echter meestal enigszins onjuist en de resulterende teststatistieken zijn doorgaans opwaarts gericht.

Om voor deze vertekening te corrigeren, kunnen we de continuïteitscorrectie van Yate toepassen, die de volgende correctie toepast op de formule ^X2 :

X ² = Σ(|O _ik -E _ik | – 0,5) ² / E _ik

Over het algemeen gebruiken we deze correctie alleen als ten minste één cel in de kruistabel een verwachte frequentie van minder dan 5 heeft.

Voorbeeld: toepassing van de continuïteitscorrectie van Yate

Stel dat we willen weten of gender wel of niet geassocieerd is met de voorkeur voor een politieke partij. We nemen een eenvoudige willekeurige steekproef van 40 kiezers en vragen hen naar hun politieke partijvoorkeur. De volgende tabel geeft de resultaten van het onderzoek weer:

Hier ziet u hoe u een chi-kwadraattest van onafhankelijkheid uitvoert met de continuïteitscorrectie van Yate:

Waargenomen waarden:

Verwachte waarden:

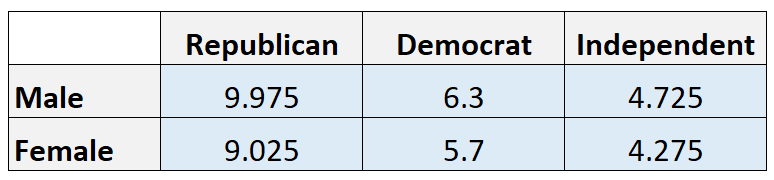
Opmerking: We berekenen de verwachte waarde in elke cel door het rijtotaal te vermenigvuldigen met het kolomtotaal en vervolgens te delen door het eindtotaal. Het verwachte aantal Republikeinse mannen is bijvoorbeeld (21*19)/40 = 9,975.

^{Chi –} _{kwadraatteststatistiek : _} _

• (|8-9,975| – 0,5) ² / 9,975 = 0,218
• (|9-6,3| – 0,5) ² / 6,3 = 0,768
• (|4-4,725| – 0,5) ² / 4,725 = 0,011
• (|11-9,025| – 0,5) ² / 9,025 = 0,241
• (|3-5,7| – 0,5) ² / 5,7 = 0,849
• (|5-4,275| – 0,5) ² / 4,275 = 0,012

^Dus ,

P-waarde: Volgens dechikwadraat-naar-p-waardecalculator is de p-waarde die overeenkomt met een chikwadraatteststatistiek met 2 vrijheidsgraden 0,3501 .

Omdat deze p-waarde niet kleiner is dan 0,05, zullen we er niet in slagen de nulhypothese te verwerpen. Dit betekent dat we niet voldoende bewijs hebben om te zeggen dat er een verband bestaat tussen geslacht en politieke partijvoorkeuren.