Hoe u de kritische z-waarde kunt vinden op een ti-84-rekenmachine

Elke keer dat u een hypothesetest uitvoert, krijgt u een teststatistiek. Om te bepalen of de resultaten van de hypothesetest statistisch significant zijn, kunt u de teststatistiek vergelijken met een kritische Z-waarde . Als de absolute waarde van de teststatistiek groter is dan de kritische Z-waarde, zijn de testresultaten statistisch significant.

Om de kritische waarde Z op een TI-84-rekenmachine te vinden, kunt u de volgende functie gebruiken:

invNorm(waarschijnlijkheid, μ, σ)

Goud:

• waarschijnlijkheid: het significantieniveau
• μ: populatiegemiddelde
• σ: standaarddeviatie van de populatie

U kunt deze functie op een TI-84-rekenmachine openen door op 2nd en vervolgens op vars te drukken. Dit brengt u naar een DISTR- scherm waar u vervolgens invNorm() kunt gebruiken:

Deze tutorial deelt verschillende voorbeelden van het gebruik van de functie invNorm() om kritische Z-waarden op een TI-84-rekenmachine te vinden.

Voorbeeld 1: kritische waarde Z voor een test aan de linkerkant

Vraag: Vind de kritische Z-waarde voor een linkertoets met een significantieniveau van 0,05.

Antwoord: invNorm(.05, 0, 1) = -1,6449

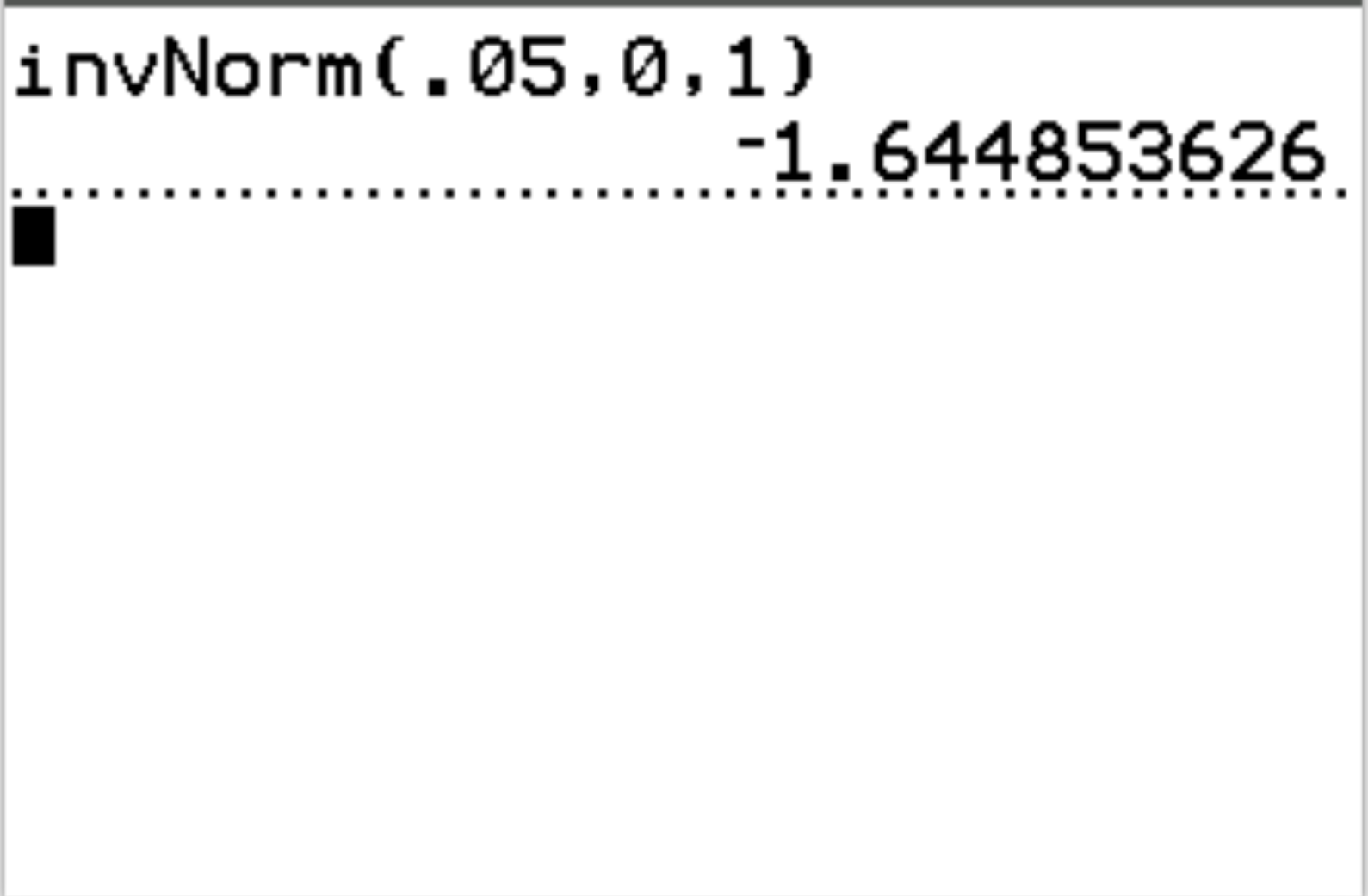
Interpretatie: Als de teststatistiek kleiner is dan -1,6449 , zijn de testresultaten statistisch significant bij α = 0,05.

Voorbeeld 2: Kritische Z-waarde voor een rechte staarttest

Vraag: Vind de kritische Z-waarde voor een rechterlaterale test met een significantieniveau van 0,10.

Antwoord: invT(1-.10, 0, 1) = 1,2816

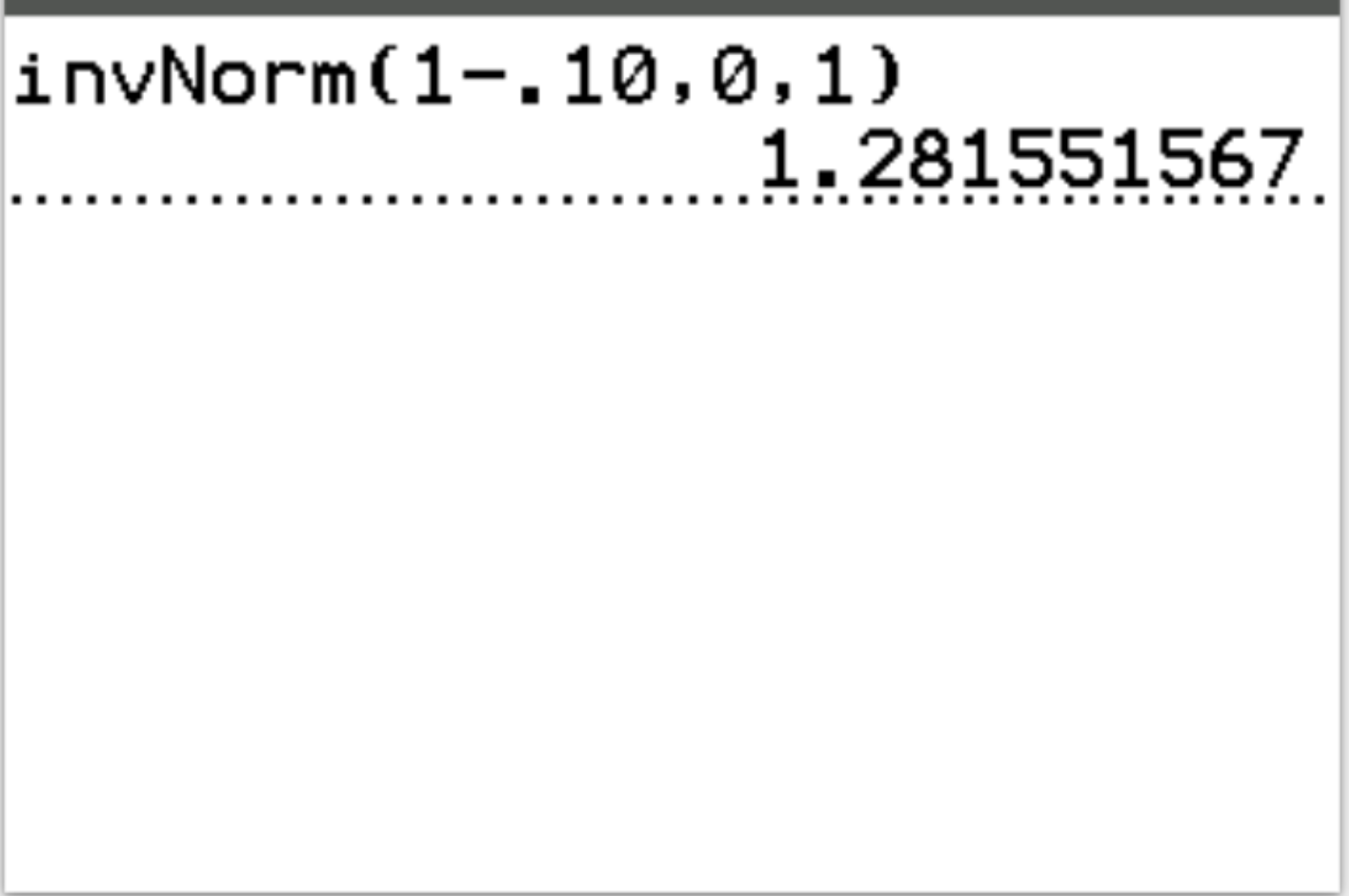
Interpretatie: Als de teststatistiek groter is dan 1,2816 , zijn de testresultaten statistisch significant bij α = 0,10.

Voorbeeld 3: kritische Z-waarde voor een tweezijdige test

Vraag: Vind de kritische Z-waarde voor een tweezijdige toets met een significantieniveau van 0,05.

Antwoord: invNorm(.05/2, 0, 1) = -1,96, 1,96

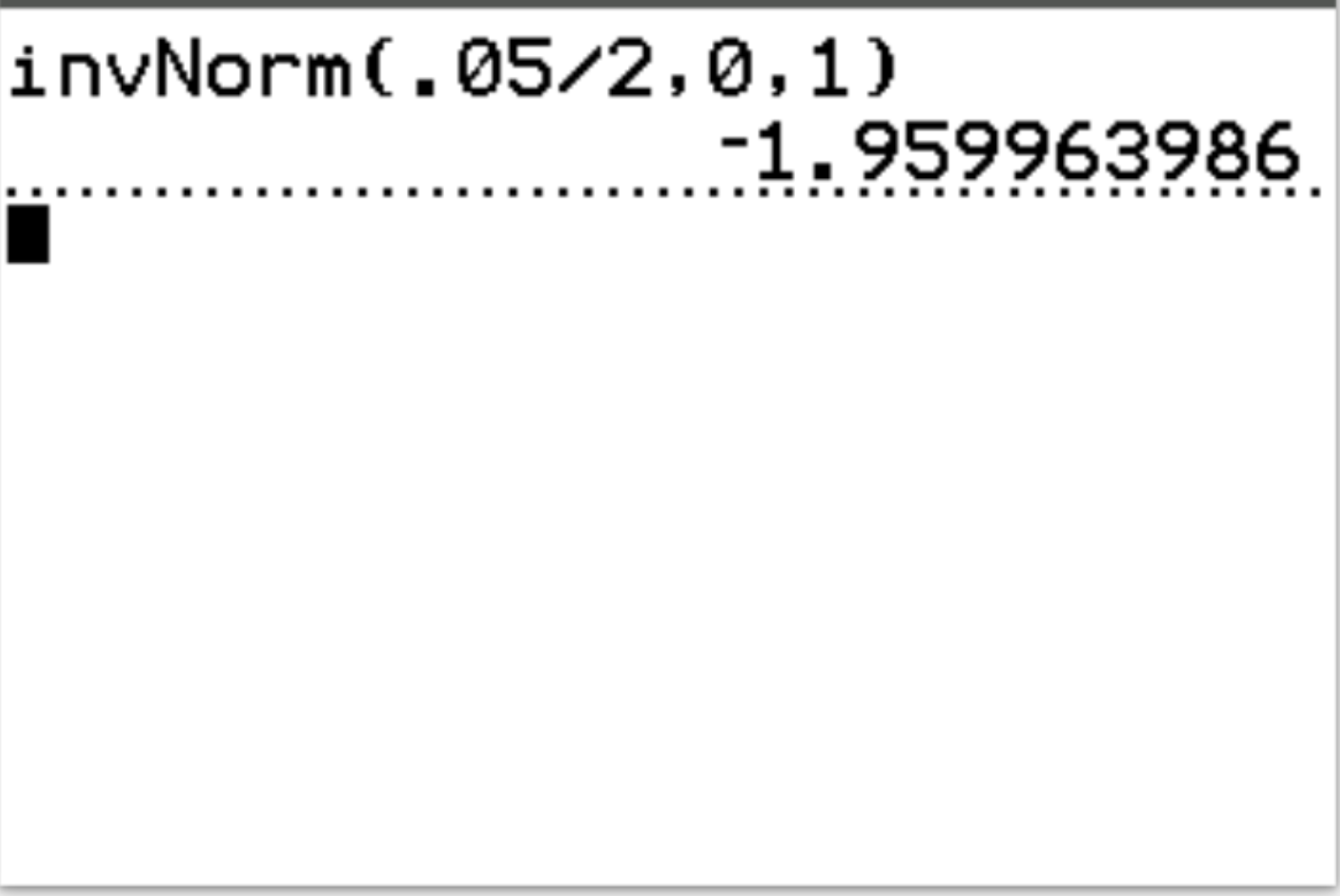
Interpretatie: Omdat dit een tweezijdige test is, hebben we eigenlijk twee kritische waarden: -1,96 en 1,96 . Als de teststatistiek kleiner is dan -1,96 of groter dan 1,96 , zijn de testresultaten statistisch significant bij α = 0,05.