Hoe z-scores in google spreadsheets te berekenen

In de statistiek vertelt een z-score ons hoeveel standaarddeviaties een waarde afwijkt van het gemiddelde . We gebruiken de volgende formule om een z-score te berekenen:

z = (X – μ) / σ

Goud:

• X is een enkele onbewerkte gegevenswaarde
• μ is het gemiddelde van de dataset
• σ is de standaardafwijking van de dataset

In deze tutorial wordt uitgelegd hoe u z-scores voor onbewerkte gegevenswaarden in Google Spreadsheets kunt berekenen.

Voorbeeld: z-scores in Google Spreadsheets

Stel dat we de volgende gegevensset hebben en de z-score voor elke ruwe gegevenswaarde willen vinden:

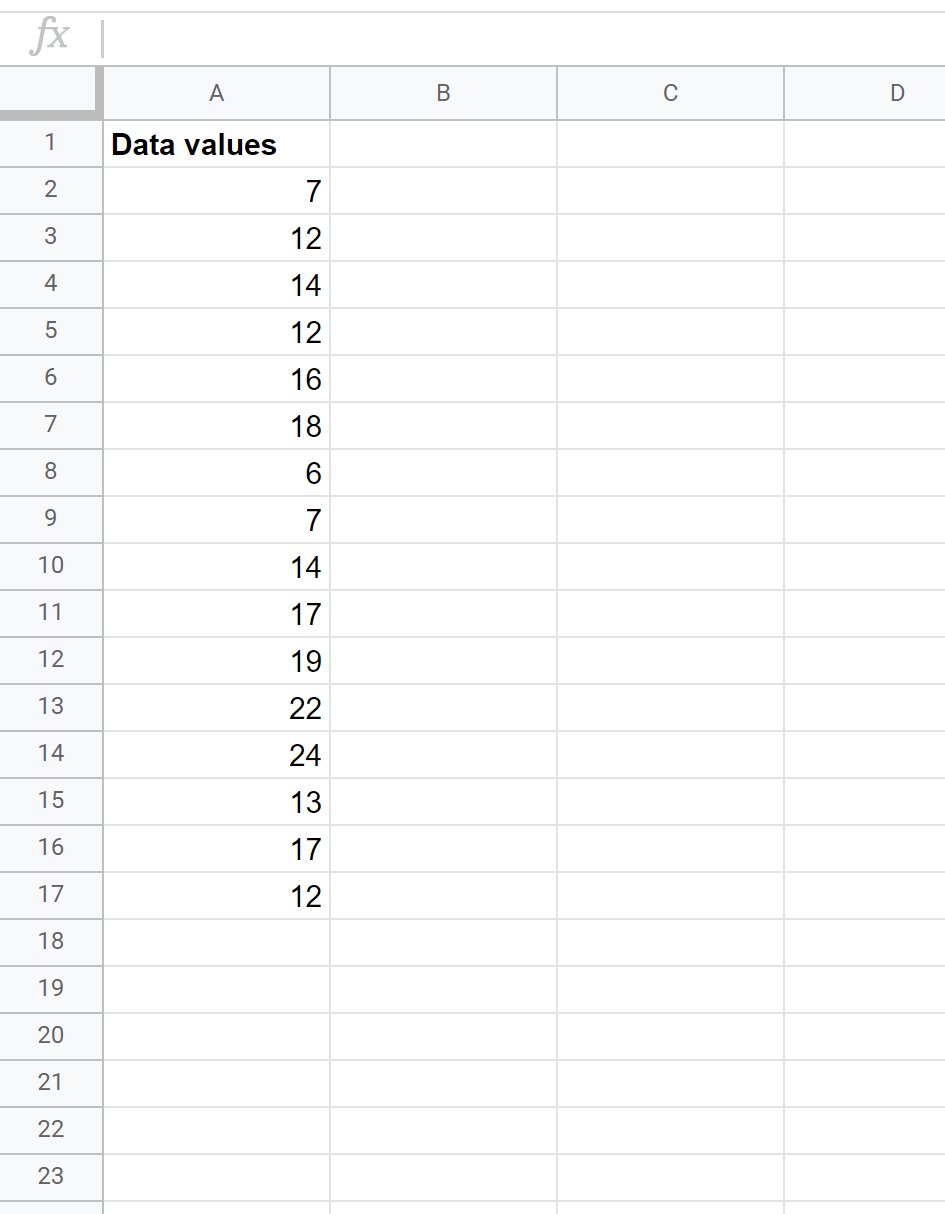
Hiervoor kunnen we de volgende stappen uitvoeren.

Stap 1: Zoek het gemiddelde en de standaardafwijking van de dataset.

Eerst moeten we het gemiddelde en de standaarddeviatie van de dataset vinden. De volgende formules laten zien hoe u dit doet:

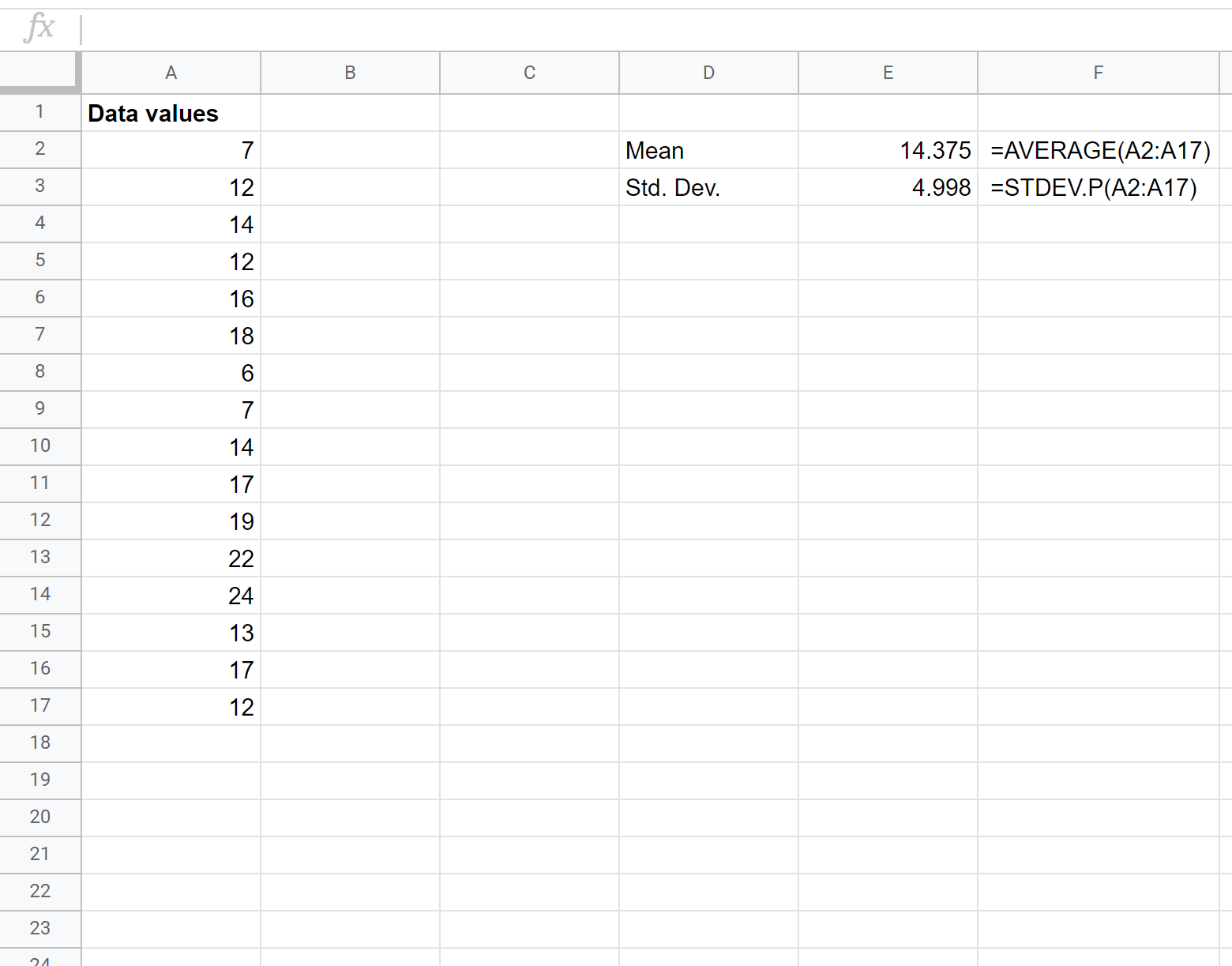
Het gemiddelde blijkt 14,375 te zijn en de standaarddeviatie is 4,998 .

Stap 2: Zoek de z-score voor de eerste ruwe gegevenswaarde.

Vervolgens vinden we de z-score voor de eerste ruwe gegevenswaarde door de volgende formule in cel B2 te typen:

= ( A2 – $E$2 ) / $E$3

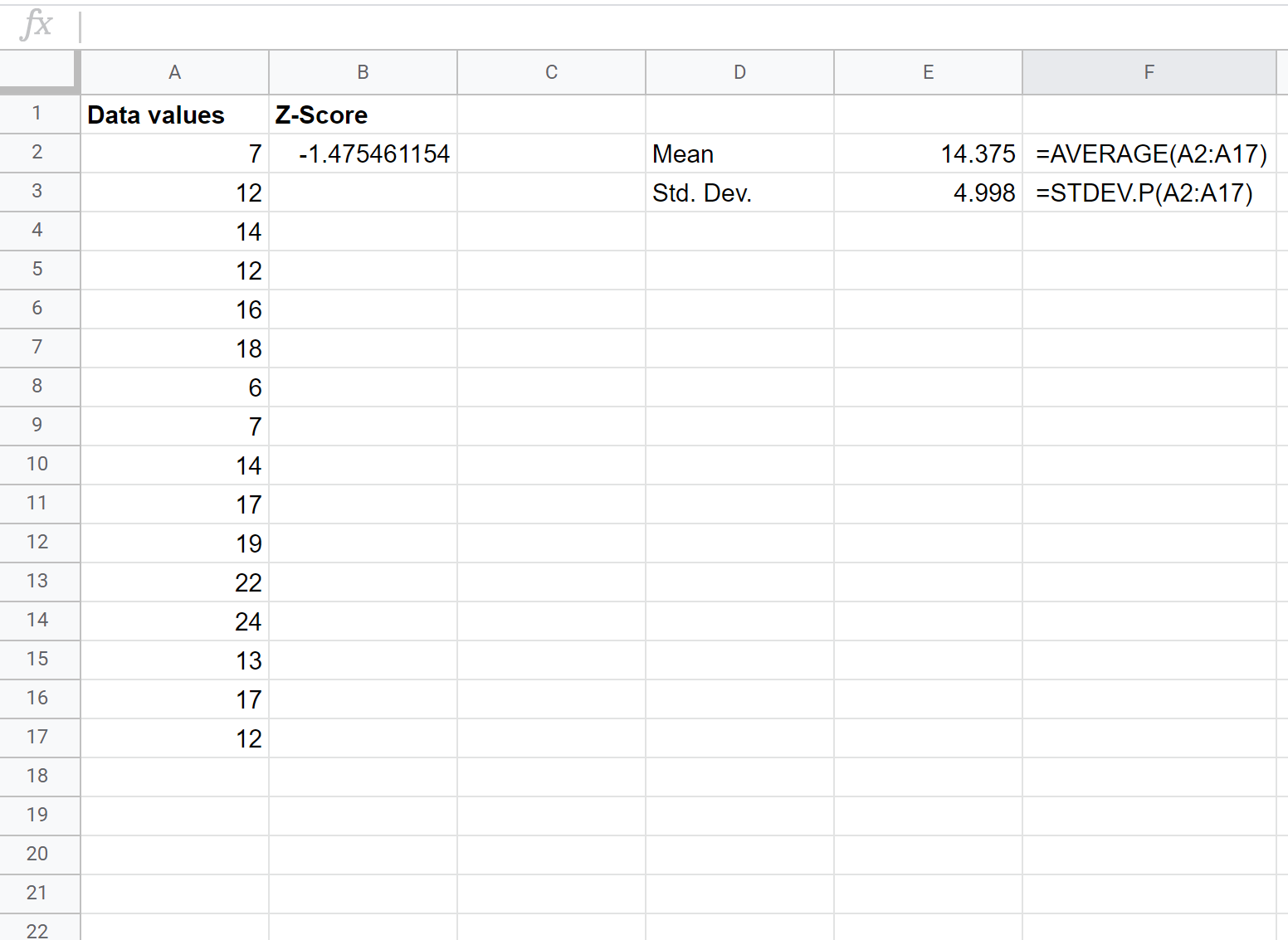
Stap 3: Zoek de z-scores voor alle resterende waarden.

Zodra we de eerste z-score hebben berekend, kunnen we de rest van kolom B markeren, te beginnen met cel B2 en op Ctrl+D drukken om de formule van cel B2 naar elk van de onderstaande cellen te kopiëren:

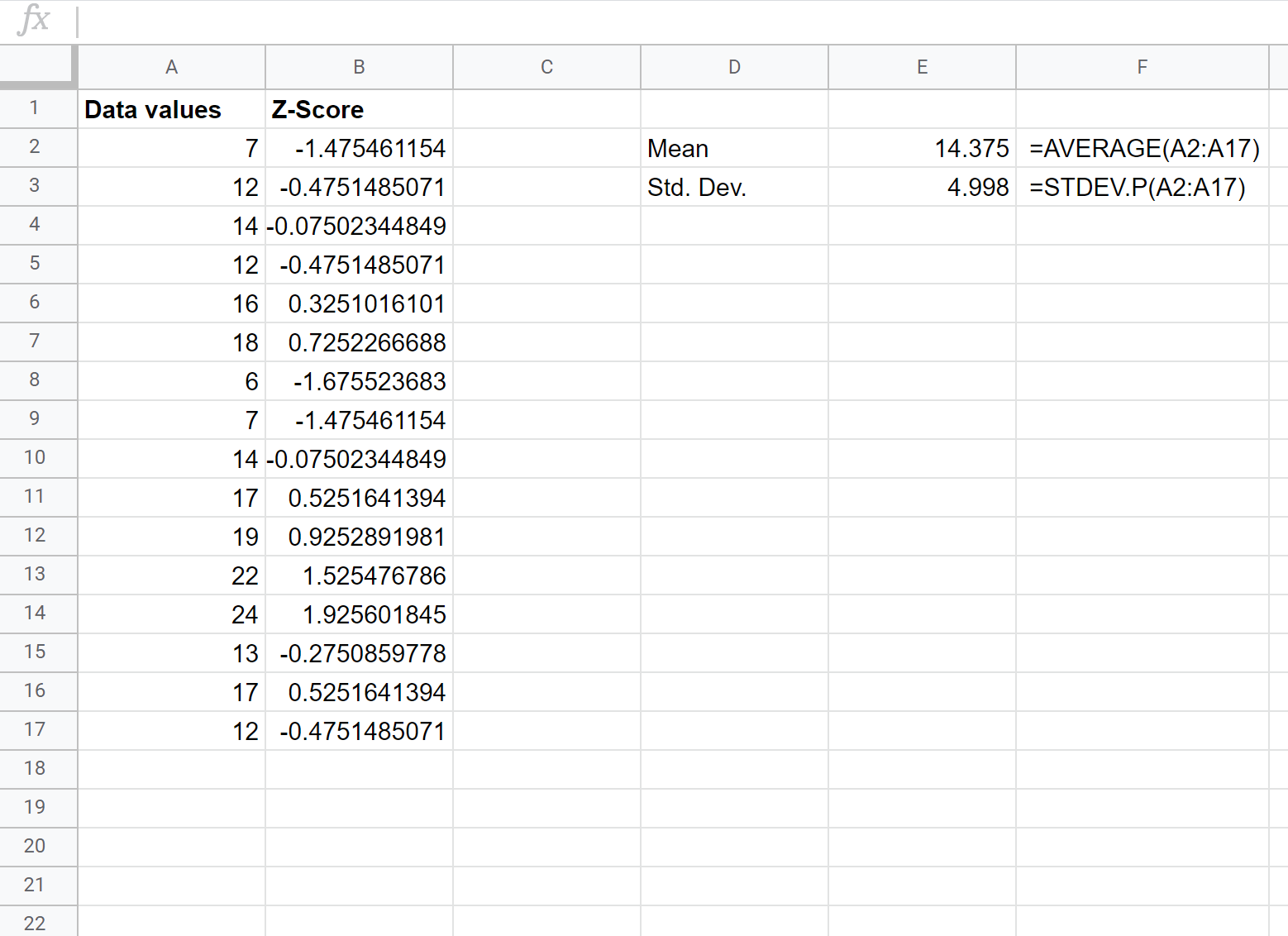
We hebben nu de z-score voor elke ruwe gegevenswaarde gevonden.

Hoe Z-scores te interpreteren

Een z-score vertelt ons eenvoudigweg hoeveel standaarddeviaties een waarde afwijkt van het gemiddelde.

In ons voorbeeld ontdekten we dat het gemiddelde 14,375 was en de standaarddeviatie 4,998 .

De eerste waarde in onze dataset was dus 7, die een z-score had van (7-14.375) / 4.998 = -1.47546 . Dit betekent dat de waarde “7” -1,47545 standaarddeviaties lager is dan het gemiddelde.

De volgende waarde in onze gegevens, 12, had een z-score van (12-14.375) / 4.998 = -0.47515 . Dit betekent dat de waarde „12“ -0,47515 standaardafwijkingen lager is dan het gemiddelde.

Hoe verder een waarde van het gemiddelde verwijderd is, hoe hoger de absolute waarde van de z-score voor die waarde zal zijn. De waarde 7 ligt bijvoorbeeld verder van het gemiddelde (14,375) dan de waarde 12, wat verklaart waarom 7 een z-score had met een grotere absolute waarde.

Aanvullende bronnen

Hoe Z-scores in Excel te berekenen
Hoe Z-scores in R te berekenen
Hoe Z-scores te berekenen op een TI-84-rekenmachine