Hoe z-scores in sas te berekenen

In de statistiek vertelt een z-score ons hoeveel standaarddeviaties een waarde afwijkt van het gemiddelde .

We gebruiken de volgende formule om een z-score te berekenen:

z = (X – μ) / σ

Goud:

• X is een enkele onbewerkte gegevenswaarde
• μ is het gemiddelde van de dataset
• σ is de standaardafwijking van de dataset

In het volgende voorbeeld ziet u hoe u z-scores voor onbewerkte gegevenswaarden in SAS berekent.

Voorbeeld: Bereken Z-scores in SAS

Stel dat we de volgende gegevensset in SAS maken:

 /*create dataset*/
data original_data;
    input values;
    datalines ;
7
12
14
12
16
18
6
7
14
17
19
22
24
13
17
12
;
run ;

/*view dataset*/
proc print data = original_data;

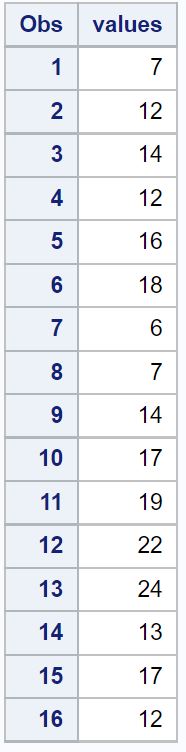
Stel nu dat we de z-score voor elke waarde in de dataset willen berekenen.

We kunnen proc sql gebruiken om dit te doen:

 /*create new variable that shows z-scores for each raw data value*/
proc sql ;
    select values, (values - mean(values)) / std(values) as z_scores
    from original_data;
quit ; 

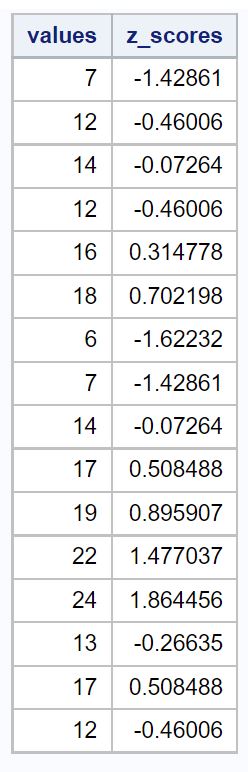
In de waardenkolom worden de oorspronkelijke gegevenswaarden weergegeven en in de z_scores- kolom wordt de z-score voor elke waarde weergegeven.

Hoe Z-scores in SAS te interpreteren

Een z-score vertelt ons hoeveel standaarddeviaties een waarde afwijkt van het gemiddelde.

Een z-score kan positief, negatief of nul zijn.

Een positieve z-score geeft aan dat een bepaalde waarde boven het gemiddelde ligt, een negatieve z-score geeft aan dat een bepaalde waarde onder het gemiddelde ligt, en een z-score van nul geeft aan dat een bepaalde waarde gelijk is aan het gemiddelde.

Als we het gemiddelde en de standaardafwijking van onze dataset zouden berekenen, zouden we ontdekken dat het gemiddelde 14,375 is en de standaardafwijking 5,162 .

De eerste waarde in onze dataset was dus 7, die een z-score had van (7-14.375) / 5.162 = -1.428 . Dit betekent dat de waarde “7” 1,428 standaarddeviaties lager is dan het gemiddelde.

De volgende waarde in onze gegevens, 12, had een z-score van (12-14.375) / 5.162 = -0.46 . Dit betekent dat de waarde “12” 0,46 standaardafwijkingen lager is dan het gemiddelde.

Hoe verder een waarde van het gemiddelde verwijderd is, hoe hoger de absolute waarde van de z-score voor die waarde zal zijn.

De waarde 7 ligt bijvoorbeeld verder van het gemiddelde (14,375) dan de waarde 12, wat verklaart waarom 7 een z-score had met een grotere absolute waarde.

Aanvullende bronnen

In de volgende artikelen wordt uitgelegd hoe u andere veelvoorkomende taken in SAS kunt uitvoeren:

Hoe uitschieters in SAS te identificeren
Hoe percentielen in SAS te berekenen
Hoe gemiddelde, mediaan en modus in SAS te berekenen