Hoe z-scores te berekenen op een ti-84-rekenmachine

Een z-score vertelt ons hoeveel standaarddeviaties een bepaalde waarde afwijkt van het gemiddelde. De z-score van een gegeven waarde wordt als volgt berekend:

z-score = (x – μ) / σ

Goud:

• x: individuele waarde
• μ: populatiegemiddelde
• σ: standaarddeviatie van de populatie

In deze tutorial wordt uitgelegd hoe u z-scores kunt berekenen op een TI-84-rekenmachine.

Hoe de Z-score van een enkele waarde te berekenen

Stel dat een verdeling normaal verdeeld is met een gemiddelde van 12 en een standaarddeviatie van 1,4 en we willen de z-score van een individuele waarde x = 14 berekenen. Om de z-score in een TI-84-rekenmachine te berekenen, zouden we eenvoudigweg typ de volgende formule:

Dit vertelt ons dat een individuele waarde van 14 een z-score van 1,4286 heeft. Met andere woorden: de waarde 14 ligt 1,4286 standaarddeviaties boven het gemiddelde.

Hoe de Z-score van meerdere waarden te berekenen

Stel dat we in plaats daarvan een lijst met gegevenswaarden hebben en dat we de z-score voor elke waarde in de lijst willen berekenen. In dit geval kunnen we de volgende stappen uitvoeren:

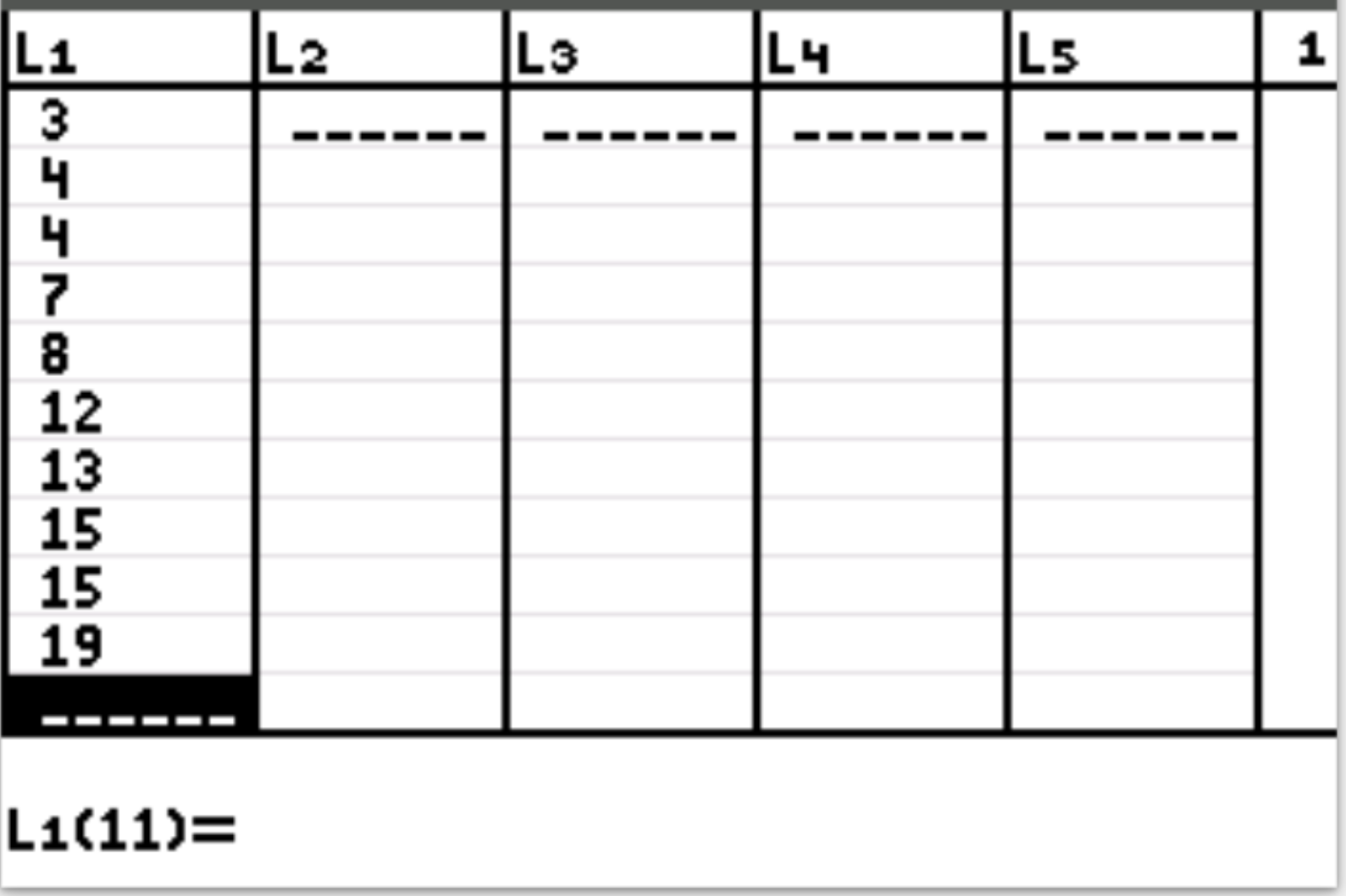
Stap 1: Voer de gegevens in.

Eerst zullen we de gegevenswaarden invoeren. Druk op Stat en vervolgens op BEWERKEN . Vul in kolom L1 de volgende waarden in:

Stap 2: Zoek het gemiddelde en de standaardafwijking van de gegevenswaarden.

Vervolgens zullen we het gemiddelde en de standaarddeviatie van de dataset vinden. Druk op Stat en scroll vervolgens naar CALC . Markeer Statistieken 1-Var en druk op Enter .

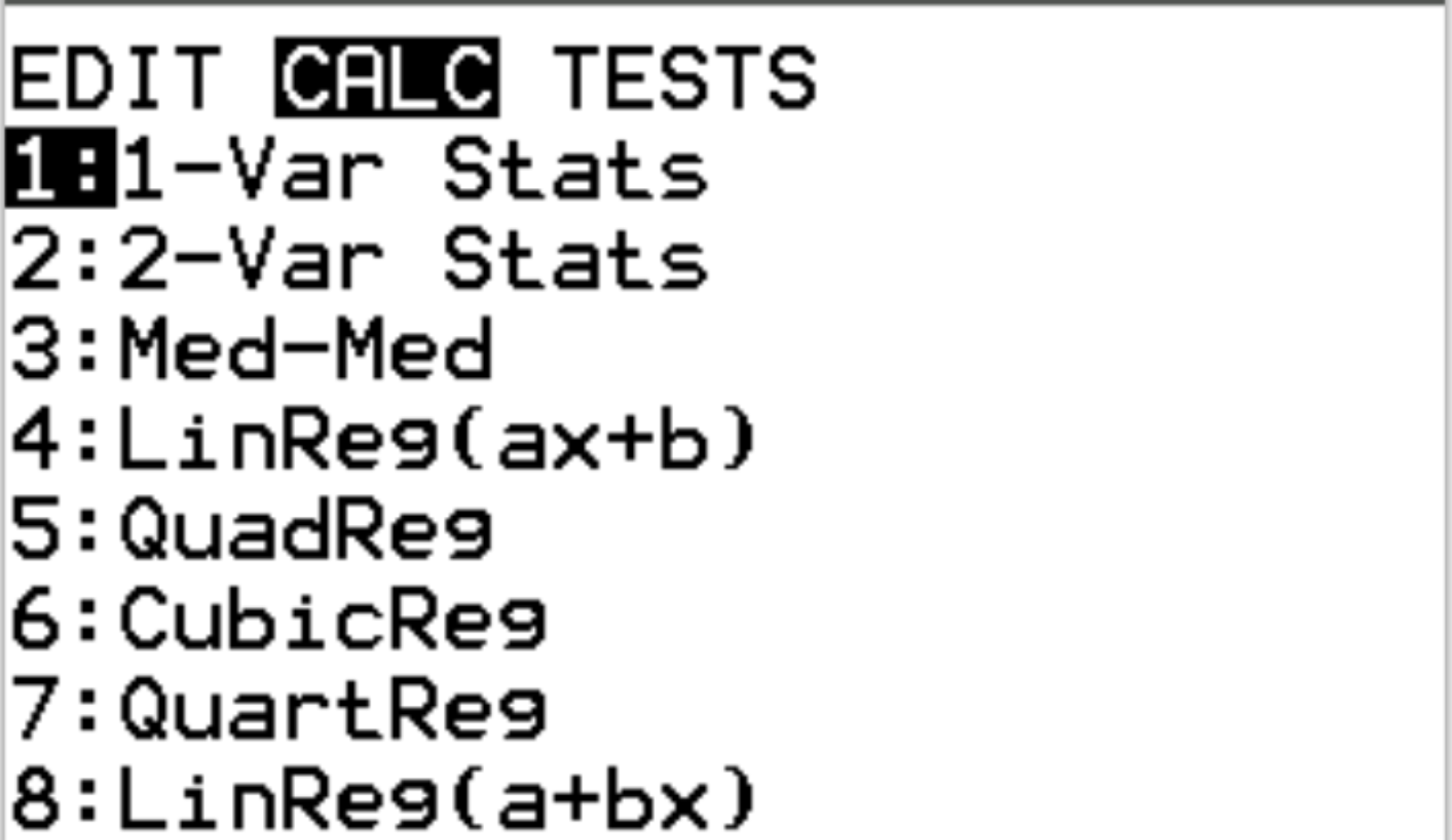
Zorg er voor Lijst voor dat L1 is gekozen, aangezien dit de kolom is waarin we onze gegevens hebben ingevoerd. Laat FreqList leeg. Markeer Bereken en druk op Enter .

De volgende uitvoer verschijnt:

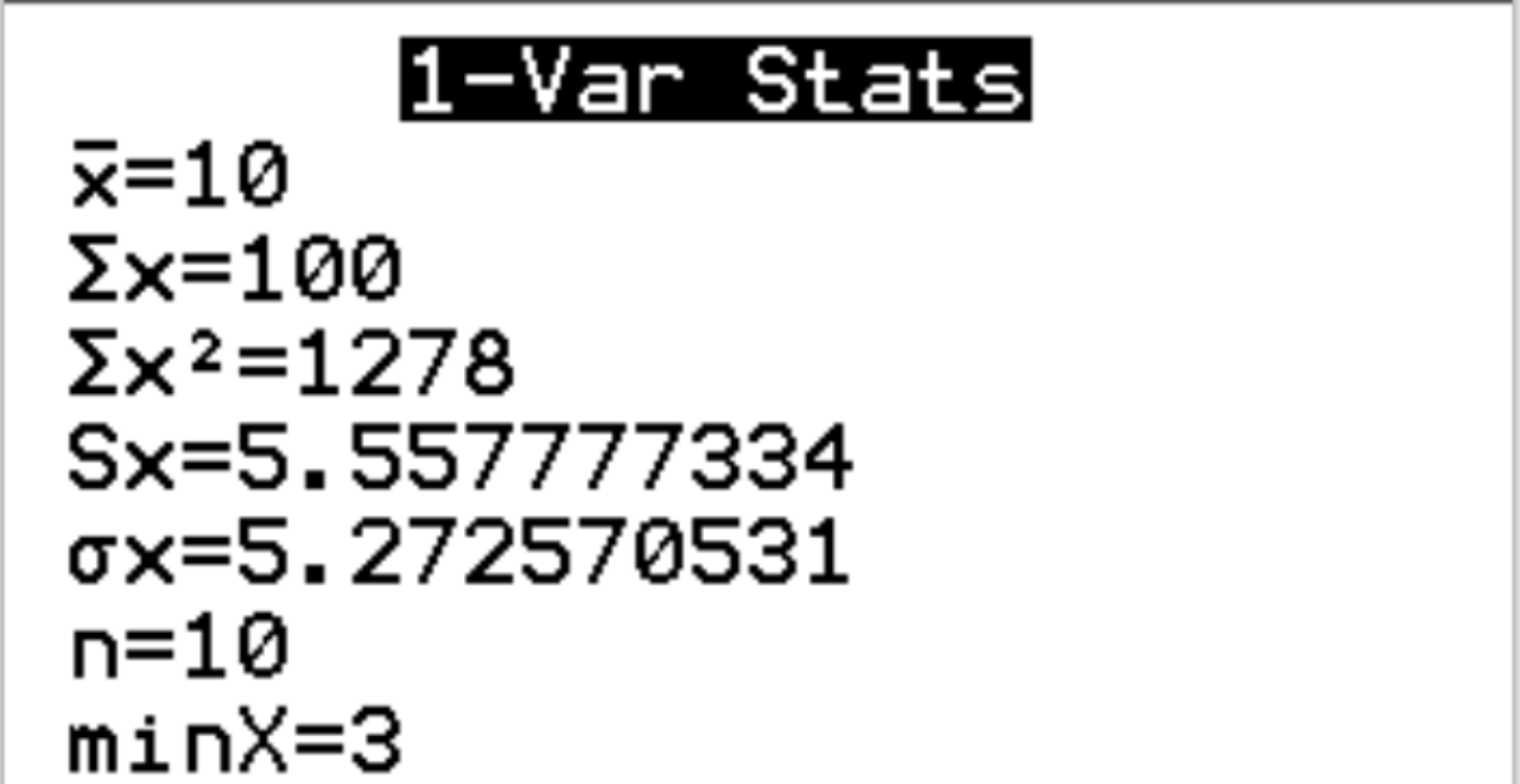
We kunnen zien dat het gemiddelde van de dataset x = 10 is en de standaardafwijking s _x = 5,558 . We zullen deze twee waarden in de volgende stap gebruiken om z-scores te berekenen.

Stap 3: Gebruik een formule om elke z-score te berekenen.

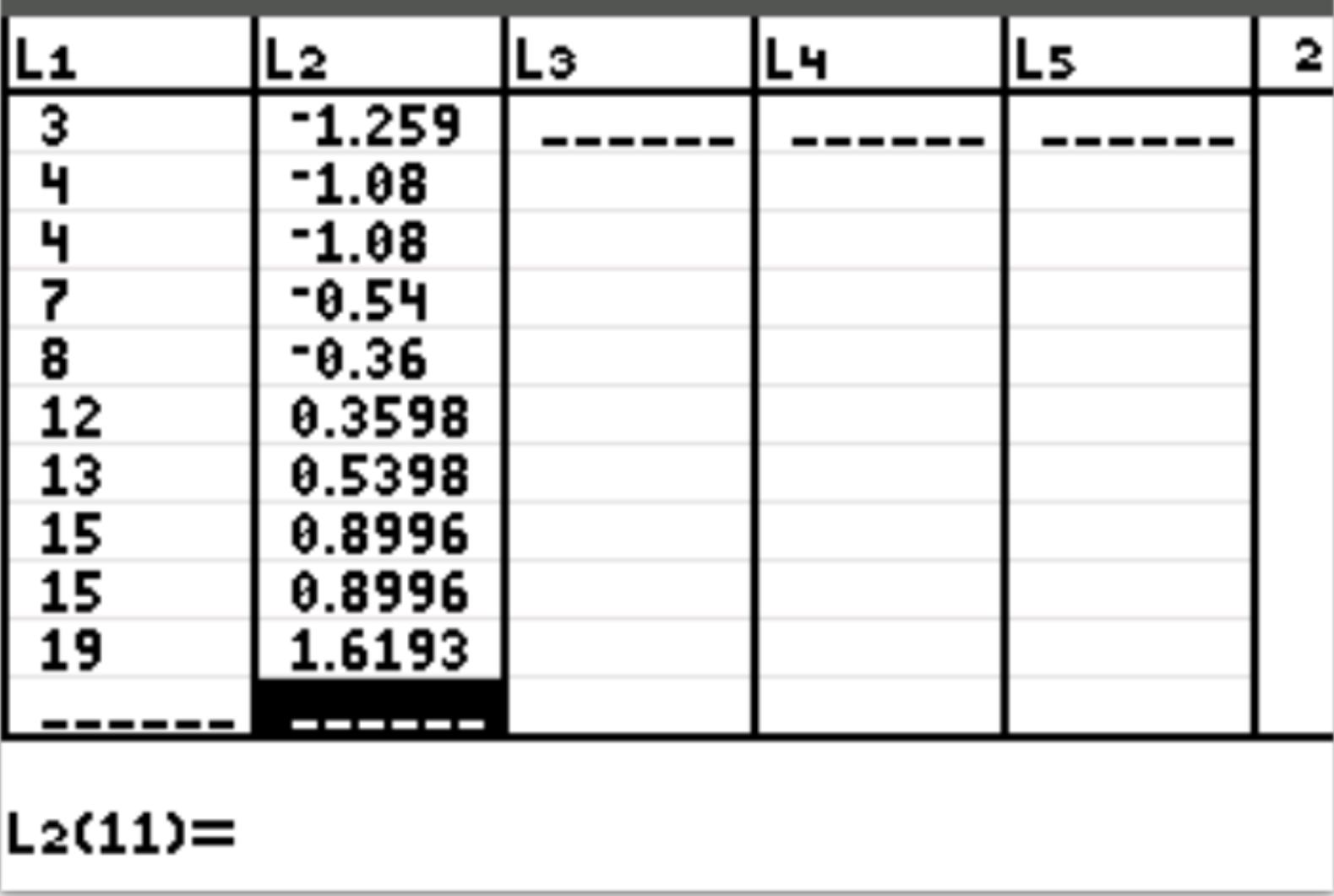
Vervolgens berekenen we de z-score voor elke individuele waarde in de dataset. Druk op Stat en vervolgens op BEWERKEN . Markeer L2 en typ de formule ( L1-10)/5.558 en druk vervolgens op Enter . De z-score van elke individuele waarde verschijnt automatisch in kolom L2:

Opmerking: Om “L1” in de formule in te voeren, drukt u op 2 en vervolgens op 1 .

Hoe Z-scores te interpreteren

Bedenk dat een z-score ons eenvoudigweg vertelt hoeveel standaarddeviaties een waarde van het gemiddelde afwijkt. Een z-score kan positief, negatief of gelijk aan nul zijn:

• Een positieve z-score geeft aan dat een bepaalde waarde boven het gemiddelde ligt.
• Een negatieve z-score geeft aan dat een bepaalde waarde onder het gemiddelde ligt.
• Een z-score van nul geeft aan dat een bepaalde waarde gelijk is aan het gemiddelde.

In ons voorbeeld ontdekten we dat het gemiddelde 10 was en de standaarddeviatie 5,558 .

De eerste waarde in onze dataset was dus 3, die een z-score had van (3-10)/5.558 = -1.259 . Dit betekent dat de waarde “3” 1,259 standaarddeviaties lager is dan het gemiddelde.

De volgende waarde in onze dataset, 4, had een z-score van (4-10) / 5,558 = -1,08 . Dit betekent dat de waarde “4” 1,08 standaarddeviaties lager is dan het gemiddelde.

Hoe verder een waarde van het gemiddelde verwijderd is, hoe hoger de absolute waarde van de z-score voor die waarde zal zijn.

De waarde 3 ligt bijvoorbeeld verder van het gemiddelde dan de waarde 4, wat verklaart waarom 3 een z-score had met een grotere absolute waarde.