Het verschil tussen z-waarden en p-waarden in statistieken

Twee termen die studenten vaak verwarren in de statistiek zijn z-waarden en p-waarden .

Om het verschil tussen deze termen te begrijpen, helpt het om z-tests te begrijpen.

Er zijn twee veelvoorkomende typen z-tests:

• Z-test met één steekproef : wordt gebruikt om te testen of een populatiegemiddelde gelijk is aan een bepaalde waarde.
• Z-test met twee steekproeven : wordt gebruikt om te testen of twee populatiegemiddelden gelijk zijn.

We gebruiken de volgende stappen om elke test uit te voeren:

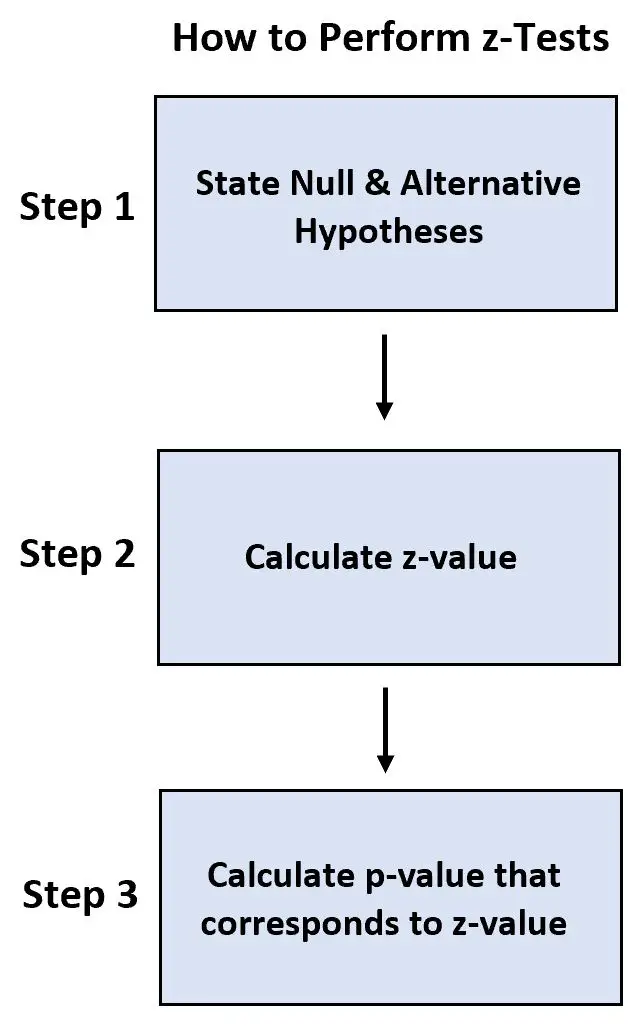
• Stap 1: Formuleer de nul- en alternatieve hypothese.
• Stap 2: Bereken de z-waarde.
• Stap 3: Bereken de p-waarde die overeenkomt met de z-waarde.

Voor elke test is de z-waarde een manier om het verschil tussen populatiegemiddelden te kwantificeren, en de p-waarde is de kans op het verkrijgen van een z-waarde met een absolute waarde die minstens zo groot is als we feitelijk in de steekproef hebben waargenomen. gegevens als de nulhypothese daadwerkelijk waar is.

Als de p-waarde kleiner is dan een bepaalde waarde (bijvoorbeeld 0,05), dan verwerpen we de nulhypothese van de test.

Voor elk type z-test zijn we geïnteresseerd in de p-waarde en gebruiken we de z-waarde eenvoudigweg als tussenstap om de p-waarde te berekenen.

Het volgende voorbeeld laat zien hoe u een z-waarde en de bijbehorende p-waarde voor een z-toets met twee steekproeven berekent en interpreteert.

Voorbeeld: Bereken en interpreteer Z-waarden en P-waarden

Neem aan dat de IQ-niveaus van individuen uit twee verschillende steden normaal verdeeld zijn, elk met een standaarddeviatie van de bevolking van 15.

Een wetenschapper wil weten of het gemiddelde IQ-niveau tussen individuen in stad A en stad B verschillend is. Ze selecteert daarom een eenvoudige willekeurige steekproef van twintig individuen uit elke stad en registreert hun IQ-niveaus:

Stad A : 82, 84, 85, 89, 91, 91, 92, 94, 99, 99, 105, 109, 109, 109, 110, 112, 112, 113, 114, 114

Stad B : 90, 91, 91, 91, 95, 95, 99, 99, 108, 109, 109, 114, 115, 116, 117, 117, 128, 129, 130, 133

U kunt als volgt een z-test met twee steekproeven uitvoeren met behulp van deze gegevens:

Stap 1: Formuleer de nul- en alternatieve hypothese.

Eerst zullen we de nul- en alternatieve hypothesen formuleren:

• H ₀ : μ ₁ = μ ₂ (de twee populatiegemiddelden zijn gelijk)
• H ₁ : μ ₁ ≠ μ ₂ (de twee populatiegemiddelden zijn niet gelijk)

Stap 2: Bereken de z-waarde.

Vervolgens zullen we een z-test met twee steekproeven uitvoeren in Excel met behulp van deze gegevens en vaststellen dat de z-waarde -1,71817 is.

Stap 3: Bereken de p-waarde.

We kunnen de Z-score naar P-waardecalculator gebruiken om te ontdekken dat de p-waarde die overeenkomt met de az-waarde van -1,71817 0,08577 is.

Omdat deze p-waarde niet kleiner is dan 0,05, hebben we niet voldoende bewijs om de nulhypothese te verwerpen.

We concluderen dus dat het gemiddelde IQ-niveau niet significant verschilt tussen de twee steden.

Merk op dat we eenvoudigweg de z-waarde als tussenstap hebben gebruikt om de p-waarde te berekenen.

De p-waarde is de werkelijke waarde waarin we geïnteresseerd waren, maar we moesten eerst de z-waarde berekenen.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u z-tests uitvoert met behulp van verschillende statistische software:

Hoe Z-tests uit te voeren in Excel
Hoe Z-tests uit te voeren in R
Hoe Z-tests uit te voeren in Python