Z-test met twee proporties: definitie, formule en voorbeeld

Een z-test met twee proporties wordt gebruikt om te testen op een verschil tussen twee populatieproporties.

In deze zelfstudie wordt het volgende uitgelegd:

• De motivatie voor het uitvoeren van een z-test met twee proporties.
• De formule voor het uitvoeren van een z-test met twee proporties.
• Een voorbeeld van hoe u een z-test met twee proporties uitvoert.

Z-test met twee proporties: motivatie

Stel dat we willen weten of er een verschil is tussen het aandeel inwoners dat een bepaalde wet in County A steunt, en het aandeel dat de wet in County B steunt.

Aangezien er in elke provincie duizenden inwoners zijn, zou het te tijdrovend en te duur zijn om elke individuele inwoner in elke provincie te onderzoeken.

In plaats daarvan zouden we een eenvoudige willekeurige steekproef van inwoners uit elke provincie kunnen nemen en het aandeel in het voordeel van de wet in elke steekproef kunnen gebruiken om het werkelijke verschil in verhoudingen tussen de twee provincies te schatten:

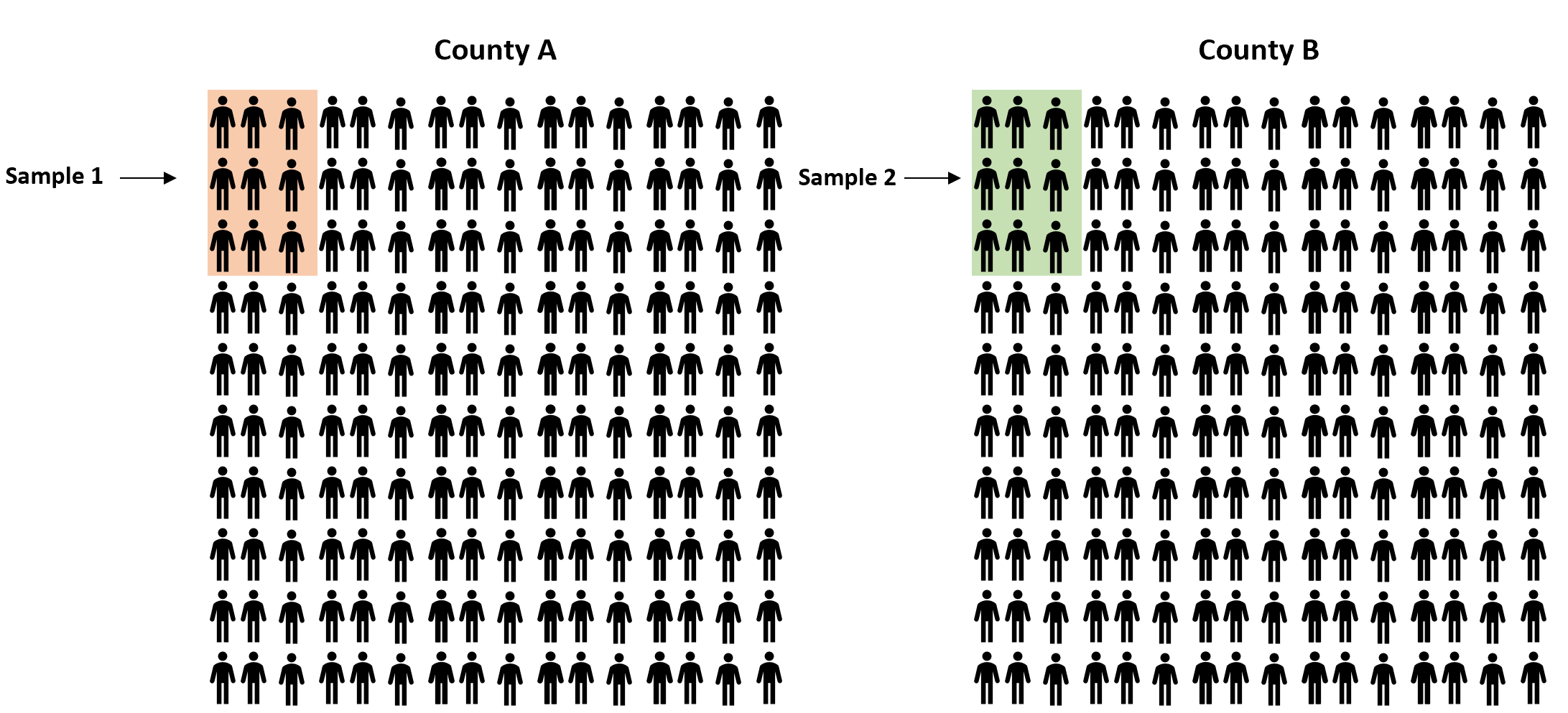
Het is echter vrijwel gegarandeerd dat het percentage inwoners dat vóór de wet is, tussen de twee steekproeven op zijn minst enigszins zal verschillen. De vraag is of dit verschil statistisch significant is . Gelukkig kunnen we deze vraag met een z-toets met twee proporties beantwoorden.

Z-test met twee proporties: formule

Een z-toets met twee proporties gebruikt altijd de volgende nulhypothese:

• H ₀ : μ ₁ = μ ₂ (de twee populatieverhoudingen zijn gelijk)

De alternatieve hypothese kan bilateraal, links of rechts zijn:

• H ₁ (tweezijdig): π ₁ ≠ π ₂ (de twee populatieverhoudingen zijn niet gelijk)
• H ₁ (links): π ₁ < π ₂ (het aandeel van bevolking 1 is kleiner dan het aandeel van bevolking 2)
• H ₁ (rechts): π ₁ > π ₂ (het aandeel van bevolking 1 is groter dan het aandeel van bevolking 2)

We gebruiken de volgende formule om de z-teststatistiek te berekenen:

z = (p ₁ -p ₂ ) / √ p(1-p)(1/n ₁ +1/n ₂ )

waarbij p ₁ en p ₂ de steekproefverhoudingen zijn, n ₁ en n ₂ de steekproefomvang zijn, en waarbij p het totale gepoolde aandeel is, als volgt berekend:

p = (p ₁ n ₁ + p ₂ n ₂ )/(n ₁ + n ₂ )

Als de p-waarde die overeenkomt met de z-teststatistiek kleiner is dan het gekozen significantieniveau (veel voorkomende keuzes zijn 0,10, 0,05 en 0,01), dan kun je de nulhypothese verwerpen.

Z-test met twee verhoudingen : voorbeeld

Stel dat we willen weten of er een verschil is tussen het aandeel inwoners dat een bepaalde wet in County A steunt, en het aandeel dat de wet in County B steunt.

Om dit te testen, zullen we een z-test met twee proporties uitvoeren op het significantieniveau α = 0,05 met behulp van de volgende stappen:

Stap 1: Verzamel voorbeeldgegevens.

Stel dat we een willekeurige steekproef van inwoners uit elke provincie verzamelen en de volgende informatie verkrijgen:

Voorbeeld 1:

• Steekproefomvang n ₁ = 50
• Aandeel ten gunste van de wet p ₁ = 0,67

Voorbeeld 2:

• Steekproefomvang n ₂ = 50
• Aandeel ten gunste van de wet p ₂ = 0,57

Stap 2: Definieer aannames.

We zullen de z-test met twee proporties uitvoeren met de volgende hypothesen:

• H ₀ : π ₁ = π ₂ (de twee populatieverhoudingen zijn gelijk)
• H ₁ : π ₁ ≠ π ₂ (de twee populatieverhoudingen zijn niet gelijk)

Stap 3: Bereken de z- teststatistiek.

Eerst berekenen we het totale gepoolde aandeel:

p = (p ₁ n ₁ + p ₂ n ₂ )/(n ₁ +n ₂ ) = (0,67(50) + 0,57(50))/(50+50) = 0,62

Vervolgens zullen we de z- teststatistiek berekenen:

z = (p ₁ -p ₂ ) / √ p(1-p)(1/n ₁ +1/n ₂ ) = (.67-.57) / √ .62(1-.62)(1/50 + 1/50 ) = 1,03

Stap 4: Bereken de p-waarde van de z- teststatistiek.

Volgens de P-waarde Z-score-calculator is de tweezijdige p-waarde geassocieerd met z = 1,03 0,30301 .

Stap 5: Trek een conclusie.

Omdat deze p-waarde niet lager is dan ons significantieniveau α = 0,05, slagen we er niet in de nulhypothese te verwerpen. We hebben niet voldoende bewijs om te zeggen dat het aandeel inwoners dat vóór deze wet is, tussen de twee provincies verschillend is.

Opmerking: u kunt deze volledige Z-test met twee proporties ook uitvoeren door eenvoudigweg de Z-testcalculator met twee proporties te gebruiken.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u een z-test met twee proporties uitvoert met behulp van verschillende statistische software:

Hoe u een Z-test met twee proporties uitvoert in Excel
Hoe u een Z-test met twee proporties uitvoert in SAS
Z-testcalculator met twee proporties