Hoe u de lineaire regressievergelijking uit een tabel kunt vinden

Vaak wilt u misschien een lineaire regressievergelijking uit een tabel met gegevens vinden.

Stel dat u bijvoorbeeld de volgende gegevenstabel ontvangt:

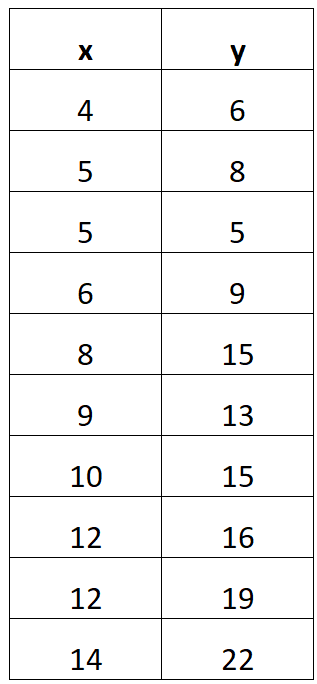
Het volgende stapsgewijze voorbeeld laat zien hoe u een lineaire regressievergelijking uit deze gegevenstabel kunt vinden.

Stap 1: Bereken X*Y, X ² en Y ²

Eerst berekenen we de volgende statistieken voor elke rij:

• x*y
• ^x2
• en ²

De volgende schermafbeelding laat zien hoe u dit doet:

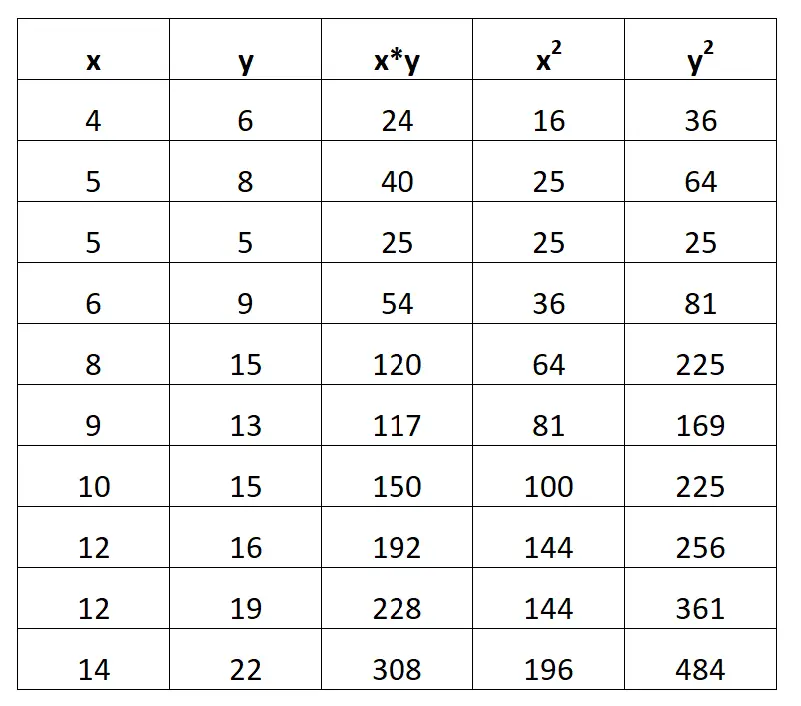
Stap 2: Bereken ΣX, ΣY, ΣX*Y, ΣX ² en ΣY ²

Vervolgens berekenen we de som van elke kolom:

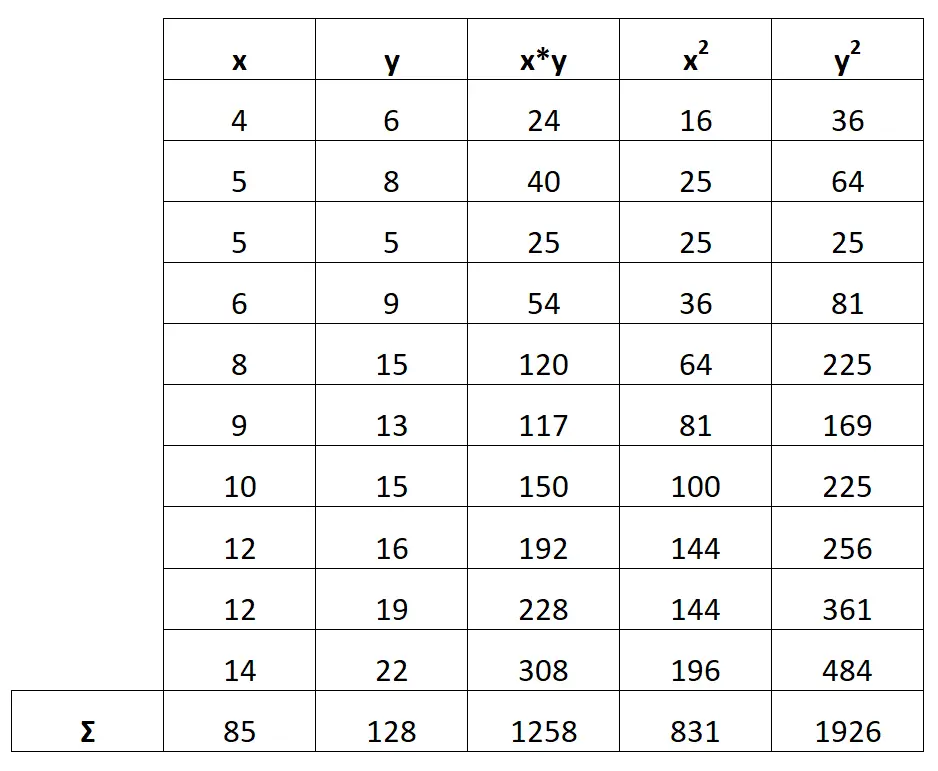
Stap 3: Bereken b ₀

De formule voor het berekenen van het snijpunt van de regressievergelijking, b ₀ , is:

• b ₀ = ((Σy)(Σx ² ) – (Σx)(Σxy)) / (n(Σx ² ) – (Σx) ² )
• _b0 = ((128)(831) – (85)(1258)) / (10(831) – (85) ² )
• _b0 = -0,518

Opmerking : In de formule vertegenwoordigt n het totale aantal waarnemingen. In dit voorbeeld waren er in totaal 10 waarnemingen.

Stap 4: Bereken b ₁

De formule voor het berekenen van de helling van de regressievergelijking, b ₁ , is:

• b ₁ = (n(Σxy) – (Σx)(Σy)) / (n(Σx ² ) – (Σx) ² )
• _b1 = (10(1258) – (85)(128)) / (10(831) – (85) ² )
• _b1 = 1,5668

Stap 5: Schrijf de lineaire regressievergelijking

De uiteindelijke lineaire regressievergelijking kan worden geschreven als:

• ŷ = _b0 + _b1 x

Onze lineaire regressievergelijking zou dus als volgt worden geschreven:

• ŷ = -0,518 + 1,5668x

We kunnen verifiëren dat dit antwoord juist is door de waarden uit de tabel in de eenvoudige lineaire regressiecalculator in te voeren:

We kunnen zien dat de lineaire regressievergelijking van de rekenmachine overeenkomt met de vergelijking die we handmatig hebben berekend.

Aanvullende bronnen

De volgende zelfstudies bieden aanvullende informatie over lineaire regressie:

Inleiding tot eenvoudige lineaire regressie
Inleiding tot meervoudige lineaire regressie
Hoe regressiecoëfficiënten te interpreteren