Hoe u de omvang van een boxplot kunt vinden: met voorbeelden

Een boxplot is een type plot dat de vijfcijferige samenvatting van een dataset weergeeft, waaronder:

• De minimumwaarde
• Het eerste kwartiel (het 25e percentiel)
• De gemiddelde waarde
• Het derde kwartiel (het 75e percentiel)
• De maximale waarde

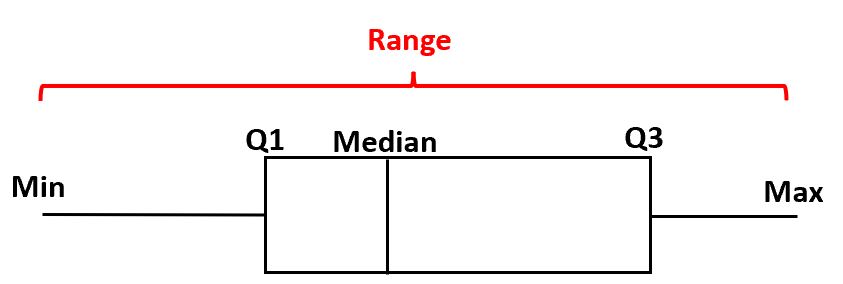
Om een boxplot te maken, tekenen we een box van het eerste tot en met het derde kwartiel. Vervolgens tekenen we een verticale lijn op de mediaan. Ten slotte tekenen we ‘snorharen’ van de kwartielen tot aan de minimale en maximale waarde.

Het bereik van een boxplot is het verschil tussen de maximale waarde en de minimale waarde.

• Bereik = Maximaal – Minimaal

Om de omvang van een gegeven boxplot te vinden, kunnen we eenvoudigweg de waarde aan de onderste snorhaar aftrekken van de waarde aan de bovenste snorhaar.

De volgende voorbeelden laten zien hoe u in de praktijk de omvang van een boxplot kunt vinden.

Voorbeeld 1: Examenresultaten

De volgende boxplot toont de verdeling van de scores op een bepaald universitair examen. Wat is het bereik van examenresultaten?

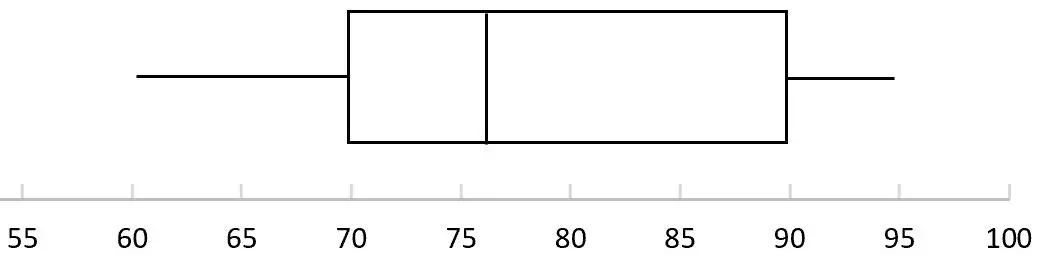
Om deze vraag te beantwoorden, kunnen we de volgende waarden op de boxplot vinden:

• Bereik = Maximaal – Minimaal
• Bereik = 95 – 60
• Bereik = 35

Het bereik van examenresultaten is 35 .

Voorbeeld 2: Gescoorde punten

De volgende boxplot toont de verdeling van de punten die zijn gescoord door basketbalspelers in een bepaalde competitie. Hoe wijdverspreid is de verspreiding?

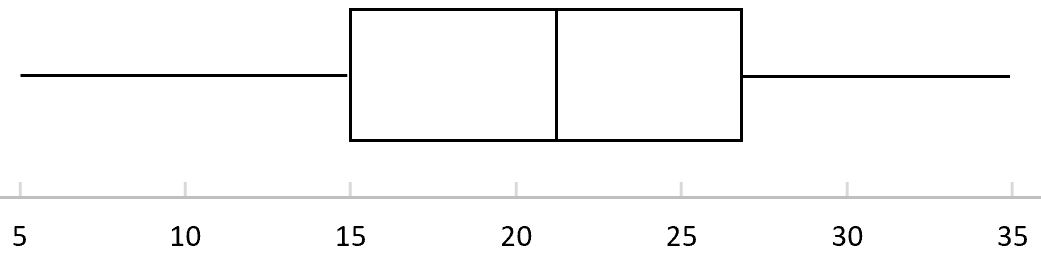
Om deze vraag te beantwoorden, kunnen we de volgende waarden op de boxplot vinden:

• Bereik = Maximaal – Minimaal
• Bereik = 35 – 5
• Bereik = 30

De omvang van de verdeling is 30 .

Voorbeeld 3: Vergelijking van planthoogtes

De volgende boxplots tonen de hoogteverdeling voor twee verschillende plantensoorten: rood en blauw. Welke distributie heeft een groter bereik?

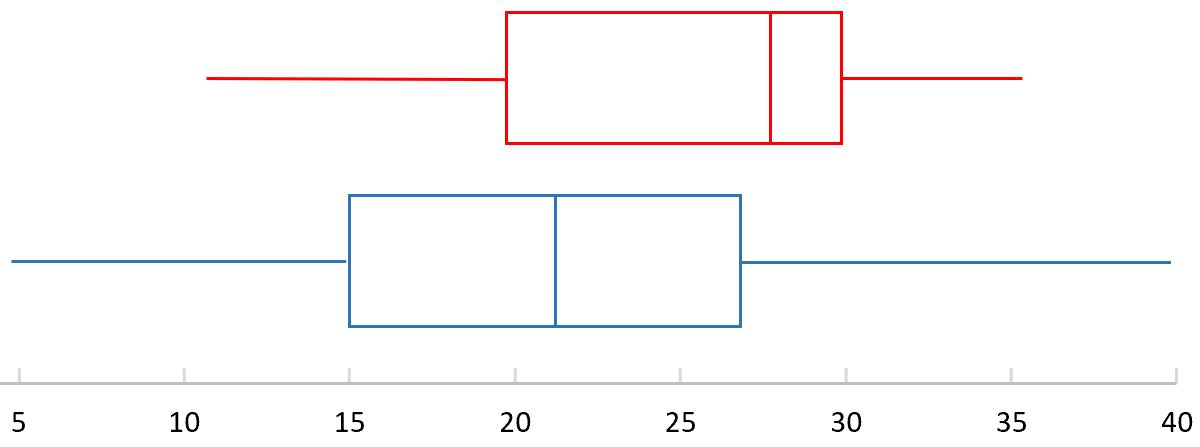
Laten we eerst de omvang van het rode vak bepalen:

• Bereik = Maximaal – Minimaal
• Bereik = 35 – 10
• Bereik = 25

Laten we vervolgens de omvang van de blue box-plot bepalen:

• Bereik = Maximaal – Minimaal
• Bereik = 40 – 5
• Bereik = 35

Het verspreidingsgebied van de blauwe soort is groter.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over boxplots:

Boxplotgenerator
Boxplots vergelijken
Hoe asymmetrie in boxplots te identificeren
Hoe het interkwartielbereik van een boxplot te vinden