Średnia harmoniczna

Przez Benjamin Anderson 6 sierpnia, 2023 Statystyka 0 komentarzy

Tutaj wyjaśniamy, czym jest średnia harmoniczna i jak jest obliczana (wzór). Dodatkowo krok po kroku obliczamy średnią harmoniczną przykładu. Znajdziesz tu także kalkulator pozwalający obliczyć średnią harmoniczną dowolnego zbioru danych. I wreszcie będziesz mógł zobaczyć, jakie są właściwości średniej harmonicznej.

Co to jest średnia harmoniczna?

Średnia harmoniczna jest centralną miarą pozycji statystyki opisowej. Średnią harmoniczną oblicza się, dzieląc całkowitą liczbę danych statystycznych przez sumę odwrotności każdej wartości.

Średnia harmoniczna służy do obliczania średnich prędkości, czasów lub wykonywania obliczeń elektronicznych. Cecha ta odróżnia średnią harmoniczną od innych typów średnich, często stosowanych przy obliczaniu średnich cen lub wartości procentowych.

Zatem wzór na średnią harmoniczną jest następujący:

Średnia harmoniczna jest zwykle oznaczana przez duże H.

Inne istniejące typy średnich to średnia arytmetyczna, średnia ważona, średnia kwadratowa i średnia geometryczna. Średnia harmoniczna ma zalety i wady w porównaniu do innych typów średnich, poniżej zobaczymy, jakie one są.

Jak obliczyć średnią harmoniczną

Aby obliczyć średnią harmoniczną, należy wykonać następujące kroki:

Oblicz odwrotność poszczególnych danych statystycznych w próbie.
Dodaj wszystkie obliczone odwrotności.
Podziel całkowitą liczbę danych przez sumę z poprzedniego kroku.
Otrzymany wynik jest średnią harmoniczną próby statystycznej.

👉 Jak widać, wzięcie średniej harmonicznej zbioru danych wymaga wielu operacji, dlatego robienie tego ręcznie jest dość pracochłonne. Dlatego do obliczenia średniej harmonicznej zalecamy skorzystanie z poniższego kalkulatora.

Przykład średniej harmonicznej

Po zapoznaniu się z teorią średniej harmonicznej dowiemy się, jak znaleźć średnią harmoniczną zbioru danych, rozwiązując krok po kroku przykład ceny akcji.

Osoba kupuje akcje spółki co roku przez 5 kolejnych lat. W tym okresie cena akcji podlegała dużym wahaniom: w pierwszym roku każda akcja była warta 7 euro, w drugim roku 10 euro, w trzecim roku 15 euro, w czwartym roku spółka poniosła znaczne straty finansowe, a spółka cena spadła do 6 euro za akcję i ostatecznie w piątym roku firma dokonała dużej inwestycji, która podniosła cenę do 11 euro. Jaka była średnia cena nabycia akcji?

Jedną z opcji byłoby obliczenie średniej arytmetycznej, czyli zsumowanie wszystkich cen i podzielenie ich przez pięć. Ponieważ jednak zakupów dokonywano w różnych latach, przyjmowanie średniej arytmetycznej byłoby błędem. Musimy zatem znaleźć średnią harmoniczną wszystkich cen.

Następnie stosujemy wzór na średnią harmoniczną:

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}+\frac{1}{x_4}+\frac{1}{x_5}}$

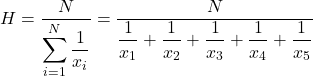
Następnie podstawiamy problematyczne wartości cen do wzoru i obliczamy średnią harmoniczną:

$\displaystyle H=\frac{5}{\displaystyle\frac{1}{7}+\frac{1}{10}+\frac{1}{15}+\frac{1}{6}+\frac{1}{11}}=8,82$

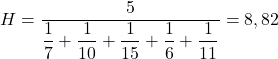
Musisz wstawić pięć do licznika ułamka, ponieważ istnieje pięć różnych informacji.

Zatem średnia cena akcji zakupionych w tym okresie wynosi 8,82 euro za akcję.

Kalkulator średniej harmonicznej

Za pomocą poniższego kalkulatora możesz obliczyć średnią harmoniczną dowolnego zestawu danych statystycznych.

Liczby należy wprowadzać, stosując kropkę jako separator dziesiętny i oddzielając je spacją. Pamiętaj, że aby znaleźć średnią harmoniczną, żadna wartość nie może wynosić zero.

Własności średniej harmonicznej

Średnia harmoniczna ma następujące cechy:

Duże wartości mają niewielki wpływ na średnią harmoniczną zespołu, to znaczy bardzo duża wartość w stosunku do innych danych nie spowoduje zauważalnej zmiany średniej harmonicznej.

Z drugiej strony mała wartość znacząco wpływa na średnią harmoniczną zespołu, znacznie zmniejszając jej wartość. Rzeczywiście, odwrotność mianownika wzoru przyjmuje wtedy bardzo duże wartości.

Średniej harmonicznej nie można obliczyć, jeśli którakolwiek z danych wynosi zero, ponieważ spowodowałoby to nieokreśloność wzoru. Mówi się wówczas, że średnia harmoniczna jest nieokreślona.

Odwrotność średniej harmonicznej jest równa średniej arytmetycznej odwrotności obserwacji.

Dla tej samej grupy danych średnia harmoniczna będzie mniejsza lub równa średniej arytmetycznej.

$\cfrac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}\leq \cfrac{x_1+x_2+\dots+x_N}{N}$

Oblicz średnią harmoniczną w programie Excel

Jak widzieliśmy, ręczne obliczanie średniej harmonicznej może być dość uciążliwe, ponieważ należy wykonać wiele obliczeń. A sytuacja staje się jeszcze bardziej skomplikowana, gdy masz dużą ilość danych. Dlatego do obliczenia średniej harmonicznej zalecamy skorzystanie z kalkulatora lub programu Excel.

Średnią harmoniczną w programie Excel oblicza się ze wzoru MEAN.ARMO . Oznacza to, że aby obliczyć średnią harmoniczną zbioru danych, należy je skopiować do arkusza Excel i wprowadzić wszystkie dane do funkcji MEAN.ARMO .

Na przykład, aby uzyskać średnią harmoniczną z ćwiczenia, które rozwiązaliśmy powyżej, wpisz w komórce Excela =MEDIA.ARMO(7;10;15;6;11) .

Należy pamiętać, że jeśli którakolwiek z wartości będzie równa zero, funkcja zwróci błąd, ponieważ nie można wyznaczyć średniej harmonicznej zbioru wartości statystycznych, jeśli którakolwiek z nich wynosi zero.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej