Jak wykonać test tukeya w r

Jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica pomiędzy średnimi z trzech lub więcej niezależnych grup.

Jeśli ogólna wartość p tabeli ANOVA jest poniżej pewnego poziomu istotności, wówczas mamy wystarczające dowody, aby stwierdzić, że co najmniej jedna ze średnich grupowych różni się od pozostałych.

Nie mówi nam to jednak , które grupy różnią się od siebie. To po prostu mówi nam, że nie wszystkie średnie grupowe są równe. Aby dokładnie wiedzieć, które grupy się od siebie różnią, należy przeprowadzićtest post hoc .

Jednym z najczęściej stosowanych testów post hoc jest test Tukeya , który umożliwia przeprowadzenie porównań parami pomiędzy średnimi każdej grupy, kontrolując jednocześnie współczynnik błędu rodzinnego .

W tym samouczku wyjaśniono, jak wykonać test Tukeya w języku R.

Uwaga: Jeśli którakolwiek z grup w Twoim badaniu jest uważana za grupę kontrolną, powinieneś zamiast tego zastosować test Dunnetta jako test post-hoc.

Przykład: test Tukeya w R

Krok 1: Dopasuj model ANOVA.

Poniższy kod pokazuje, jak utworzyć fałszywy zbiór danych z trzema grupami (A, B i C) i dopasować do danych jednokierunkowy model ANOVA, aby określić, czy średnie wartości każdej grupy są równe:

 #make this example reproducible
set.seed(0)

#create data
data <- data.frame(group = rep (c("A", "B", "C"), each = 30),
                   values = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#view first six rows of data
head(data)

  group values
1 A 2.6900916
2 A 0.7965260
3 A 1.1163717
4 A 1.7185601
5 A 2.7246234
6 A 0.6050458

#fit one-way ANOVA model
model <- aov (values~group, data=data)

#view the model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)    
group 2 98.93 49.46 30.83 7.55e-11 ***
Residuals 87 139.57 1.60                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Widzimy, że ogólna wartość p z tabeli ANOVA wynosi 7,55e-11 . Ponieważ liczba ta jest mniejsza niż 0,05, mamy wystarczające dowody, aby stwierdzić, że średnie wartości w każdej grupie nie są równe. Możemy więc wykonać test Tukeya, aby dokładnie określić, które średnie grupowe są różne.

Krok 2: Wykonaj test Tukeya.

Poniższy kod pokazuje, jak używać funkcji TukeyHSD() do przeprowadzenia testu Tukeya:

 #perform Tukey's Test
TukeyHSD(model, conf.level= .95 ) 

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = values ~ group, data = data)

$group
         diff lwr upr p adj
BA 0.9777414 0.1979466 1.757536 0.0100545
CA 2.5454024 1.7656076 3.325197 0.0000000
CB 1.5676610 0.7878662 2.347456 0.0000199

Wartość p wskazuje, czy istnieje statystycznie istotna różnica pomiędzy każdym programem. Wyniki pokazują, że istnieje statystycznie istotna różnica pomiędzy średnią utratą masy ciała w każdym programie na poziomie istotności 0,05.

Zwłaszcza:

• Wartość P dla różnicy średnich między B i A: 0,0100545
• Wartość P dla różnicy średnich między C i A: 0,0000000
• Wartość P dla różnicy średnich między C i B: 0,0000199

Krok 3: Wizualizuj wyniki.

Możemy również użyć funkcji plot(TukeyHSD()) do wizualizacji przedziałów ufności:

 #plot confidence intervals
plot(TukeyHSD(model, conf.level= .95 ), las = 2 )

Uwaga: Argument las określa, że etykiety znaczników muszą być prostopadłe (las=2) do osi.

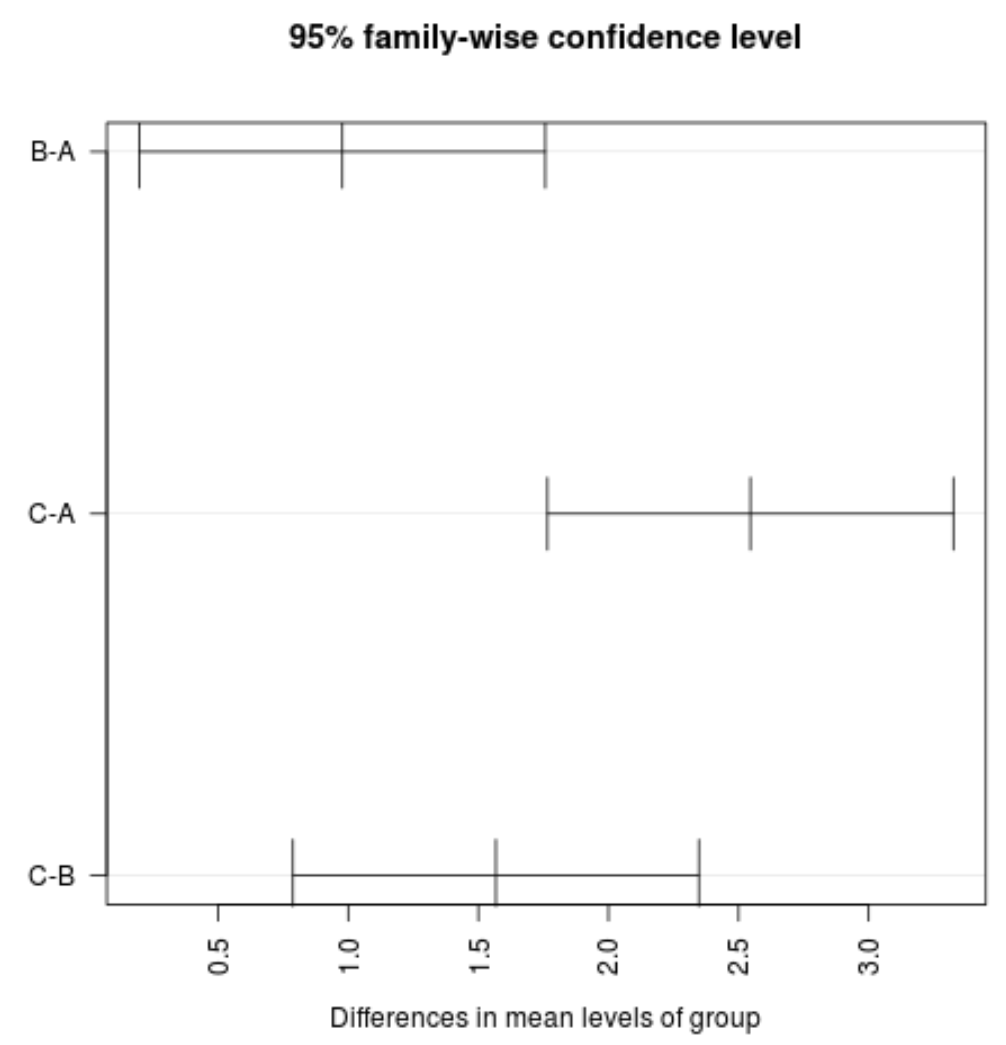
Widzimy, że żaden z przedziałów ufności dla wartości średniej pomiędzy grupami nie zawiera wartości zero, co wskazuje, że istnieje statystycznie istotna różnica w średniej stracie pomiędzy trzema grupami. Jest to zgodne z tym, że wszystkie wartości p dla naszych testów hipotez są mniejsze niż 0,05.

Dla tego konkretnego przykładu możemy stwierdzić, co następuje:

• Średnie wartości grupy C są znacznie wyższe niż średnie wartości grup A i B.
• Średnie wartości grupy B są znacznie wyższe niż średnie wartości grupy A.

Dodatkowe zasoby

Przewodnik po korzystaniu z testów post-hoc z ANOVA
Jak wykonać jednokierunkową ANOVA w R
Jak wykonać dwukierunkową ANOVA w R