Wykres punktowy
W tym artykule wyjaśniono, czym są wykresy punktowe. Dowiesz się zatem do czego służy chmura punktów, jak stworzyć chmurę punktów, jak ją interpretować oraz dowiesz się o przykładach chmur punktów.
Co to jest chmura punktów?
Wykres rozrzutu to rodzaj diagramu statystycznego, na którym zestaw danych składający się z dwóch zmiennych jest wykreślany na dwóch kartezjańskich osiach współrzędnych.
Dlatego do analizy związku między dwiema zmiennymi statystycznymi wykorzystuje się wykresy punktowe.
Wykresy rozrzutu mają kilka różnych nazw, takich jak diagram korelacji lub wykres rozrzutu .
Należy zaznaczyć, że diagram rozproszenia uważany jest za jedno z podstawowych narzędzi kontroli jakości, podobnie jak wykres Pareto, diagram przyczynowo-skutkowy, diagram blokowy itp.
Jak zrobić wykres punktowy
Aby utworzyć wykres punktowy, wykonaj następujące kroki:
- Zbierz dane statystyczne z próbki, którą chcesz poddać analizie. Należy pamiętać, że aby utworzyć wykres punktowy, muszą istnieć co najmniej dwie zmienne ilościowe.
- Narysuj dwie osie wykresu punktowego.
- Określ dwie zmienne statystyczne, które zostaną przedstawione na wykresie.
- Skalibruj skalę każdej osi wykresu. W tym celu zaleca się najpierw znaleźć minimum i maksimum każdej zmiennej i na podstawie tych wartości przeskalować każdą oś.
- Przedstaw każdą parę danych na wykresie punktowym.
- Przeanalizuj i zinterpretuj otrzymany diagram rozproszenia.
Przykład wykresu rozrzutu
Po zapoznaniu się z definicją diagramu punktowego i teorią jego tworzenia, w tej sekcji przedstawiono przykładowy diagram tego typu.
- W poniższej tabeli częstości zebrano jako dane wyniki z matematyki i statystyki próby 20 uczniów. Narysuj zbiór danych na wykresie rozrzutu i przeanalizuj go.
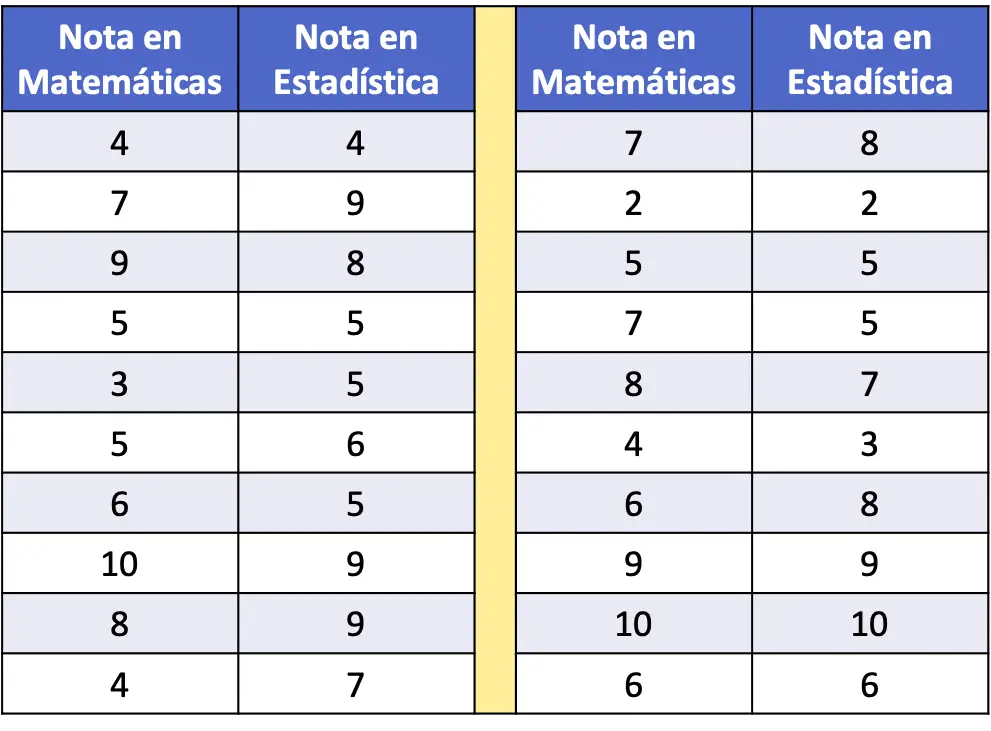
Aby przedstawić serie danych na wykresie punktowym, wystarczy wykreślić dwie osie, skalibrować je i wykreślić punkt na wykresie dla każdej pary danych. Pamiętaj, że punkt na wykresie umieszcza się na przecięciu wyimaginowanych linii odpowiadających każdej z jego wartości.
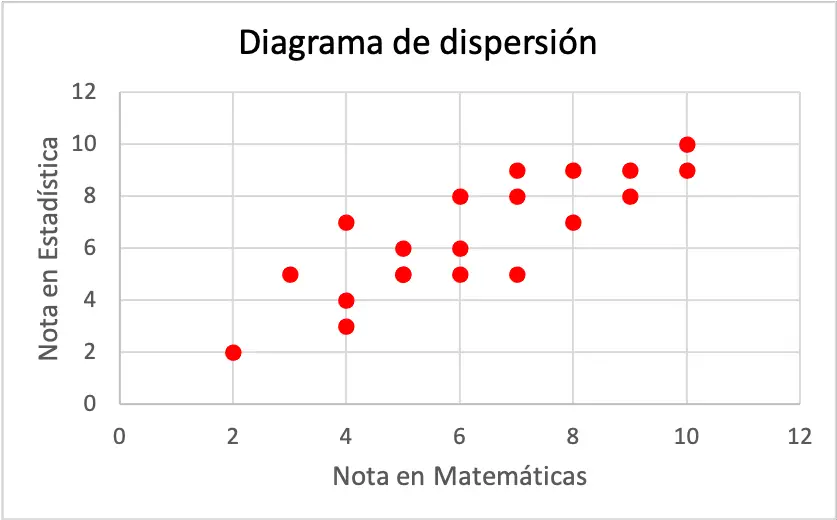
Każda oś wykresu punktowego reprezentuje zmienną. Dokładniej, oś pozioma należy do oceny uzyskanej z matematyki, natomiast oś pionowa odpowiada ocenie uzyskanej ze statystyki.
Jak widać na wykresie rozrzutu, obie zmienne mają dodatnią korelację, ponieważ jedna zmienna rośnie wraz ze wzrostem drugiej. Dlatego też stwierdza się, że jeśli uczeń uzyska lepszą ocenę z matematyki, jest bardziej prawdopodobne, że uzyska lepszą ocenę ze statystyki i odwrotnie.
Jednakże poprzedni wniosek nie oznacza, że jedna zmienna jest przyczyną drugiej, gdyż uzyskanie dobrej oceny z matematyki nie gwarantuje automatycznie dobrej oceny ze statystyki bez robienia czegokolwiek, a raczej należy uczyć się obu przedmiotów. W następnej sekcji zajmiemy się bardziej szczegółowo tą koncepcją.
Wykres punktowy i korelacja
Na podstawie diagramu punktowego można zidentyfikować rodzaj korelacji między dwiema zmiennymi:
- Korelacja bezpośrednia (lub korelacja dodatnia) : jedna zmienna wzrasta, gdy druga również rośnie.
- Korelacja odwrotna (lub korelacja ujemna) : gdy jedna zmienna rośnie, druga maleje i odwrotnie, jeśli jedna zmienna maleje, druga rośnie.
- Korelacja zerowa (Brak korelacji) : Nie ma związku pomiędzy tymi dwiema zmiennymi.
Podobnie, niezależnie od tego, czy korelacja między dwiema zmiennymi jest bezpośrednia czy odwrotna, korelację można również sklasyfikować na podstawie siły lub słabości związku między dwiema zmiennymi.
- Silna korelacja: obie zmienne są ze sobą ściśle powiązane. Punkty są gromadzone w chmurze punktów. Ułatwia to identyfikację zależności między zmiennymi.
- Niska korelacja : istnieje związek między dwiema zmiennymi, ale trudno go zidentyfikować. Punkty na chmurze punktów są daleko od siebie.

Z drugiej strony korelację można również obliczyć numerycznie za pomocą wzoru, co pozwala matematycznie określić, jak blisko powiązane są dwie różne zmienne. Aby zobaczyć jak to działa kliknij na poniższy link:
Należy pamiętać, że nawet jeśli istnieje korelacja między dwiema zmiennymi, nie oznacza to, że istnieje między nimi związek przyczynowy, tzn. korelacja między dwiema zmiennymi nie oznacza, że zmiana jednej zmiennej jest przyczyną zmiany drugiej. zmienny.
Tak więc, podobnie jak w przypadku wykresu rozrzutu w poprzedniej sekcji, chociaż istnieje dodatnia korelacja między oceną z matematyki a oceną ze statystyki, uzyskanie dobrej oceny z matematyki nie oznacza uzyskania dobrej oceny ze statystyki, ponieważ jeśli będziesz uczyć się tylko matematyki, na pewno nie uda ci się tego osiągnąć. w statystykach. Dlatego te dwie zmienne są ze sobą powiązane, ale nie są przyczyną i skutkiem.
Aby dowiedzieć się więcej, możesz kontynuować w następującym poście:
Zalety i wady chmury punktów
Ze względu na charakterystykę wykresu rozrzutu ten typ wykresu statystycznego ma zalety i wady.
Korzyść:
- Przedstawienie serii danych na wykresie punktowym jest dość proste.
- Wykres rozrzutu umożliwia wizualną analizę zależności pomiędzy dwiema zmiennymi, co ułatwia wyciąganie wniosków.
- Wykresy rozrzutu można również wykorzystać w dogłębnych badaniach statystycznych jako wstępną eksplorację danych.
Niedogodności:
- Diagramy tego typu nie są przydatne do przedstawiania zmiennych jakościowych.
- Interpretacja wykresu punktowego może prowadzić do błędnego wniosku o związku przyczynowo-skutkowym między dwiema zmiennymi.
- Wykresy rozrzutu nie pozwalają na analizę związku pomiędzy więcej niż dwiema zmiennymi.