Jak utworzyć macierz kowariancji w arkuszach google

Kowariancja jest miarą tego, jak zmiany jednej zmiennej są powiązane ze zmianami drugiej zmiennej. Mówiąc dokładniej, jest to miara stopnia, w jakim dwie zmienne są liniowo powiązane.

Wzór na obliczenie kowariancji pomiędzy dwiema zmiennymi, X i Y , wygląda następująco:

COV( X , Y ) = Σ(x- x )(y- y ) / n

Macierz kowariancji to macierz kwadratowa, która pokazuje kowariancję pomiędzy wieloma różnymi zmiennymi. Może to być przydatny sposób zrozumienia, w jaki sposób różne zmienne są powiązane w zbiorze danych.

Poniższy przykład pokazuje, jak utworzyć macierz kowariancji w Arkuszach Google dla danego zbioru danych.

Jak utworzyć macierz kowariancji w Arkuszach Google

Załóżmy, że mamy następujący zbiór danych, który pokazuje wyniki testów 10 różnych uczniów z trzech przedmiotów: matematyki, nauk ścisłych i historii.

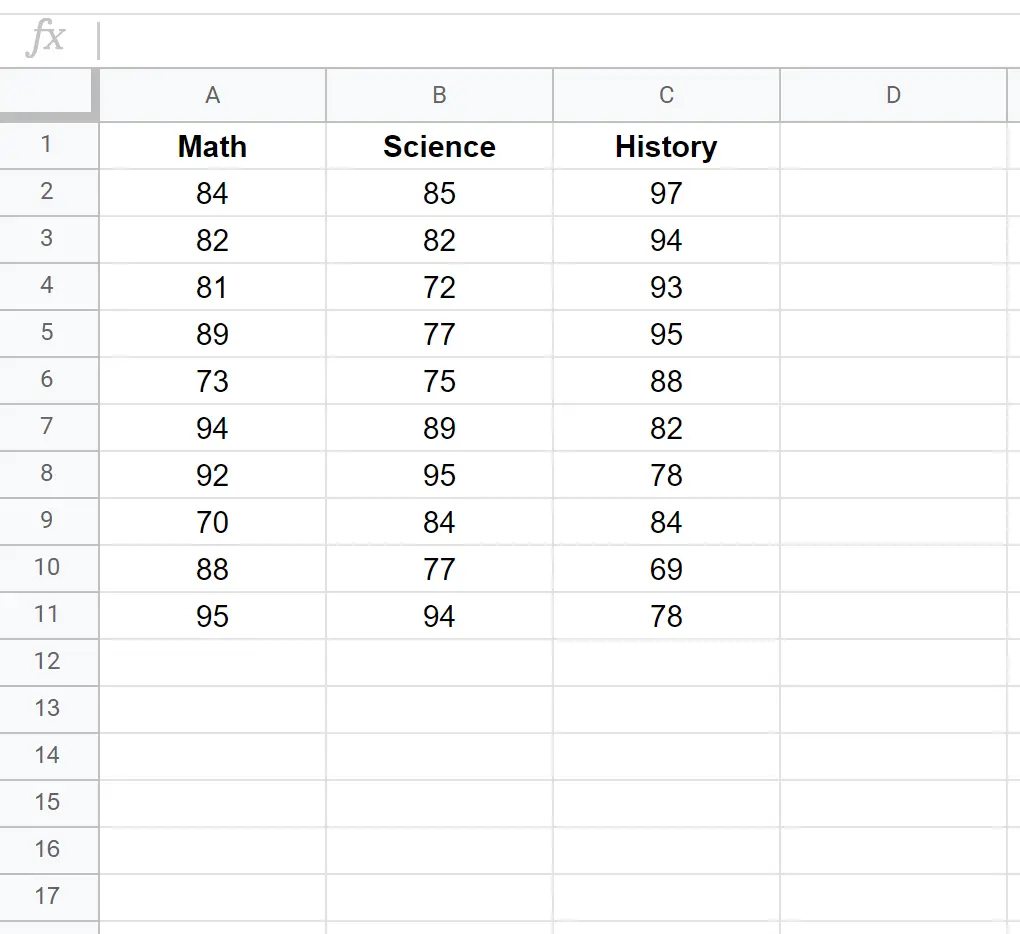
Aby utworzyć macierz kowariancji dla tego zbioru danych, możemy użyć funkcji COVAR() o następującej składni:

COVAR(dane_y, dane_x)

Macierz kowariancji dla tego zbioru danych jest pokazana w komórkach B15:D17 , natomiast formuły użyte do utworzenia macierzy kowariancji są pokazane w komórkach B21:D23 poniżej:

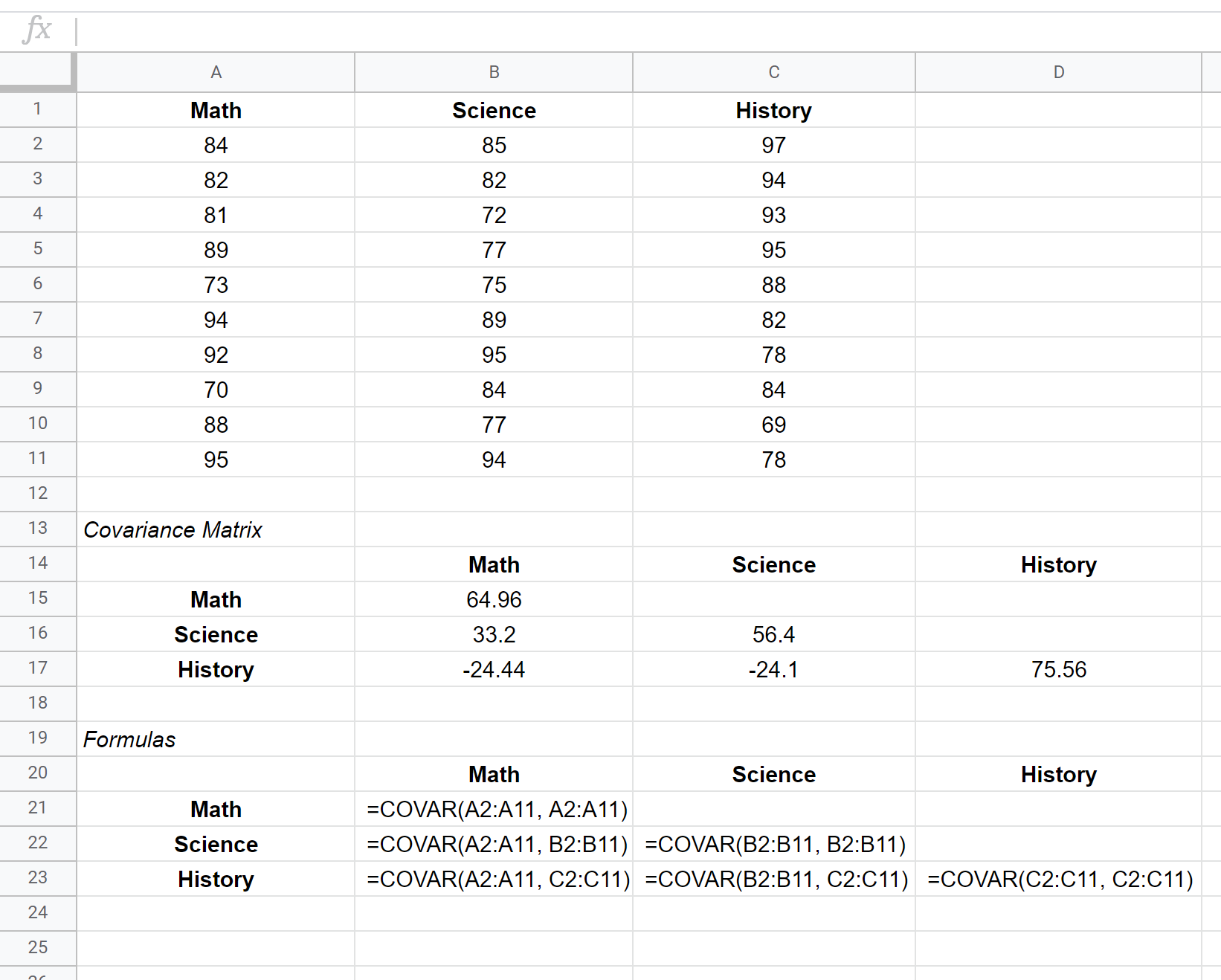
Jak interpretować macierz kowariancji

Kiedy już mamy macierz kowariancji, łatwo jest zinterpretować wartości macierzy.

Wartości wzdłuż przekątnych macierzy są po prostu wariancjami każdego przedmiotu. Na przykład:

• Wariancja wyników z matematyki wynosi 64,96
• Wariancja wyników z przedmiotów ścisłych wynosi 56,4
• Historyczna wariancja wyniku wynosi 75,56

Pozostałe wartości macierzy reprezentują kowariancje pomiędzy różnymi podmiotami. Na przykład:

• Kowariancja między wynikami z matematyki i przedmiotów ścisłych wynosi 33,2.
• Kowariancja między wynikami z matematyki i historii wynosi -24,44.
• Kowariancja między wynikami z nauk ścisłych i historii wynosi -24,1.

Dodatnia liczba kowariancji wskazuje, że dwie zmienne mają tendencję do wzrostu lub spadku w tandemie. Na przykład matematyka i przedmioty ścisłe mają dodatnią kowariancję (33,2), co wskazuje, że uczniowie, którzy uzyskują wysokie wyniki z matematyki, zwykle osiągają wysokie wyniki w przedmiotach ścisłych. Podobnie uczniowie, którzy osiągają słabe wyniki w matematyce, zwykle osiągają słabe wyniki w naukach ścisłych.

Ujemna liczba kowariancji wskazuje, że w miarę wzrostu jednej zmiennej druga zmienna ma tendencję do zmniejszania się. Na przykład matematyka i historia mają ujemną kowariancję (-24,44), co wskazuje, że uczniowie, którzy uzyskują wysokie wyniki z matematyki, zwykle uzyskują niskie wyniki z historii. Podobnie uczniowie, którzy osiągają niskie wyniki z matematyki, zwykle osiągają wysokie wyniki z historii.

Dodatkowe zasoby

Jak utworzyć macierz kowariancji w programie Excel
Jak utworzyć macierz kowariancji w R
Jak utworzyć macierz kowariancji w Pythonie
Jak utworzyć macierz kowariancji w SPSS