Jak obliczyć korelację rangi spearmana w arkuszach google

W statystyce korelacja odnosi się do siły i kierunku związku między dwiema zmiennymi. Wartość współczynnika korelacji może wynosić od -1 do 1, z następującymi interpretacjami:

• -1: doskonały negatywny związek między dwiema zmiennymi
• 0: brak związku pomiędzy dwiema zmiennymi
• 1: doskonały dodatni związek między dwiema zmiennymi

Specjalny rodzaj korelacji nazywany jest korelacją rang Spearmana i służy do pomiaru korelacji między dwiema zmiennymi rankingowymi. (na przykład ranga wyniku ucznia z egzaminu z matematyki w stosunku do rangi jego wyniku z egzaminu z przedmiotów ścisłych w klasie).

W tym samouczku wyjaśniono, jak obliczyć korelację rangi Spearmana między dwiema zmiennymi w Arkuszach Google.

Przykład: korelacja rangi Spearmana w Arkuszach Google

Wykonaj poniższe kroki, aby obliczyć korelację rangi Spearmana pomiędzy wynikami egzaminu z matematyki a wynikami egzaminu z przedmiotów ścisłych i przyrodniczych 10 uczniów w danej klasie.

Krok 1: Wprowadź dane.

Wprowadź wyniki egzaminu każdego ucznia w dwóch oddzielnych kolumnach:

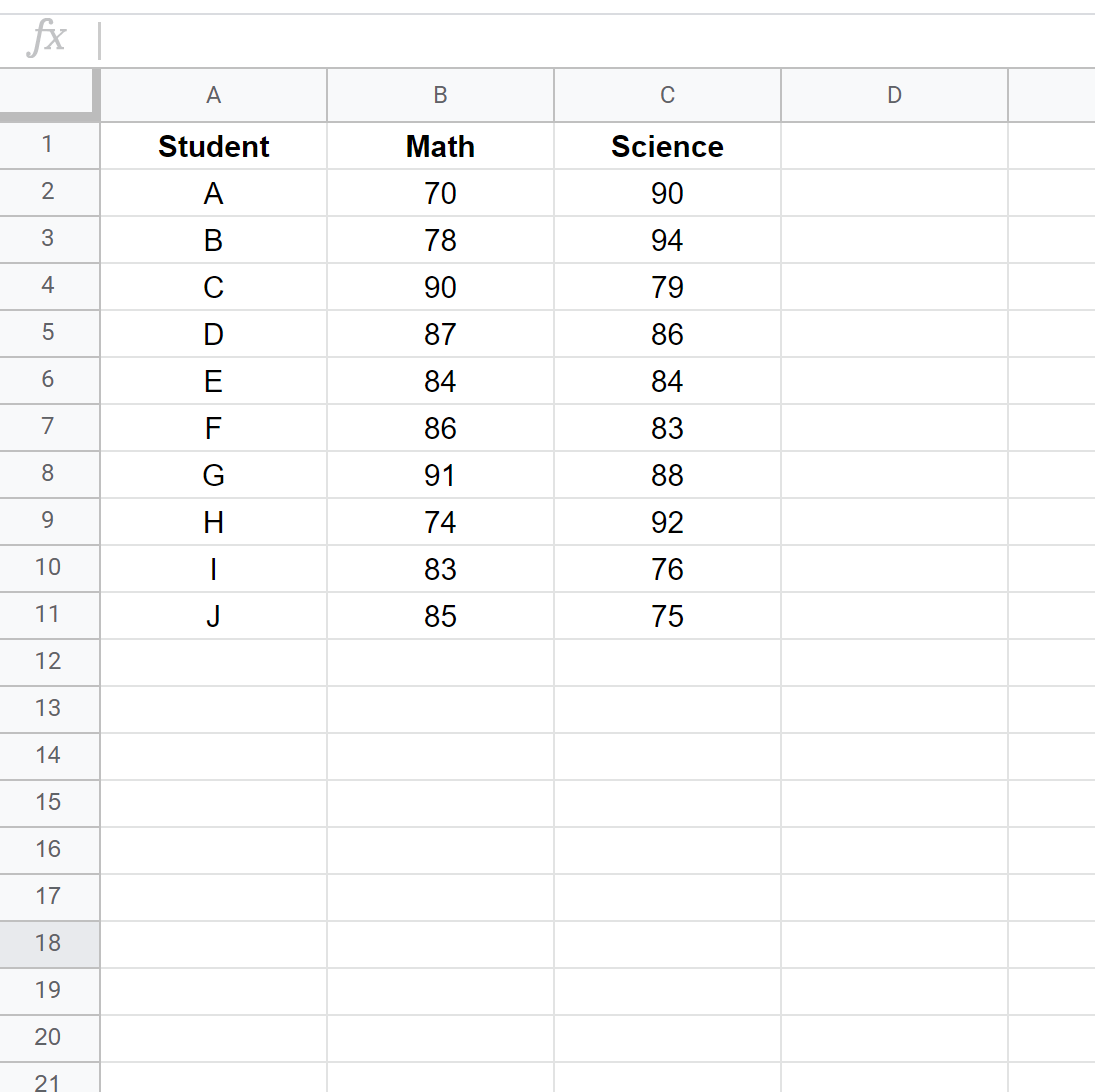
Krok 2: Oblicz rankingi dla każdego wyniku egzaminu.

Następnie obliczymy ranking dla każdego wyniku egzaminu. Użyj następujących wzorów w komórkach D2 i E2, aby obliczyć stopnie matematyczne i przyrodnicze pierwszego ucznia:

Komórka D2: =RANK.AVG(B2, $B$2:$B$11, 0)

Komórka E2: =RANK.AVG(C2, $C$2:$C$11, 0)

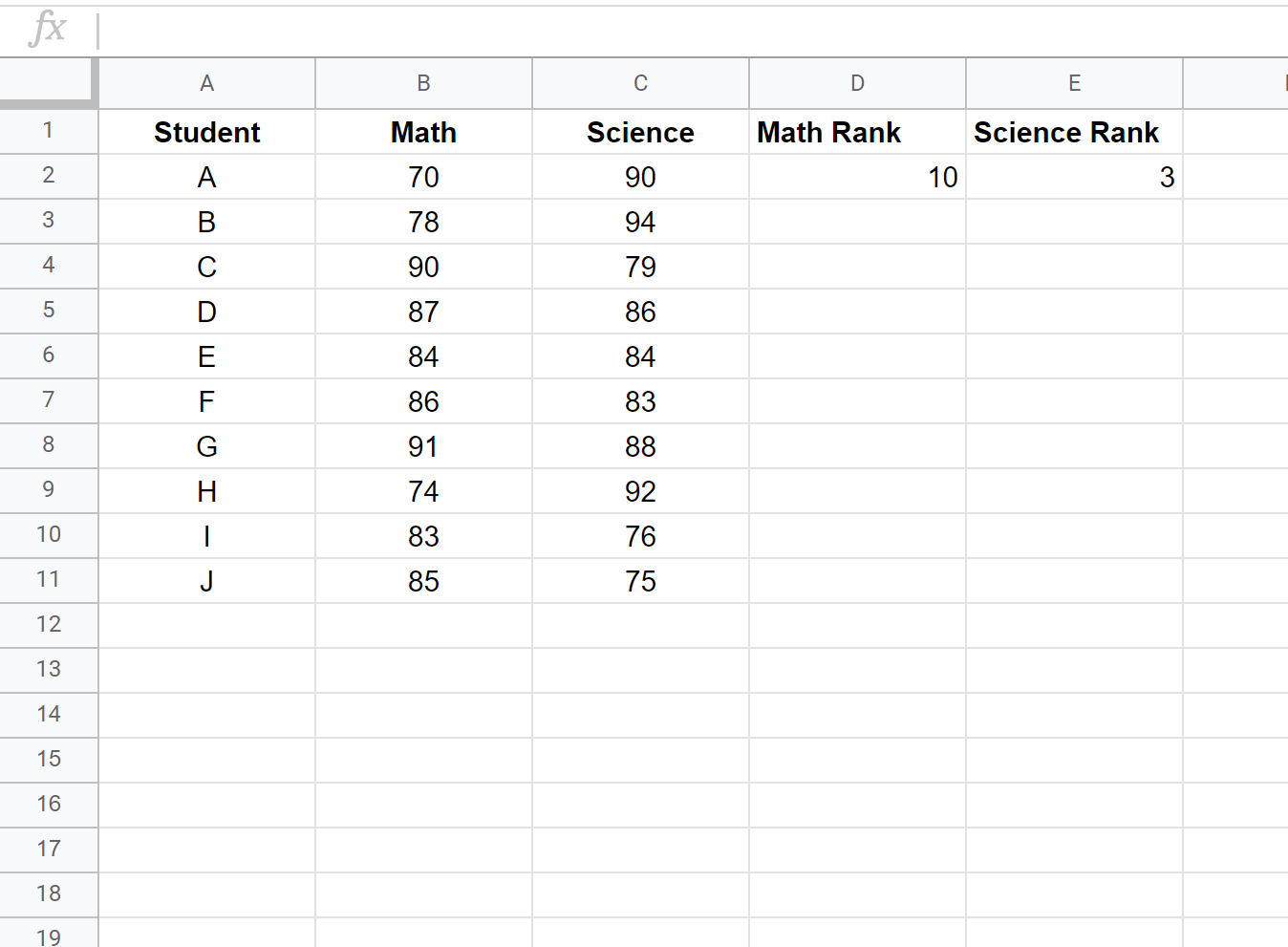
Następnie zaznacz pozostałe komórki do wypełnienia:

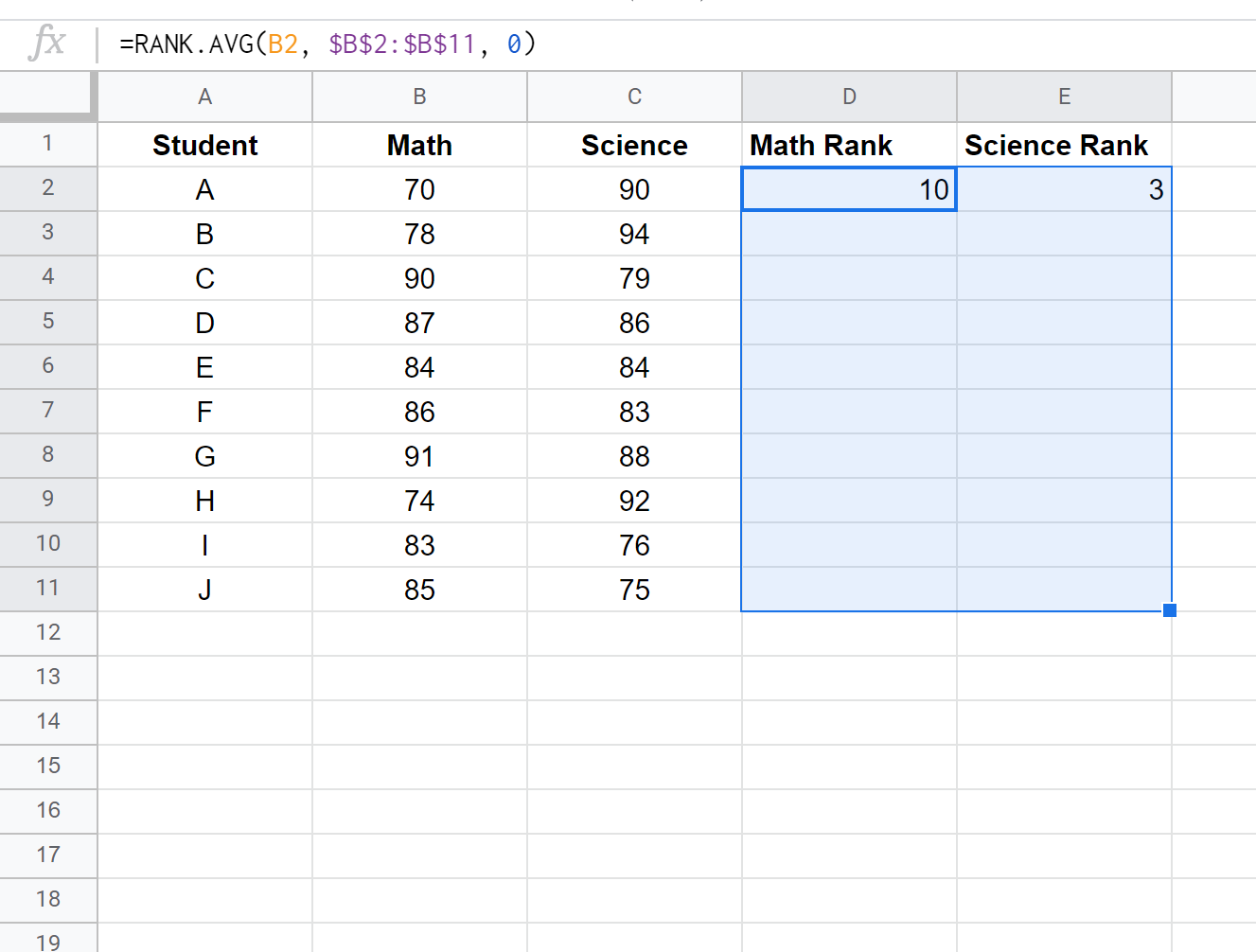
Następnie kliknij Ctrl+D, aby wprowadzić rankingi każdego ucznia:

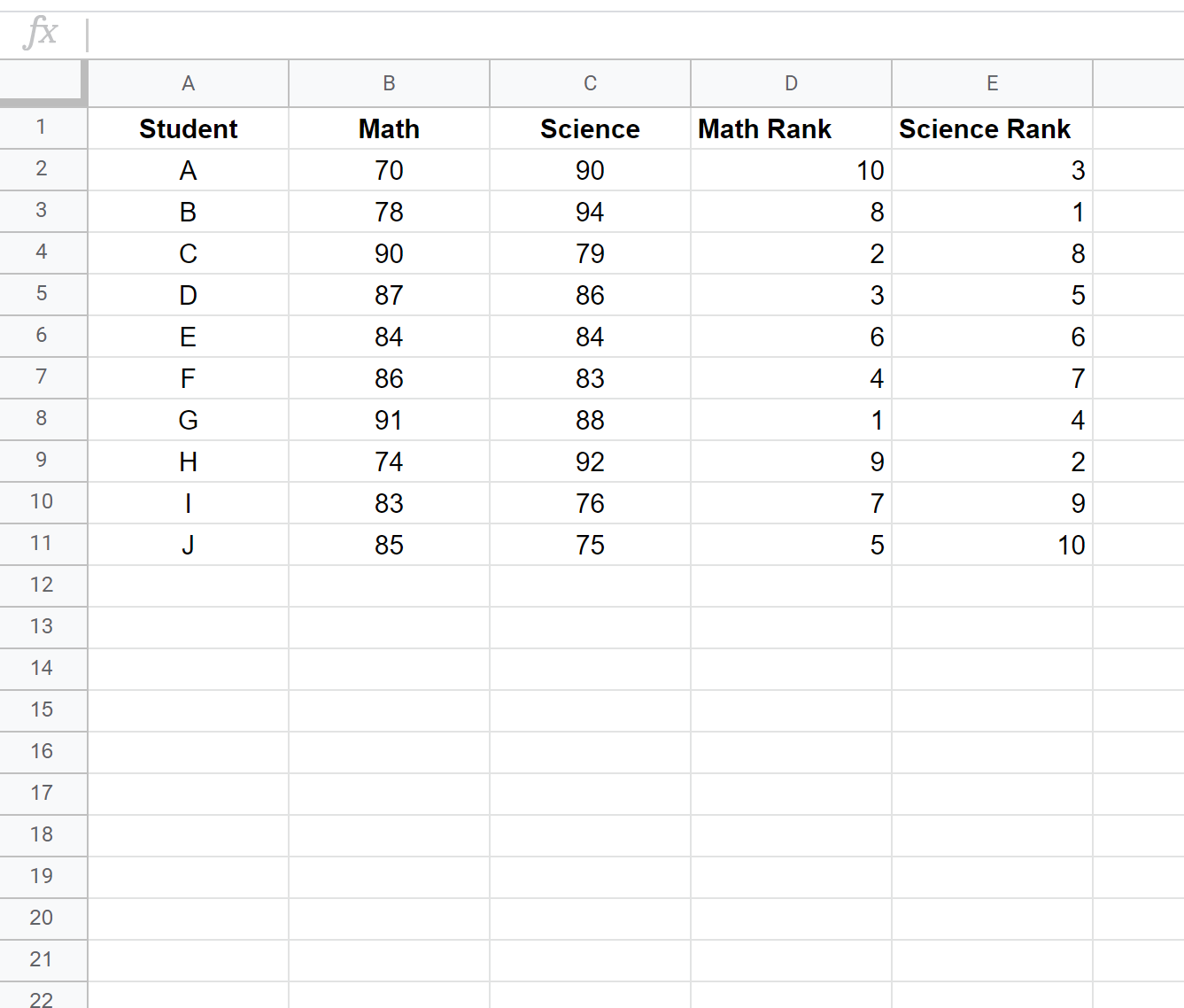
Krok 3: Oblicz współczynnik korelacji rang Spearmana.

Na koniec obliczymy współczynnik korelacji rangi Spearmana pomiędzy wynikami z matematyki a wynikami z przedmiotów ścisłych, korzystając z funkcji CORREL() :

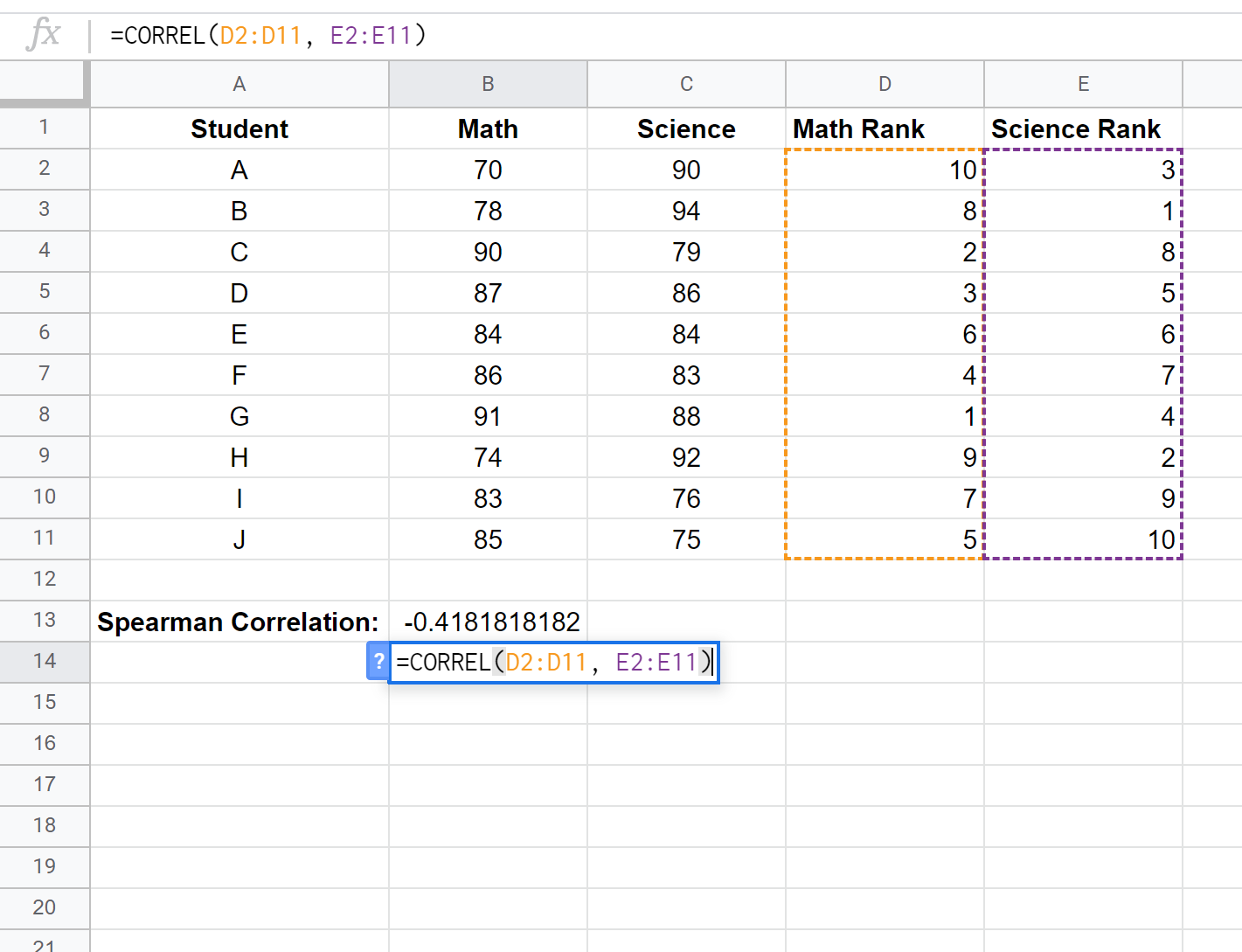
Korelacja rang Spearmana okazuje się wynosić -0,41818 .

Krok 4 (opcjonalnie): Określ, czy korelacja rang Spearmana jest istotna statystycznie.

W poprzednim kroku odkryliśmy, że korelacja rangi Spearmana między wynikami egzaminów z matematyki i przedmiotów ścisłych i przyrodniczych wyniosła -0,41818 , co wskazuje na ujemną korelację między obiema zmiennymi.

Aby jednak ustalić, czy korelacja ta jest istotna statystycznie, musielibyśmy odwołać się do tabeli korelacji rang Spearmana wartości krytycznych, która pokazuje wartości krytyczne powiązane z różnymi liczebnościami próbek (n) i poziomami istotności (α).

Jeżeli wartość bezwzględna naszego współczynnika korelacji jest większa od wartości krytycznej z tabeli, to korelacja pomiędzy obiema zmiennymi jest istotna statystycznie.

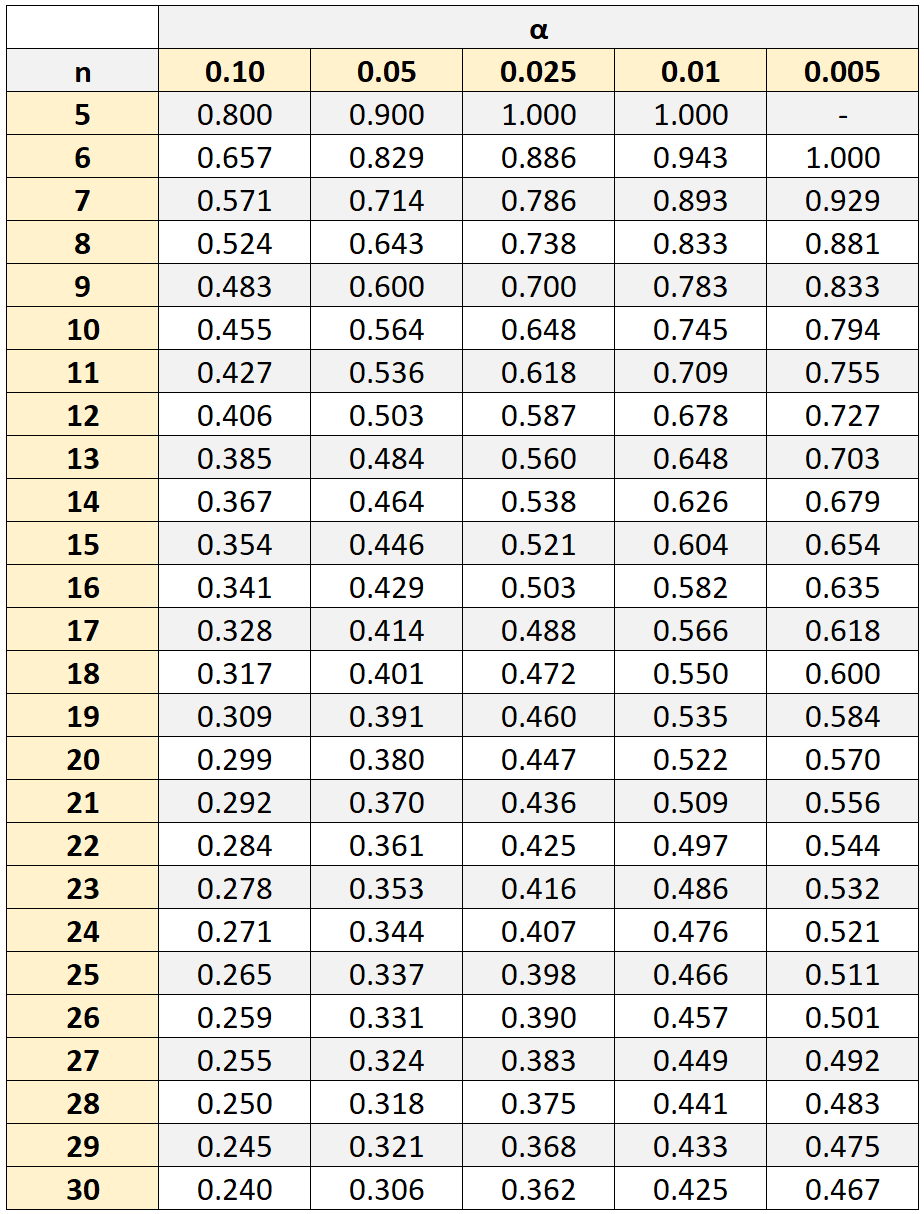
W naszym przykładzie wielkość próby wynosiła n = 10 uczniów. Stosując poziom istotności 0,05, stwierdzamy, że wartość krytyczna wynosi 0,564 .

Ponieważ wartość bezwzględna obliczonego przez nas współczynnika korelacji rang Spearmana ( 0,41818 ) nie jest większa niż ta wartość krytyczna, oznacza to, że korelacja między wynikami z matematyki i przedmiotów ścisłych nie jest istotna statystycznie.

Powiązane: Jak obliczyć korelację rangi Spearmana w programie Excel