Funkcja dystrybucyjna

Przez Benjamin Anderson 5 sierpnia, 2023 Prawdopodobieństwo 0 komentarzy

W tym artykule znajdziesz wyjaśnienie funkcji rozkładu, sposób obliczania jej wartości oraz rzeczywisty przykład funkcji rozkładu. Dodatkowo będziesz mógł zobaczyć różnice pomiędzy funkcją rozkładu a funkcją gęstości.

Jaka jest funkcja dystrybucji?

Funkcja dystrybucji , zwana także dystrybuantą , jest funkcją matematyczną wskazującą skumulowane prawdopodobieństwo dystrybucji. Oznacza to, że obraz funkcji rozkładu dla dowolnej wartości jest równy prawdopodobieństwu, że zmienna przyjmie tę wartość lub niższą wartość.

Do funkcji dystrybucji skumulowanej można także używać akronimu FDA, choć jej zwyczajowym symbolem jest duża litera F.

Funkcję rozkładu definiuje się zatem za pomocą następującego wzoru:

$F(x)=P[X\leq x]$

Jak obliczyć funkcję rozkładu

Następnie wyjaśnimy, jak obliczyć wartość funkcji rozkładu w zależności od tego, czy rozkład prawdopodobieństwa jest dyskretny, czy ciągły.

Dyskretne pudełko

Jeżeli zmienna losowa jest dyskretna, funkcja rozkładu skumulowanego jest równa sumie prawdopodobieństw wszystkich wartości równych lub mniejszych niż x .

$\displaystyle F(x)=P[X\leq x]=\sum_{u\leq x}f(u)$

Złoto

$f(u)$

jest funkcją prawdopodobieństwa powiązaną ze zmienną dyskretną.

Ciąg dalszy sprawy

Jeśli zmienna losowa jest ciągła, funkcja rozkładu skumulowanego jest równoważna całce funkcji gęstości od minus nieskończoności do danej wartości.

$\displaystyle F(x)=P[X\leq x]=\int_{-\infty}^{x}f(u)du$

Złoto

$f(u)$

jest funkcją gęstości powiązaną ze zmienną ciągłą.

Przykład funkcji rozkładu

Teraz, gdy znamy definicję funkcji rozkładu, spójrzmy na praktyczny przykład krok po kroku, aby dowiedzieć się, jak obliczyć wartość funkcji rozkładu.

Oblicz dystrybuantę losowego eksperymentu polegającego na czterokrotnym rzucie monetą.

Aby rozwiązać ćwiczenie, należy najpierw obliczyć wszystkie prawdopodobieństwa związane z liczbą orłów uzyskanych podczas czterech rzutów monetą:

prawdopodobieństwo rzucenia czterema monetami

Ponieważ jest to zmienna dyskretna, aby wyznaczyć obrazy funkcji rozkładu wystarczy dodać prawdopodobieństwa do wartości danej zmiennej:

$\begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}$

Zatem wartości rozkładu rzutu głową poprzez rzut czterema niezależnymi monetami są następujące:

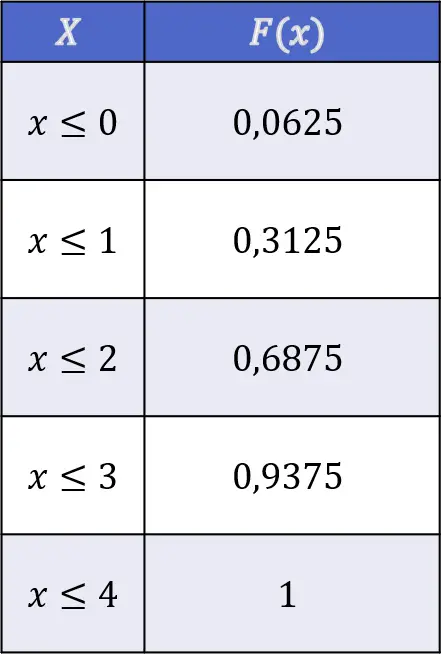
Własności funkcji rozkładu

Niezależnie od rodzaju zmiennej funkcja rozkładu ma zawsze następujące właściwości:

Wartość funkcji rozkładu skumulowanego mieści się w przedziale od 0 do 1 włącznie.

$0\leq F(x) \leq 1$

Granica funkcji rozkładu, gdy x dąży do nieskończoności, jest równa 1.

$\displaystyle\lim_{x\to +\infty} F(x)=1$

Z drugiej strony granica funkcji rozkładu, gdy x zbliża się do minus nieskończoności, wynosi zero.

$\displaystyle\lim_{x\to -\infty} F(x)=0$

Ze względu na swoją charakterystykę funkcja dystrybucji jest monotoniczna i niemalejąca.

$x_1 \leq x_2 \implies F(x_1)\leq F(x_2)$

Ponadto, jeśli
$a\leq b$

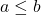
spełnione są następujące równania.

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

Funkcja rozkładu i funkcja gęstości

Na koniec zobaczymy, jaka jest różnica między funkcją rozkładu a funkcją gęstości, ponieważ te dwa pojęcia statystyczne są często mylone.

Różnica między dystrybuantą a funkcją gęstości to rodzaj definiowanego przez nie prawdopodobieństwa. Funkcja gęstości opisuje prawdopodobieństwo, że zmienna przyjmie określoną wartość, natomiast funkcja rozkładu opisuje skumulowane prawdopodobieństwo zmiennej.

Oznacza to, że funkcja rozkładu służy do obliczenia prawdopodobieństwa, że zmienna jest równa lub mniejsza od określonej wartości.

Należy zauważyć, że funkcja gęstości odnosi się tylko do zmiennych ciągłych, więc to rozróżnienie ma sens tylko wtedy, gdy badana zmienna jest ciągła.

Zwróć uwagę, jak zmienia się graficzna reprezentacja funkcji rozkładu w porównaniu z funkcją gęstości zmiennej, która ma rozkład normalny ze średnią 1 i odchyleniem standardowym 0,5:

różnica między funkcją rozkładu a funkcją gęstości

Więcej informacji na temat funkcji gęstości można znaleźć w następującym artykule:

➤ Zobacz: funkcja gęstości

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej