Jak utworzyć macierz korelacji w arkuszach google

Jednym ze sposobów ilościowego określenia związku między dwiema zmiennymi jest użycie współczynnika korelacji Pearsona , który jest miarą liniowego związku między dwiema zmiennymi . Ma wartość od -1 do 1, gdzie:

• -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
• Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
• 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi

Im współczynnik korelacji jest bardziej od zera, tym silniejszy jest związek między obiema zmiennymi.

Jednak w niektórych przypadkach chcemy zrozumieć korelację między wieloma parami zmiennych. W takich przypadkach możemy utworzyć macierz korelacji , która jest kwadratową tabelą pokazującą współczynniki korelacji pomiędzy kilkoma parami kombinacji zmiennych.

W tym samouczku wyjaśniono, jak utworzyć i zinterpretować macierz korelacji w Arkuszach Google.

Jak utworzyć macierz korelacji w Arkuszach Google

Załóżmy, że mamy następujący zestaw danych, który pokazuje średnią liczbę punktów, zbiórek i asyst dla 10 koszykarzy:

Aby utworzyć macierz korelacji dla tego zbioru danych, możemy użyć funkcji CORREL() o następującej składni:

  COVAR(dane_y, dane_x)

Macierz kowariancji dla tego zbioru danych jest pokazana w komórkach B15:D17 , natomiast formuły użyte do utworzenia macierzy kowariancji są pokazane w komórkach B21:D23 poniżej:

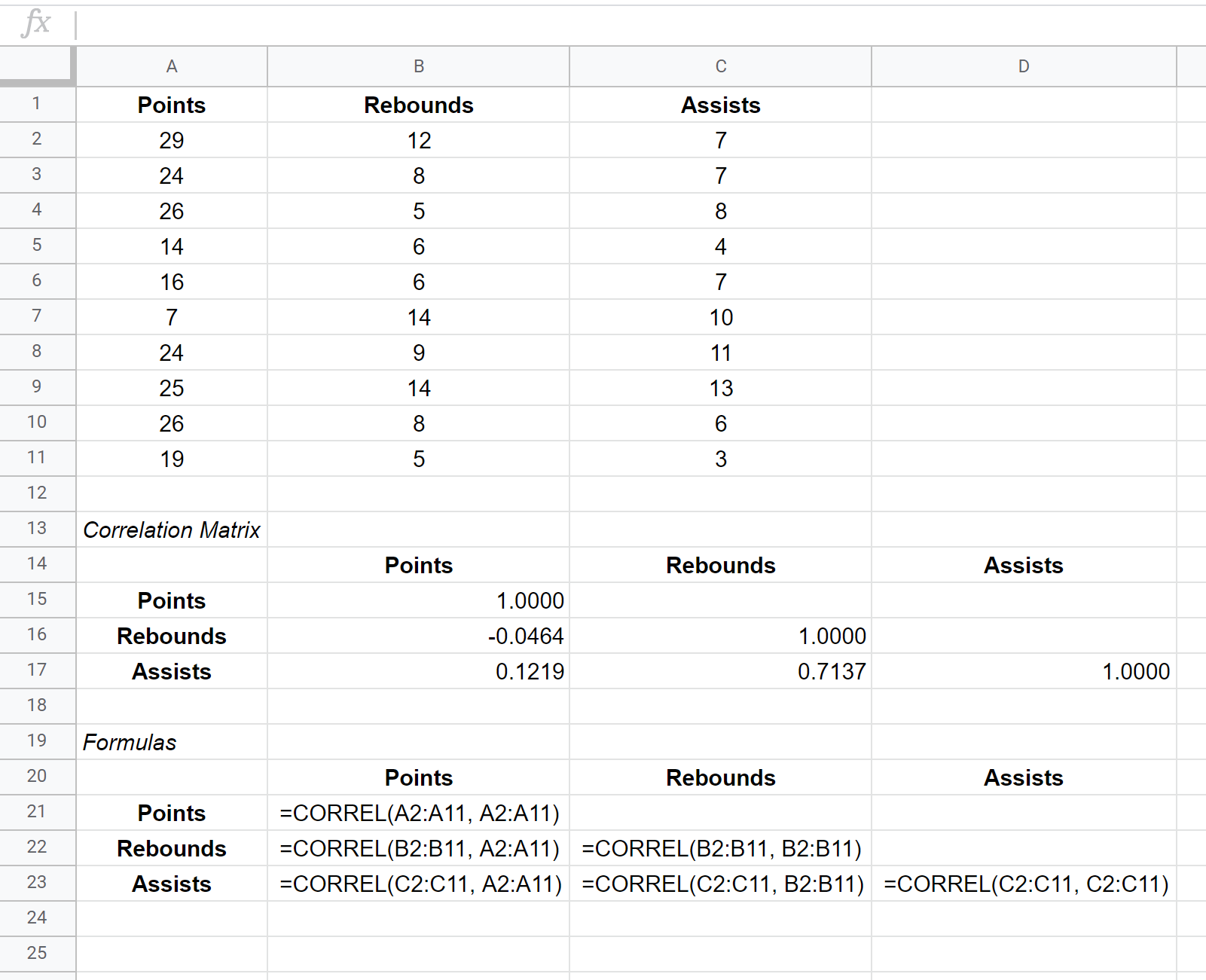
Jak interpretować macierz korelacji

Wartości w poszczególnych komórkach macierzy korelacji informują nas o współczynniku korelacji Pearsona pomiędzy każdą parą kombinacji zmiennych. Na przykład:

Korelacja punktów i zbiórek: -0,0464. Punkty i zbiórki są nieco ujemnie skorelowane, ale wartość ta jest tak bliska zeru, że nie ma mocnych dowodów na istotny związek między tymi dwiema zmiennymi.

Korelacja punktów i asyst: 0,1219. Punkty i asysty są nieco dodatnio skorelowane, ale wartość ta jest również dość bliska zeru, więc nie ma mocnych dowodów na istotny związek między tymi dwiema zmiennymi.

Korelacja między zbiórkami i asystami: 0,7137. Zbiórki i asysty są silnie dodatnio skorelowane. Oznacza to, że gracze, którzy mają więcej zbiórek, mają również zwykle więcej asyst.

Należy zauważyć, że wszystkie wartości diagonalne macierzy korelacji wynoszą 1, ponieważ korelacja między zmienną a nią samą wynosi zawsze 1. W praktyce liczba ta nie jest przydatna do interpretacji.

Dodatkowe zasoby

Jak czytać macierz korelacji
Jak utworzyć macierz korelacji w programie Excel