Jak wykonać regresję liniową w arkuszach google

Regresja liniowa to metoda, którą można zastosować do ilościowego określenia związku między jedną lub większą liczbą zmiennych objaśniających a zmienną odpowiedzi .

Stosujemy prostą regresję liniową, gdy istnieje tylko jedna zmienna objaśniająca, i wielokrotną regresję liniową, gdy istnieją dwie lub więcej zmiennych objaśniających.

Obydwa typy regresji można wykonać za pomocą funkcji LINEST() Arkuszy Google, która wykorzystuje następującą składnię:

REGLINP (znane_dane_y, znane_dane_x, oblicz_b, pełne)

Złoto:

• znane_dane_y: tablica wartości odpowiedzi
• znane_dane_x: Tabela wartości objaśniających
• oblicz_b: wskazuje, czy obliczyć wyraz wolny. Domyślnie jest to PRAWDA i pozostawiamy to w przypadku regresji liniowej.
• szczegółowe: Wskazuje, czy zapewnić dodatkowe statystyki regresji poza samym nachyleniem i przecięciem. Domyślnie jest to FAŁSZ, ale w naszych przykładach określimy, że jest to PRAWDA.

Poniższe przykłady pokazują, jak w praktyce wykorzystać tę funkcję.

Prosta regresja liniowa w Arkuszach Google

Załóżmy, że chcemy zrozumieć związek pomiędzy przepracowanymi godzinami a wynikami egzaminów. przygotowanie się do egzaminu i uzyskaną na nim ocenę.

Aby zbadać tę zależność, możemy przeprowadzić prostą regresję liniową, wykorzystując przestudiowane godziny jako zmienną objaśniającą i wyniki egzaminów jako zmienną odpowiedzi.

Poniższy zrzut ekranu pokazuje, jak wykonać prostą regresję liniową przy użyciu zestawu danych 20 uczniów z następującym wzorem zastosowanym w komórce D2:

= LINIA ( B2:B21 , A2:A21 , PRAWDA , PRAWDA )

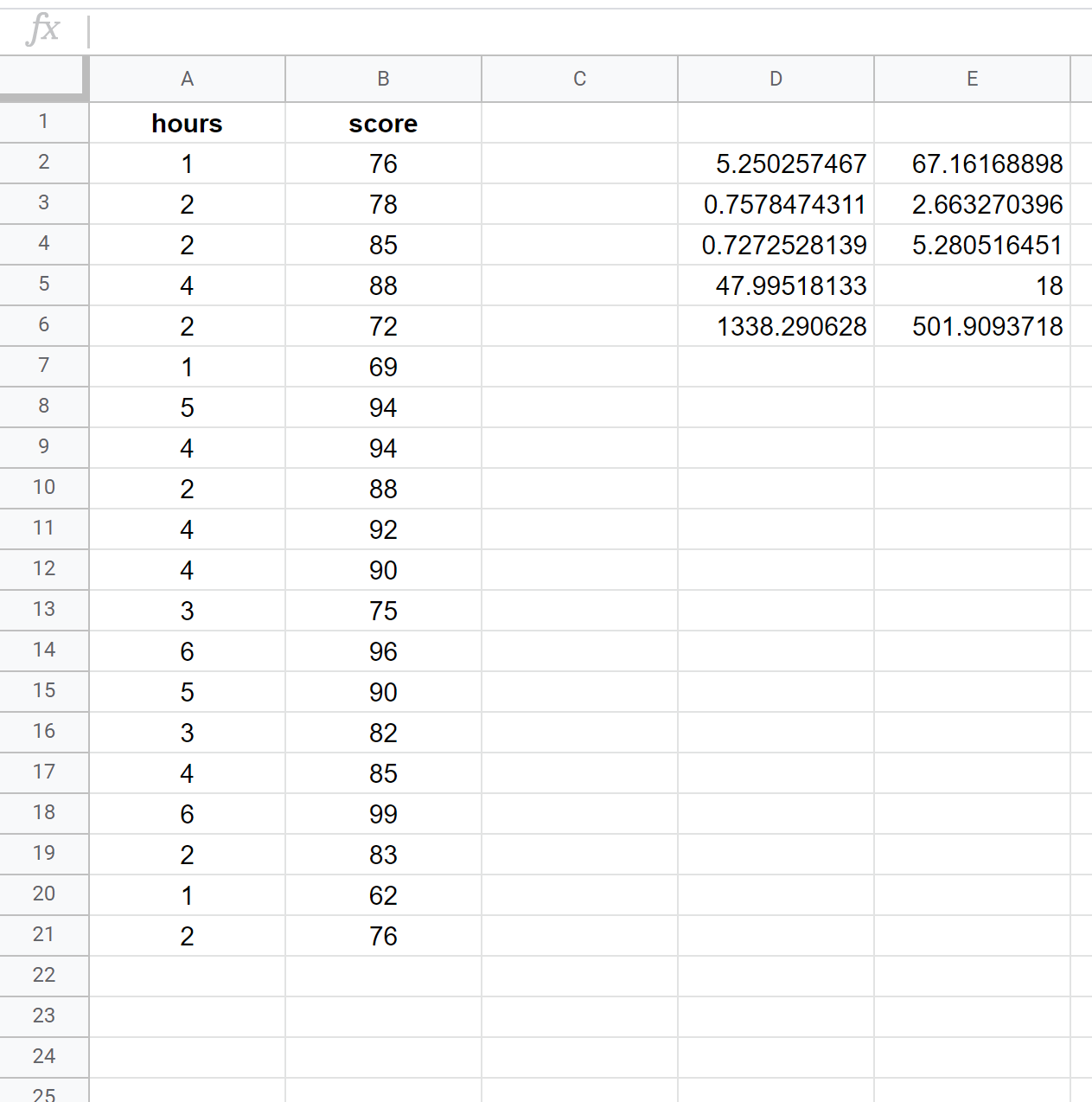
Poniższy zrzut ekranu zawiera adnotacje dotyczące danych wyjściowych:

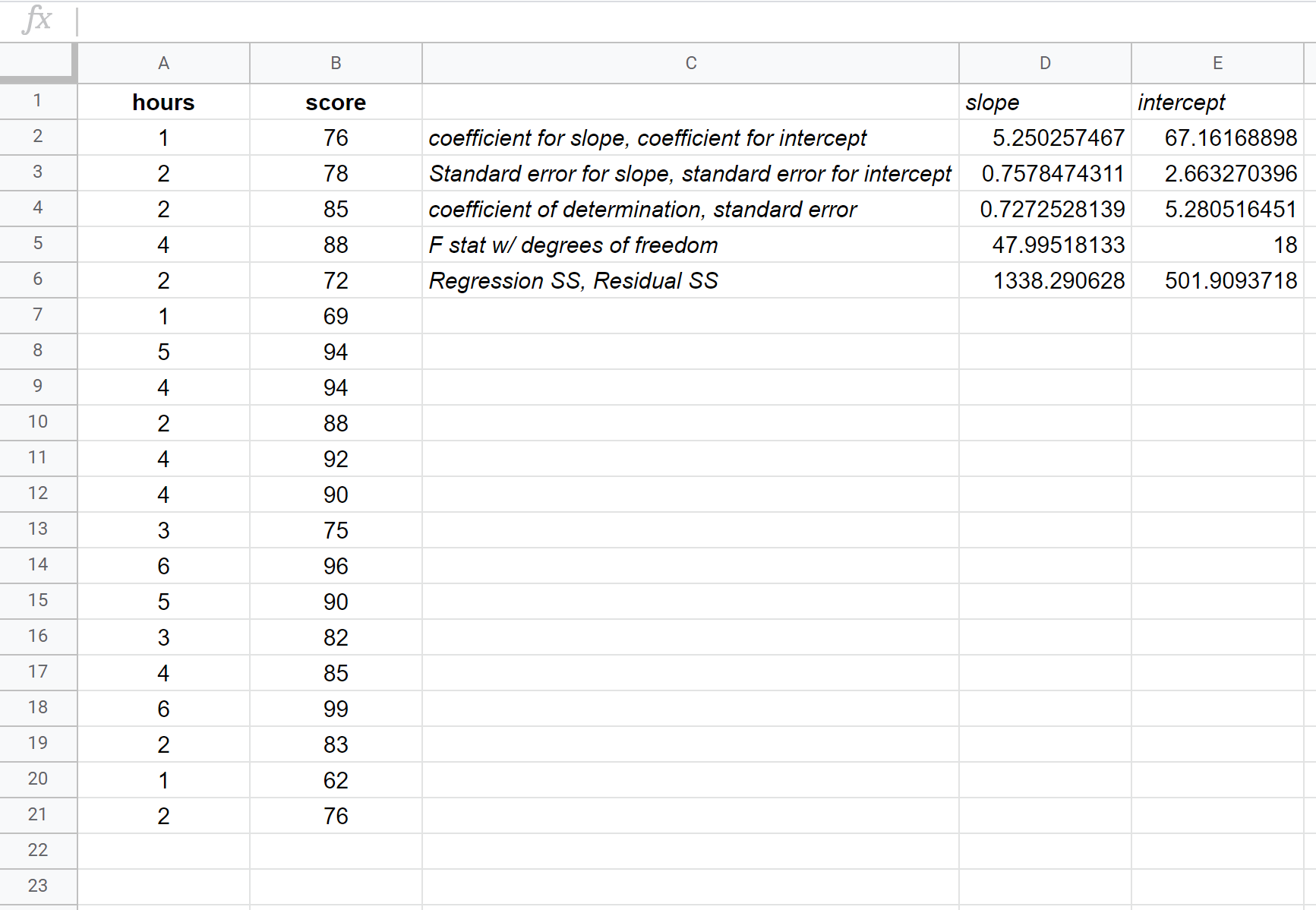
Oto jak zinterpretować najbardziej odpowiednie liczby w wyniku:

R Kwadrat: 0,72725 . Nazywa się to współczynnikiem determinacji. Jest to proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennej objaśniającej. W tym przykładzie około 72,73% różnic w wynikach egzaminów można wyjaśnić liczbą godzin nauki.

Błąd standardowy: 5.2805 . Jest to średnia odległość pomiędzy obserwowanymi wartościami a linią regresji. W tym przykładzie zaobserwowane wartości odbiegają średnio o 5,2805 jednostki od linii regresji.

Współczynniki: Współczynniki dają nam liczby potrzebne do napisania oszacowanego równania regresji. W tym przykładzie oszacowane równanie regresji wygląda następująco:

Wynik egzaminu = 67,16 + 5,2503*(godziny)

Współczynnik godzin interpretujemy w ten sposób, że za każdą dodatkową przestudiowaną godzinę wynik egzaminu powinien wzrosnąć średnio o 5,2503 . Interpretujemy współczynnik wyrazu tak, że oczekiwany wynik egzaminu dla studenta studiującego zero godzin wynosi 67,16 .

Możemy użyć tego szacunkowego równania regresji do obliczenia oczekiwanego wyniku egzaminu dla studenta na podstawie liczby godzin nauki. Na przykład student studiujący trzy godziny powinien uzyskać wynik egzaminu 82,91 :

Wynik egzaminu = 67,16 + 5,2503*(3) = 82,91

Wielokrotna regresja liniowa w Arkuszach Google

Załóżmy, że chcemy wiedzieć, czy liczba godzin spędzonych na nauce i liczba zdanych egzaminów przygotowawczych wpływają na ocenę, jaką student otrzymuje z określonego egzaminu wstępnego na studia.

Aby zbadać tę zależność, możemy przeprowadzić wielokrotną regresję liniową, wykorzystując przepracowane godziny i egzaminy przygotowawcze traktowane jako zmienne objaśniające, a wyniki egzaminów jako zmienną odpowiedzi.

Poniższy zrzut ekranu pokazuje, jak przeprowadzić wielokrotną regresję liniową przy użyciu zestawu danych 20 uczniów z następującą formułą zastosowaną w komórce E2:

= PRAWO ( C2:C21 , A2:B21 , PRAWDA , PRAWDA )

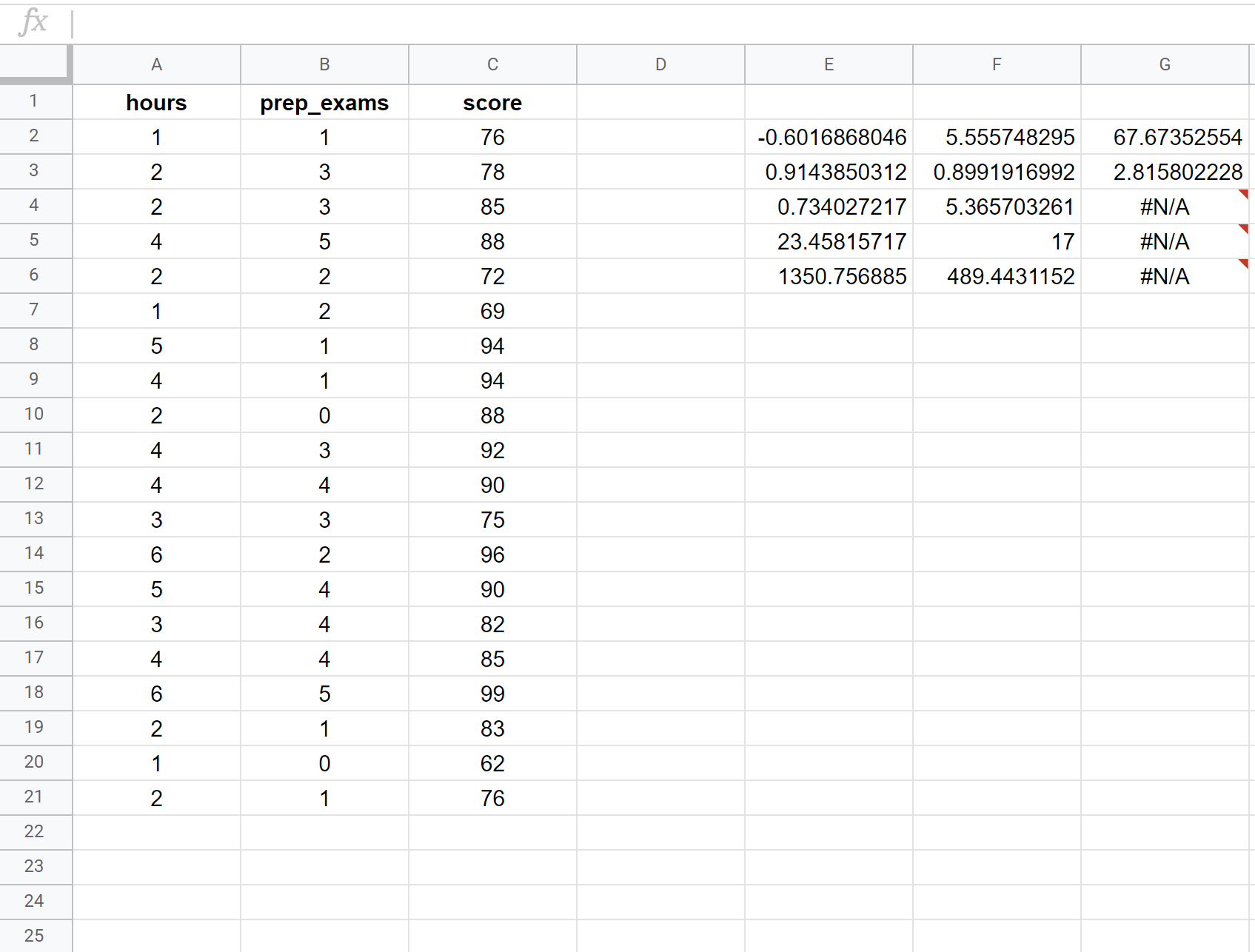
Oto jak zinterpretować najbardziej odpowiednie liczby w wyniku:

R Kwadrat: 0,734 . Nazywa się to współczynnikiem determinacji. Jest to proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennych objaśniających. W tym przykładzie 73,4% różnic w wynikach egzaminów można wytłumaczyć liczbą godzin nauki i liczbą zdanych egzaminów przygotowawczych.

Błąd standardowy: 5,3657 . Jest to średnia odległość pomiędzy obserwowanymi wartościami a linią regresji. W tym przykładzie zaobserwowane wartości odbiegają średnio o 5,3657 jednostki od linii regresji.

Szacowane równanie regresji: Możemy użyć współczynników z wyników modelu, aby utworzyć następujące szacunkowe równanie regresji:

Wynik egzaminu = 67,67 + 5,56*(godziny) – 0,60*(egzamin przygotowawczy)

Możemy użyć tego szacunkowego równania regresji do obliczenia oczekiwanego wyniku egzaminu dla studenta na podstawie liczby godzin nauki i liczby egzaminów praktycznych, które zdają. Przykładowo, student studiujący trzy godziny i przystępujący do egzaminu przygotowawczego powinien otrzymać ocenę 83,75 :

Wynik egzaminu = 67,67 + 5,56*(3) – 0,60*(1) = 83,75

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w Arkuszach Google:

Jak wykonać regresję wielomianową w Arkuszach Google
Jak utworzyć wykres resztkowy w Arkuszach Google