Jak przekształcać dane w r (log, pierwiastek kwadratowy, pierwiastek sześcienny)

Wiele testów statystycznych zakłada, że reszty zmiennej odpowiedzi mają rozkład normalny.

Jednakże reszty często nie mają rozkładu normalnego. Jednym ze sposobów rozwiązania tego problemu jest przekształcenie zmiennej odpowiedzi za pomocą jednej z trzech transformacji:

1. Transformacja logu: przekształć zmienną odpowiedzi z y na log(y) .

2. Transformacja pierwiastka kwadratowego: Przekształć zmienną odpowiedzi z y na √y .

3. Transformacja pierwiastka sześciennego: przekształć zmienną odpowiedzi z y na y ^1/3 .

Wykonując te przekształcenia, zmienna odpowiedzi ogólnie zbliża się do rozkładu normalnego. Poniższe przykłady pokazują, jak wykonać te przekształcenia w R.

Transformacja dziennika w R

Poniższy kod pokazuje, jak wykonać transformację logu zmiennej odpowiedzi:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform log transformation
log_y <- log10(df$y)

Poniższy kod pokazuje, jak utworzyć histogramy wyświetlające rozkład y przed i po wykonaniu transformacji logarytmicznej:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for log-transformed distribution 
hist(log_y, col='coral2', main='Log Transformed')

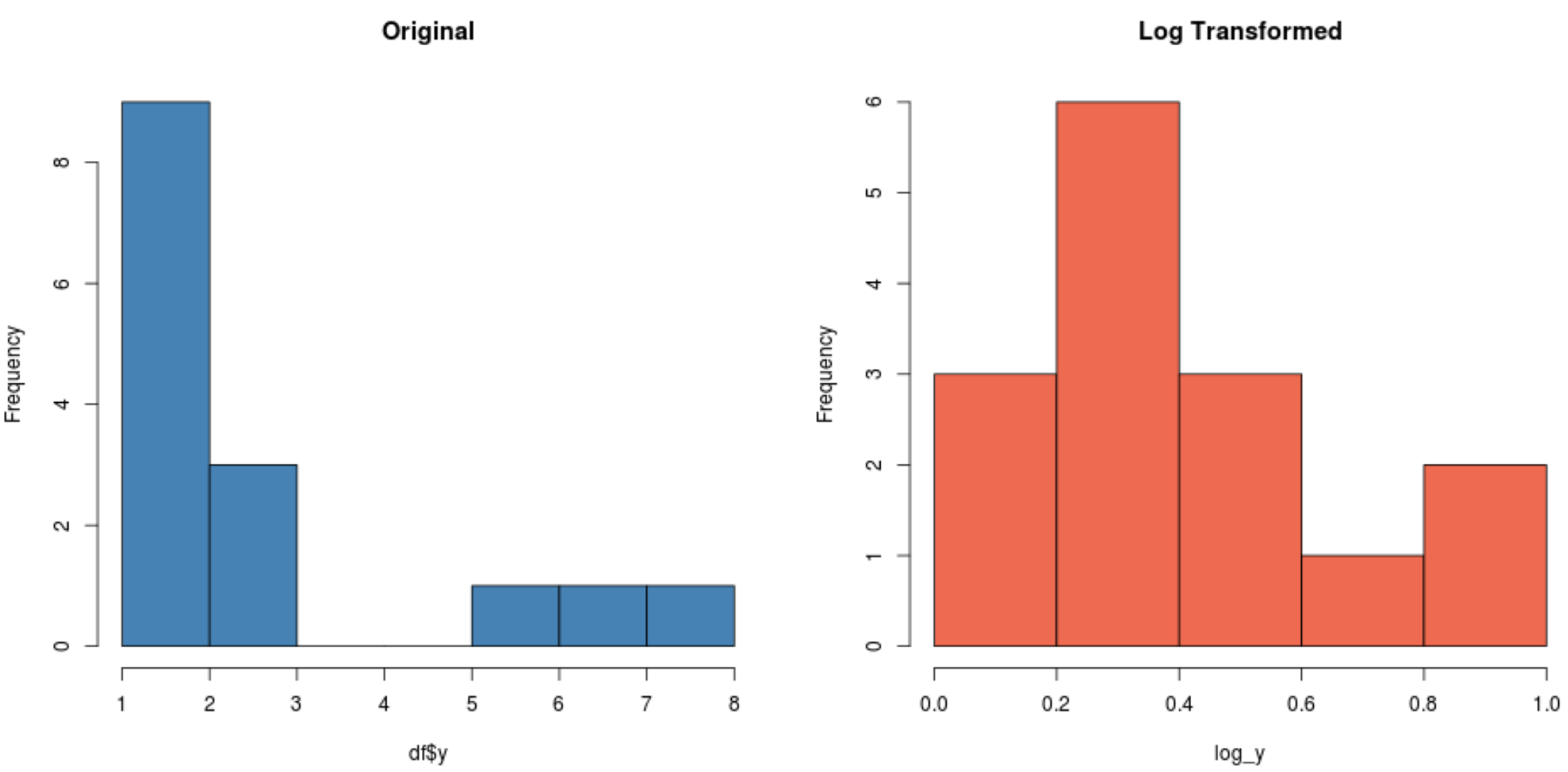
Zwróć uwagę, że rozkład przekształcony logarytmicznie jest znacznie bardziej normalny niż rozkład pierwotny. Nadal nie jest to idealny „kształt dzwonu”, ale jest bliższy rozkładowi normalnemu niż rozkładowi pierwotnemu.

W rzeczywistości, jeśli wykonamytest Shapiro-Wilka dla każdego rozkładu, odkryjemy, że pierwotny rozkład nie spełnia założenia normalności, podczas gdy rozkład przekształcony logarytmicznie nie spełnia tego założenia (przy α = 0,05):

 #perform Shapiro-Wilk Test on original data
shapiro.test(df$y)

	Shapiro-Wilk normality test

data: df$y
W = 0.77225, p-value = 0.001655

#perform Shapiro-Wilk Test on log-transformed data 
shapiro.test(log_y)

	Shapiro-Wilk normality test

data:log_y
W = 0.89089, p-value = 0.06917

Transformacja pierwiastka kwadratowego w R

Poniższy kod pokazuje, jak wykonać transformację pierwiastka kwadratowego zmiennej odpowiedzi:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
sqrt_y <- sqrt(df$y)

Poniższy kod pokazuje, jak utworzyć histogramy wyświetlające rozkład y przed i po wykonaniu transformacji pierwiastkowej:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(sqrt_y, col='coral2', main='Square Root Transformed') 

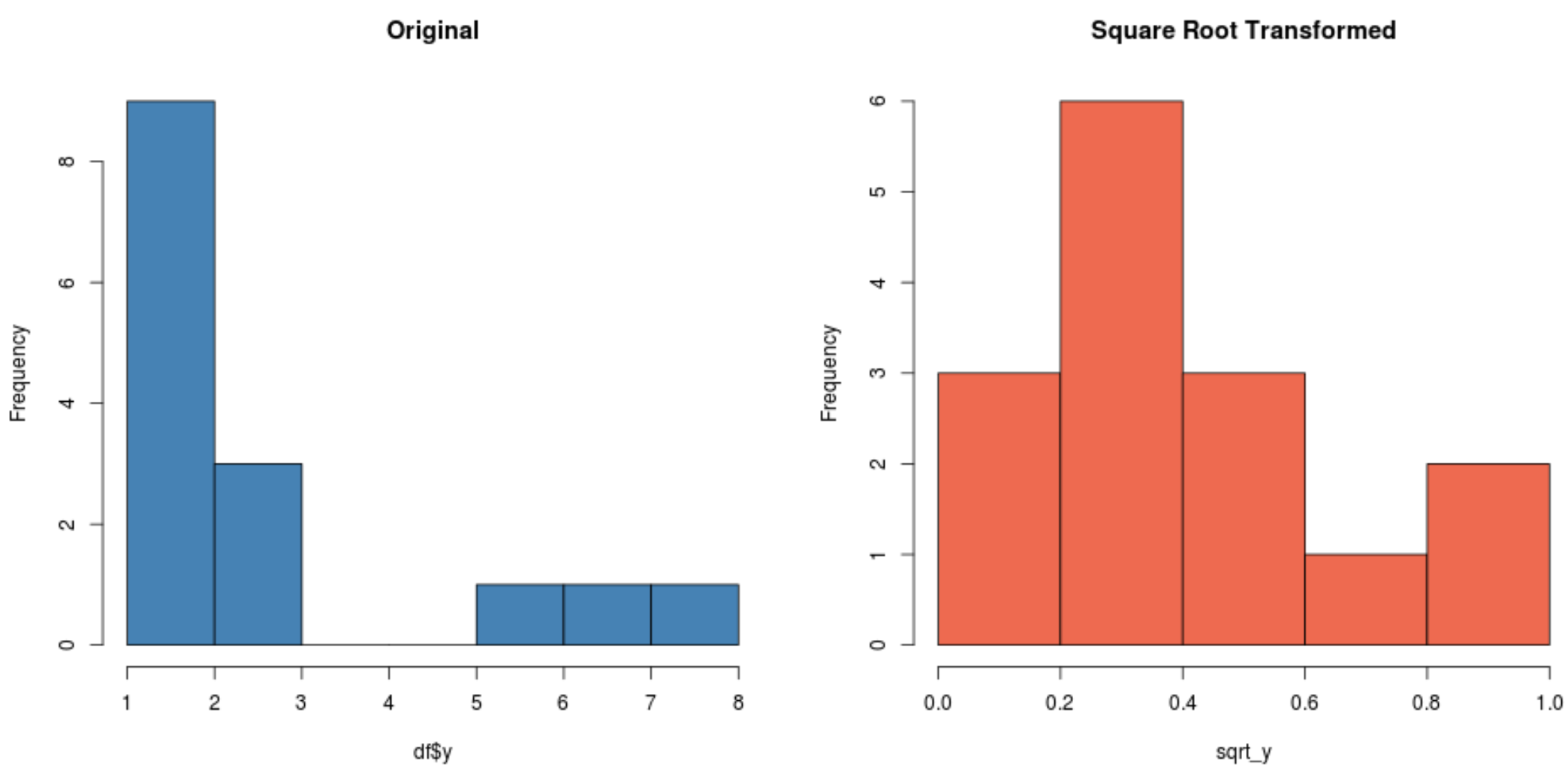
Zwróć uwagę, że rozkład przekształcony w pierwiastek kwadratowy ma znacznie bardziej rozkład normalny niż rozkład pierwotny.

Transformacja pierwiastka sześciennego w R

Poniższy kod pokazuje, jak przeprowadzić transformację pierwiastka sześciennego na zmiennej odpowiedzi:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
cube_y <- df$y^(1/3)

Poniższy kod pokazuje, jak utworzyć histogramy wyświetlające rozkład y przed i po wykonaniu transformacji pierwiastkowej:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(cube_y, col='coral2', main='Cube Root Transformed') 

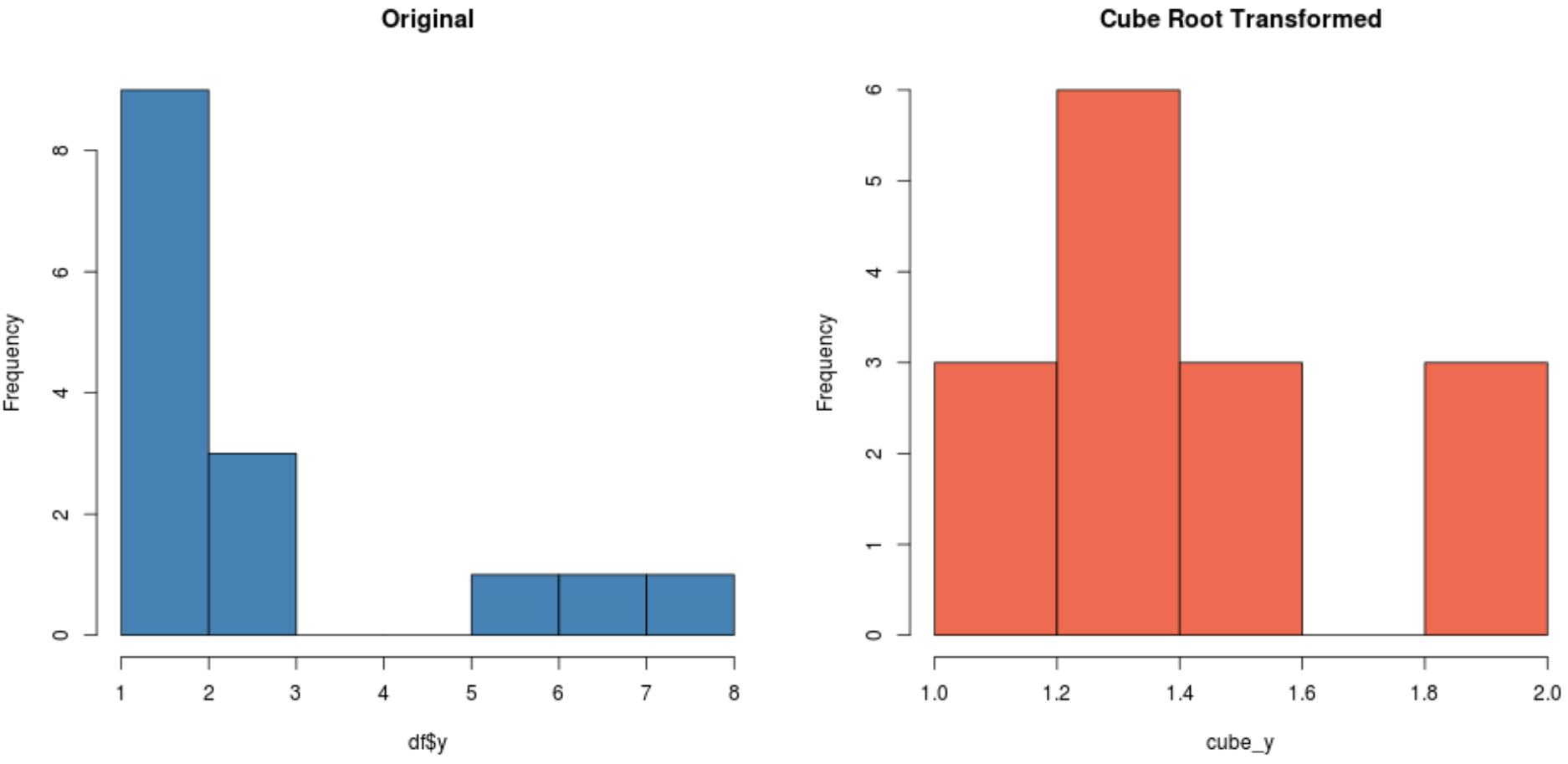
W zależności od zbioru danych jedna z tych transformacji może skutkować utworzeniem nowego zbioru danych o bardziej normalnym rozkładzie niż pozostałe.