Funkcja gęstości

Przez Benjamin Anderson 5 sierpnia, 2023 Prawdopodobieństwo 0 komentarzy

W tym artykule dowiesz się, czym jest funkcja gęstości, w jaki sposób oblicza się prawdopodobieństwo z funkcji gęstości oraz charakterystykę tej funkcji probabilistycznej. Dodatkowo będziesz mógł zobaczyć, jakie są różnice między funkcją gęstości a funkcją rozkładu.

Jaka jest funkcja gęstości?

Funkcja gęstości , zwana także funkcją gęstości prawdopodobieństwa , jest funkcją matematyczną opisującą prawdopodobieństwo, że ciągła zmienna losowa przyjmie określoną wartość.

Innymi słowy, funkcja gęstości powiązana ze zmienną matematycznie określa prawdopodobieństwo, że zmienna przyjmie wartość.

Załóżmy na przykład, że prawdopodobieństwo, że dorosła osoba jest wyższa niż 1,80 m w populacji wynosi 35%, wówczas funkcja gęstości wskaże prawdopodobieństwo 35% przy obliczaniu tego prawdopodobieństwa.

Czasami funkcja gęstości prawdopodobieństwa jest skracana jako PDF.

Oblicz prawdopodobieństwo za pomocą funkcji gęstości

Aby znaleźć prawdopodobieństwo, że zmienna ciągła przyjmie wartość z przedziału, należy obliczyć całkę funkcji gęstości związanej z tą zmienną pomiędzy granicami przedziału.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx$

Złoto

$f(x)$

jest funkcją gęstości ciągłej zmiennej losowej.

Innymi słowy, prawdopodobieństwo, że zmienna przyjmie wartość z przedziału, jest równe polu powierzchni pod funkcją gęstości w tym przedziale.

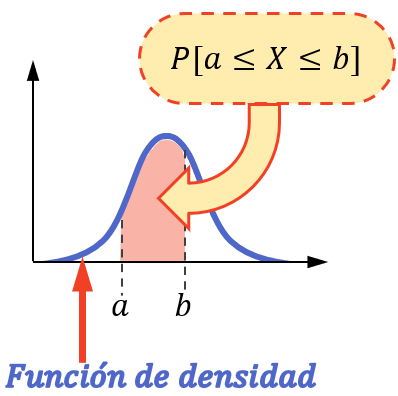
Należy zauważyć, że obliczenia prawdopodobieństwa można wykonać w ten sposób tylko wtedy, gdy zmienna statystyczna ma rozkład ciągły, taki jak rozkład normalny, rozkład wykładniczy, rozkład Poissona itp.

Własności funkcji gęstości

Funkcja gęstości ma następujące właściwości:

Wartość funkcji gęstości wynosi zero lub jest dodatnia dla dowolnej wartości x.

$f(x)\geq 0$

Dodatkowo maksymalna wartość funkcji gęstości jest równa 1.

$f(x)\leq 1$

W rzeczywistości całkowite pole pod wykresem funkcji gęstości jest zawsze równe 1 niezależnie od zmiennej, ponieważ odpowiada zbiorowi wszystkich prawdopodobieństw.

$\displaystyle \int_{-\infty}^{+\infty} f(x)dx=1$

Jak wyjaśniono w poprzedniej sekcji, prawdopodobieństwo, że zmienna ciągła przyjmie wartość z przedziału, oblicza się z całki funkcji gęstości w tym przedziale.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx=F(b)-F(a)$

Funkcja gęstości i funkcja rozkładu

W tej ostatniej sekcji zobaczymy, czym różni się funkcja gęstości od funkcji rozkładu, ponieważ są to dwa typy funkcji probabilistycznych, które są na ogół mylone.

Matematycznie funkcja dystrybucji jest równoważna całce funkcji gęstości , więc funkcja dystrybucji opisuje skumulowane prawdopodobieństwo zmiennej ciągłej.

Oznacza to, że obraz funkcji rozkładu dla dowolnej wartości jest równy prawdopodobieństwu, że zmienna przyjmie tę wartość lub niższą wartość.

Matematyczny związek między tymi dwoma typami funkcji jest zatem następujący:

$\displaystyle P[X\leq a]=\int_{-\infty}^a f(x)dx=F(a)$

Złoto

$f(x)$

jest funkcją gęstości i

$F(x)$

jest funkcją dystrybucji.

Zwróć uwagę, jak zmienia się graficzna reprezentacja funkcji gęstości w stosunku do jej funkcji rozkładu zmiennej, która ma rozkład normalny ze średnią 1 i odchyleniem standardowym 0,5:

różnica między funkcją rozkładu a funkcją gęstości

Aby dowiedzieć się więcej o funkcji dystrybucji, kliknij poniższy link:

➤ Patrz: funkcja dystrybucji

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej