Pełny kod Pythona użyty w tym samouczku można znaleźć tutaj .
Jak przeprowadzić regresję logistyczną w pythonie (krok po kroku)
Regresja logistyczna to metoda, której możemy użyć do dopasowania modelu regresji, gdy zmienna odpowiedzi jest binarna.
Regresja logistyczna wykorzystuje metodę zwaną estymacją największej wiarygodności w celu znalezienia równania w następującej postaci:
log[p(X) / ( 1 -p(X))] = β 0 + β 1 X 1 + β 2 X 2 + … + β p
Złoto:
- X j : j- ta zmienna predykcyjna
- β j : estymacja współczynnika dla j -tej zmiennej predykcyjnej
Wzór po prawej stronie równania przewiduje logarytm szansy , że zmienna odpowiedzi przyjmie wartość 1.
Zatem dopasowując model regresji logistycznej, możemy użyć poniższego równania do obliczenia prawdopodobieństwa, że dana obserwacja przyjmie wartość 1:
p(X) = e β 0 + β 1 X 1 + β 2 X 2 + … + β p
Następnie używamy pewnego progu prawdopodobieństwa, aby sklasyfikować obserwację jako 1 lub 0.
Na przykład możemy powiedzieć, że obserwacje z prawdopodobieństwem większym lub równym 0,5 zostaną sklasyfikowane jako „1”, a wszystkie inne obserwacje zostaną sklasyfikowane jako „0”.
W tym samouczku przedstawiono krok po kroku przykład wykonania regresji logistycznej w języku R.
Krok 1: Zaimportuj niezbędne pakiety
Najpierw zaimportujemy niezbędne pakiety, aby wykonać regresję logistyczną w Pythonie:
import pandas as pd import numpy as np from sklearn. model_selection import train_test_split from sklearn. linear_model import LogisticRegression from sklearn import metrics import matplotlib. pyplot as plt
Krok 2: Załaduj dane
W tym przykładzie użyjemy domyślnego zestawu danych z książki Wprowadzenie do uczenia się statystycznego . Możemy użyć następującego kodu, aby załadować i wyświetlić podsumowanie zbioru danych:
#import dataset from CSV file on Github url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv" data = pd. read_csv (url) #view first six rows of dataset data[0:6] default student balance income 0 0 0 729.526495 44361.625074 1 0 1 817.180407 12106.134700 2 0 0 1073.549164 31767.138947 3 0 0 529.250605 35704.493935 4 0 0 785.655883 38463.495879 5 0 1 919.588530 7491.558572 #find total observations in dataset len( data.index ) 10000
Ten zbiór danych zawiera następujące informacje na temat 10 000 osób:
- default: wskazuje, czy dana osoba nie wywiązała się ze zobowiązania, czy nie.
- student: wskazuje, czy dana osoba jest studentem, czy nie.
- saldo: Średnie saldo utrzymywane przez osobę.
- dochód: Dochód osoby fizycznej.
Wykorzystamy status studenta, stan konta bankowego i dochody, aby skonstruować model regresji logistycznej, który przewiduje prawdopodobieństwo niewypłacalności danej osoby.
Krok 3: Utwórz próbki szkoleniowe i testowe
Następnie podzielimy zbiór danych na zbiór uczący, na którym będziemy trenować model, oraz zbiór testowy, na którym będziemy testować model.
#define the predictor variables and the response variable X = data[[' student ',' balance ',' income ']] y = data[' default '] #split the dataset into training (70%) and testing (30%) sets X_train,X_test,y_train,y_test = train_test_split (X,y,test_size=0.3,random_state=0)
Krok 4: Dopasuj model regresji logistycznej
Następnie użyjemy funkcji LogisticRegression(), aby dopasować model regresji logistycznej do zbioru danych:
#instantiate the model log_regression = LogisticRegression() #fit the model using the training data log_regression. fit (X_train,y_train) #use model to make predictions on test data y_pred = log_regression. predict (X_test)
Krok 5: Diagnostyka modelu
Po dopasowaniu modelu regresji możemy następnie przeanalizować działanie naszego modelu na testowym zbiorze danych.
Najpierw utworzymy macierz zamieszania dla modelu:
cnf_matrix = metrics. confusion_matrix (y_test, y_pred)
cnf_matrix
array([[2886, 1],
[113,0]])
Z macierzy zamieszania widzimy, że:
- #Prawdziwie pozytywne przewidywania: 2886
- #Prawdziwie negatywne przewidywania: 0
- #Fałszywie pozytywne przewidywania: 113
- #Fałszywe negatywne przewidywania: 1
Możemy również uzyskać model dokładności, który informuje nas o procentowym przewidywaniu korekt dokonanym przez model:
print(" Accuracy: ", metrics.accuracy_score (y_test, y_pred))l
Accuracy: 0.962
To mówi nam, że model prawidłowo przewidział, czy dana osoba nie wywiąże się ze zobowiązań w 96,2% przypadków.
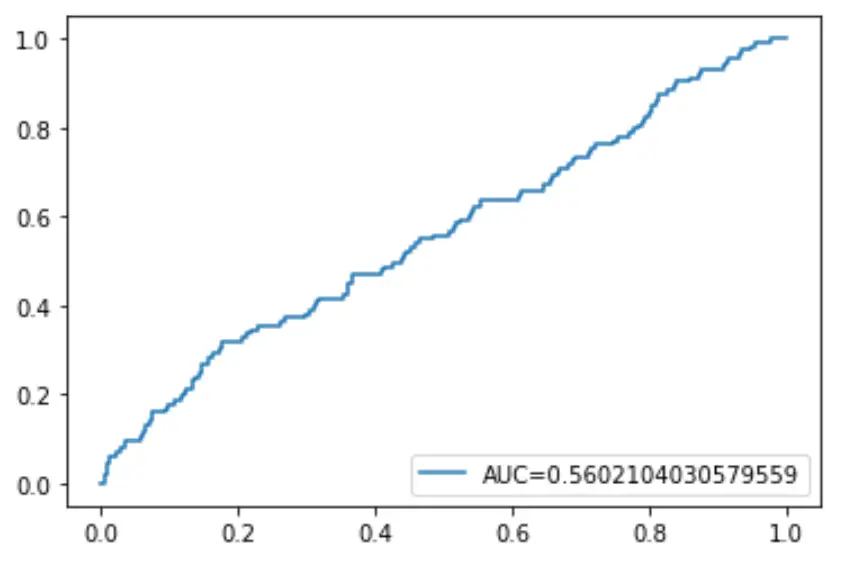
Na koniec możemy wykreślić krzywą charakterystyki działania odbiornika (ROC), która wyświetla procent prawdziwie pozytywnych wyników przewidywanych przez model, gdy próg prawdopodobieństwa przewidywania zostanie obniżony z 1 do 0.
Im wyższy AUC (obszar pod krzywą), tym dokładniej nasz model jest w stanie przewidzieć wyniki:
#define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)
#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. legend (loc=4)
plt. show ()