Średnia kwadratowa

Przez Benjamin Anderson 6 sierpnia, 2023 Statystyka 0 komentarzy

Tutaj wyjaśniamy, czym jest średnia kwadratowa i jak jest obliczana. Dodatkowo poznasz zalety i wady stosowania średniej oraz krok po kroku rozwiązane ćwiczenie. Na koniec będziesz mógł obliczyć średnią kwadratową dowolnego zestawu danych za pomocą kalkulatora znajdującego się na końcu artykułu.

Jaki jest średni kwadrat?

Średnia kwadratowa jest miarą centralności statystyki opisowej. Średnia kwadratowa jest równa pierwiastkowi kwadratowemu średniej arytmetycznej kwadratów danych.

Średnia kwadratowa jest również nazywana średnią kwadratową lub RMS .

Wzór na średnią kwadratową jest zatem następujący:

Średnia kwadratowa jest szczególnie przydatna, gdy zmienna statystyczna przyjmuje wartości dodatnie i ujemne, ponieważ podnosząc do kwadratu każdą część danych, wszystkie wartości stają się dodatnie. Dlatego do analizy zmiennych, w których ważny jest nie znak, ale jego wartość bezwzględna, wykorzystuje się średni kwadrat.

Na przykład średni kwadrat służy do badania błędów pomiaru, ponieważ w takich przypadkach nie sprawdzamy, czy błąd jest dodatni czy ujemny, ale raczej analizujemy wielkość błędu podczas pomiaru.

Dodatkowo kwadraty dużych liczb mają znacznie wyższe wartości niż kwadraty małych liczb, więc w środkowym kwadracie duże liczby są ważniejsze niż małe liczby.

Średnia kwadratowa to rodzaj średniej statystycznej wraz ze średnią arytmetyczną, średnią ważoną, średnią geometryczną i średnią harmoniczną.

Zalety i wady średniej kwadratowej

Średnia kwadratowa ma zalety i wady w porównaniu do innych typów średnich.

Główną zaletą średniej kwadratowej jest to, że pozwala ona uzyskać bardzo dobre przybliżenie średniej wartości zmiennej dyskretnej. Z drugiej strony dużą wadą średniej kwadratowej jest to, że jej obliczenie jest dość skomplikowane, ponieważ należy wykonać kilka operacji.

Natomiast średnia kwadratowa jest bardzo przydatna do analizy pomiarów błędów. Przywiązuje się również znacznie większą wagę do wysokich wartości, chociaż ta właściwość oznacza, że błędny pomiar znacząco zmieni wynik skuteczny.

Jak obliczyć średnią kwadratową

Aby obliczyć średnią kwadratową, należy wykonać następujące kroki:

Oblicz kwadrat każdych danych statystycznych.
Dodaj wszystkie kwadraty obliczone w poprzednim kroku.
Wynik podziel przez liczbę elementów danych w próbie.
Znajdź pierwiastek kwadratowy z poprzedniej wartości.
Otrzymany wynik jest średnią kwadratową próbki statystycznej.

👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć średnią kwadratową dowolnego zbioru danych.

Średni kwadratowy przykład

Kiedy już wiemy, jak obliczyć średnią kwadratową, jako przykład wyznaczymy średnią kwadratową zbioru danych.

Podczas zajęć w laboratorium uniwersyteckim profesor prosi swoich studentów o wykonanie eksperymentu z substancjami chemicznymi. Celem doświadczenia chemicznego jest otrzymanie roztworu o łącznej objętości 3 litrów. Grupy studenckie uzyskały następujące dane:

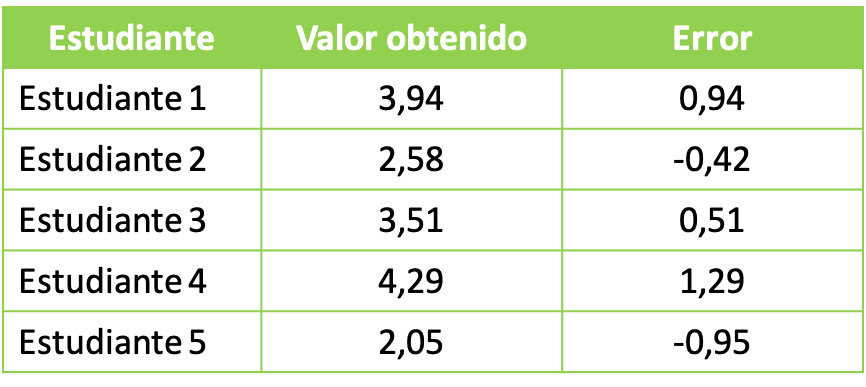
W celu zbadania uzyskanych danych statystycznych przystępujemy do obliczenia wartości średniej kwadratowej z błędem uzyskanym przez każdą grupę. Dlatego stosujemy wzór na średnią kwadratową:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

Podstawiamy dane do wzoru i obliczamy średnią kwadratową:

$\displaystyle RMS=\sqrt{\frac{0,94^2+(-0,42)^2+0,51^2+1,29^2+(-0,95)^2}{5}}=0,88$

Zatem średni błąd uzyskany w eksperymencie, zgodnie ze średnią kwadratową, wynosi 0,88 litra.

Średni kwadratowy kalkulator

Wprowadź dane z dowolnej próbki statystycznej do poniższego kalkulatora, aby obliczyć jej średnią kwadratową. Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej