Mle dla rozkładu poissona (krok po kroku)
Estymacja największej wiarygodności (MLE) to metoda, którą można zastosować do oszacowania parametrów danego rozkładu.
W tym samouczku wyjaśniono, jak obliczyć MLE dla parametru λ rozkładu Poissona .
Krok 1: Napisz plik PDF.
Najpierw napisz funkcję gęstości prawdopodobieństwa rozkładu Poissona:
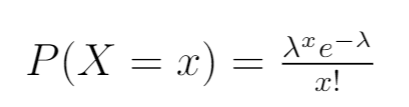
Krok 2: Napisz funkcję wiarygodności.
Następnie napisz funkcję wiarygodności. Jest to po prostu iloczyn pliku PDF dla zaobserwowanych wartości x 1 , …, x n .
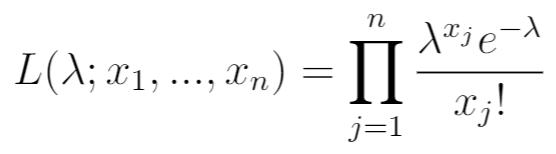
Krok 3: Zapisz funkcję wiarygodności logarytmu naturalnego.
Aby uprościć obliczenia, możemy napisać funkcję wiarygodności naturalnej:
Krok 4: Oblicz pochodną funkcji wiarygodności naturalnej względem λ.
Następnie możemy obliczyć pochodną funkcji wiarygodności naturalnej po parametrze λ:
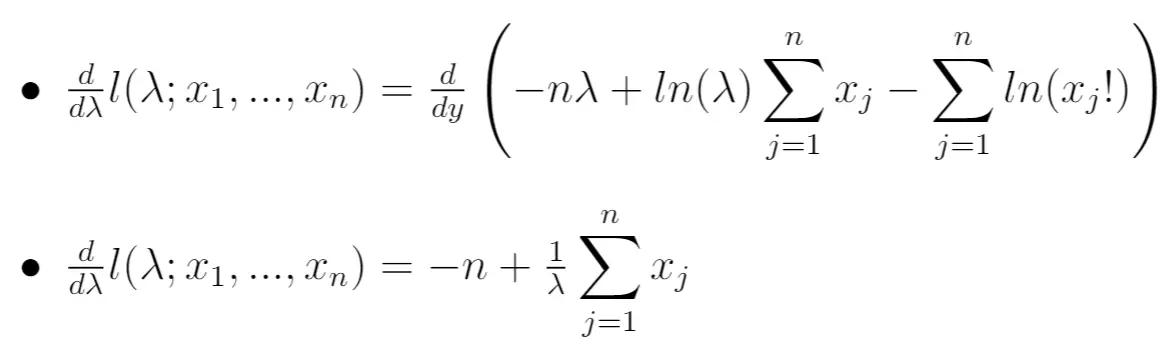
Krok 5: Ustaw pochodną na zero i oblicz λ.
Na koniec ustawiamy pochodną z poprzedniego kroku na zero i po prostu obliczamy λ:
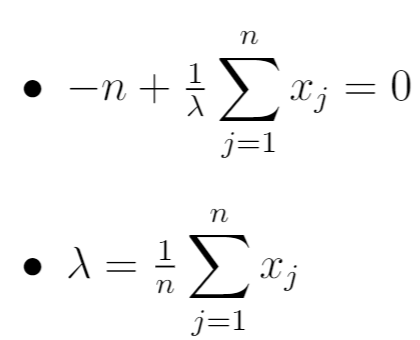
Zatem MLE okazuje się być:
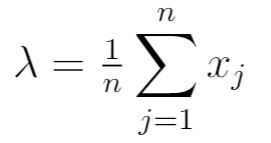
Jest to równoważne średniej próbki z n obserwacji w próbie.
Dodatkowe zasoby
Wprowadzenie do rozkładu Poissona
Kalkulator dystrybucji ryb
Jak korzystać z rozkładu Poissona w Excelu
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej