Wielokrotna regresja liniowa ręczna (krok po kroku)
Wielokrotna regresja liniowa to metoda, którą możemy zastosować do ilościowego określenia związku między dwiema lub większą liczbą zmiennych predykcyjnych a zmienną odpowiedzi .
W tym samouczku wyjaśniono, jak ręcznie wykonać wielokrotną regresję liniową.
Przykład: ręczna wielokrotna regresja liniowa
Załóżmy, że mamy następujący zestaw danych ze zmienną odpowiedzi y i dwiema zmiennymi predykcyjnymi x 1 i x 2 :
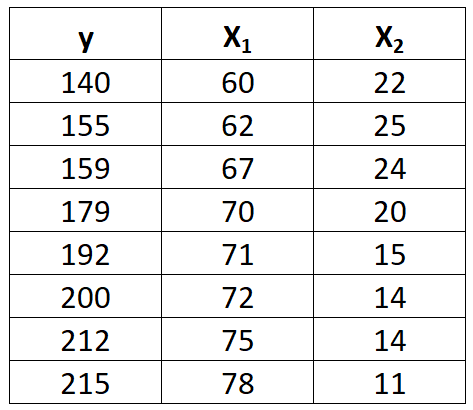
Wykonaj poniższe kroki, aby dopasować model regresji liniowej do tego zbioru danych.
Krok 1: Oblicz x 1 2 , x 2 2 , x 1 y, x 2 y i x 1 x 2 .
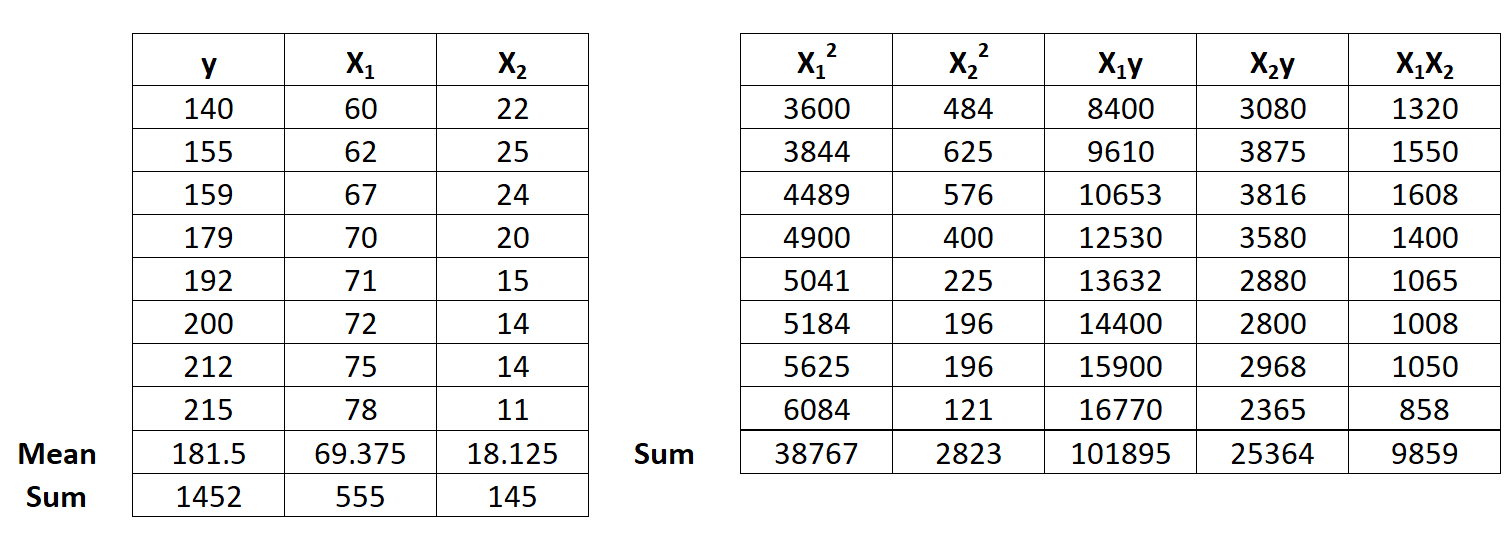
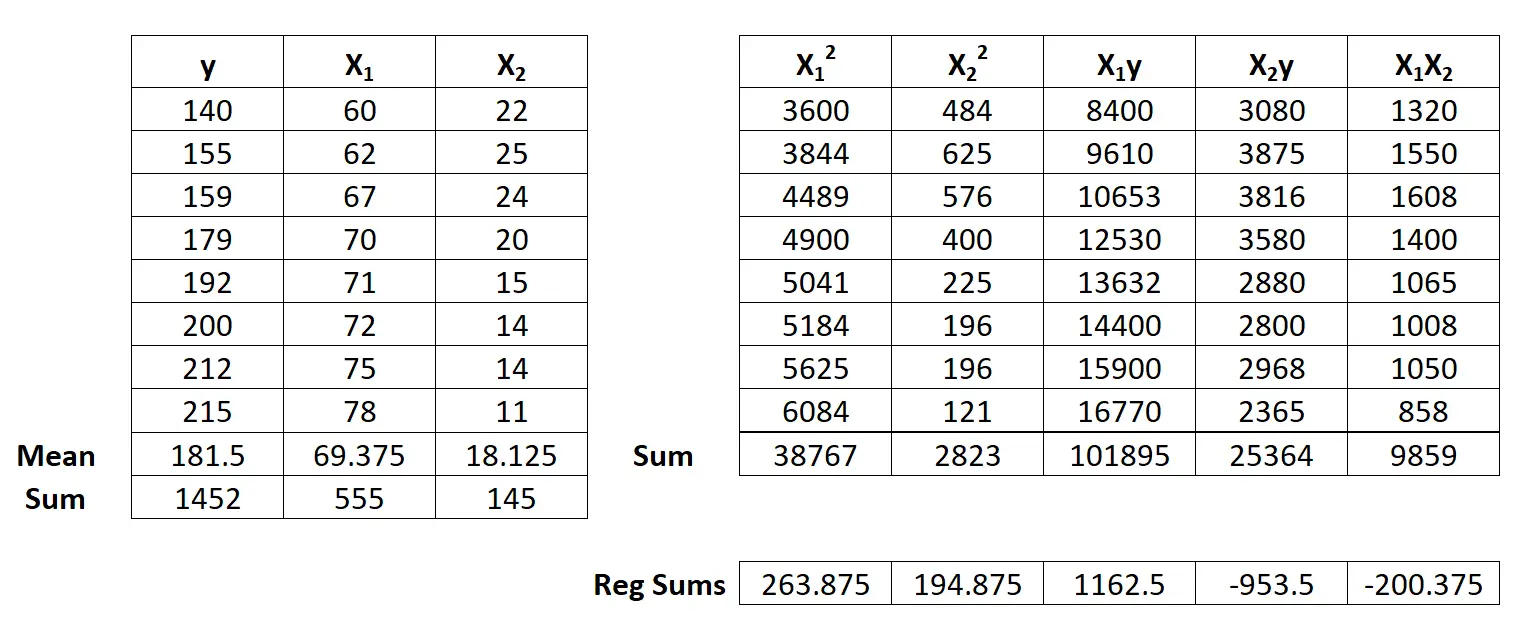
Krok 2: Oblicz sumy regresji.
Następnie wykonaj następujące obliczenia sumy regresji:
- Σx12 = ΣX12 – ( ΣX1 ) 2 / n = 38,767 – (555) 2 / 8 = 263,875
- Σx22 = ΣX22 – ( ΣX2 ) 2 / n = 2823 – (145) 2 / 8 = 194,875
- Σ x 1 y = Σ
- Σ x 2 y = Σ
- Σ x 1 x 2 = Σ
Krok 3: Oblicz b 0 , b 1 i b 2 .
Wzór na obliczenie b 1 to: [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Zatem b 1 = [(194,875)(1162,5) – (-200,375)(-953,5)] / [(263,875) (194,875) – (-200,375) 2 ] = 3,148
Wzór na obliczenie b 2 to: [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Zatem b 2 = [(263,875)(-953,5) – (-200,375)(1152,5)] / [(263,875) (194,875) – (-200,375) 2 ] = -1,656
Wzór na obliczenie b 0 jest następujący: y – b 1 X 1 – b 2 X 2
Zatem b 0 = 181,5 – 3,148(69,375) – (-1,656)(18,125) = -6,867
Krok 5: Umieść b 0 , b 1 i b 2 w oszacowanym równaniu regresji liniowej.
Oszacowane równanie regresji liniowej ma postać: ŷ = b 0 + b 1 *x 1 + b 2 *x 2
W naszym przykładzie jest to ŷ = -6,867 + 3,148x 1 – 1,656x 2
Jak interpretować równanie regresji wielokrotnej liniowej
Oto jak zinterpretować to oszacowane równanie regresji liniowej: ŷ = -6,867 + 3,148x 1 – 1,656x 2
b0 = -6,867 . Gdy obie zmienne predykcyjne są równe zero, średnia wartość y wynosi -6,867.
b1 = 3,148 . Wzrost x 1 o jedną jednostkę wiąże się ze wzrostem y średnio o 3,148 jednostki, przy założeniu, że x 2 pozostaje stałe.
b2 = -1,656 . Wzrost x 2 o jedną jednostkę wiąże się ze spadkiem y średnio o 1656 jednostek, przy założeniu, że x 1 pozostaje stałe.
Dodatkowe zasoby
Wprowadzenie do wielokrotnej regresji liniowej
Jak ręcznie wykonać prostą regresję liniową
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej