Jak obliczyć rozkłady próbkowania w r

Rozkład próbkowania to rozkład prawdopodobieństwa określonej statystyki oparty na wielu losowych próbach z jednej populacji.

W tym samouczku wyjaśniono, jak wykonać następujące czynności z rozkładami próbkowania w języku R:

• Wygeneruj rozkład próbkowania.
• Wizualizuj rozkład próbkowania.
• Oblicz średnią i odchylenie standardowe rozkładu próbkowania.
• Oblicz prawdopodobieństwa dotyczące rozkładu próby.

Wygeneruj rozkład próbkowania w R

Poniższy kod pokazuje, jak wygenerować rozkład próbkowania w R:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656

W tym przykładzie użyliśmy funkcji rnorm() do obliczenia średniej z 10 000 próbek, w których każda wielkość próbki wynosiła 20, i została wygenerowana z rozkładu normalnego ze średnią 5,3 i odchyleniem standardowym 9.

Widzimy, że pierwsza próbka miała średnią 5,283992, druga próbka miała średnią 6,304845 i tak dalej.

Wizualizuj rozkład próbkowania

Poniższy kod pokazuje, jak utworzyć prosty histogram do wizualizacji rozkładu próbkowania:

 #create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

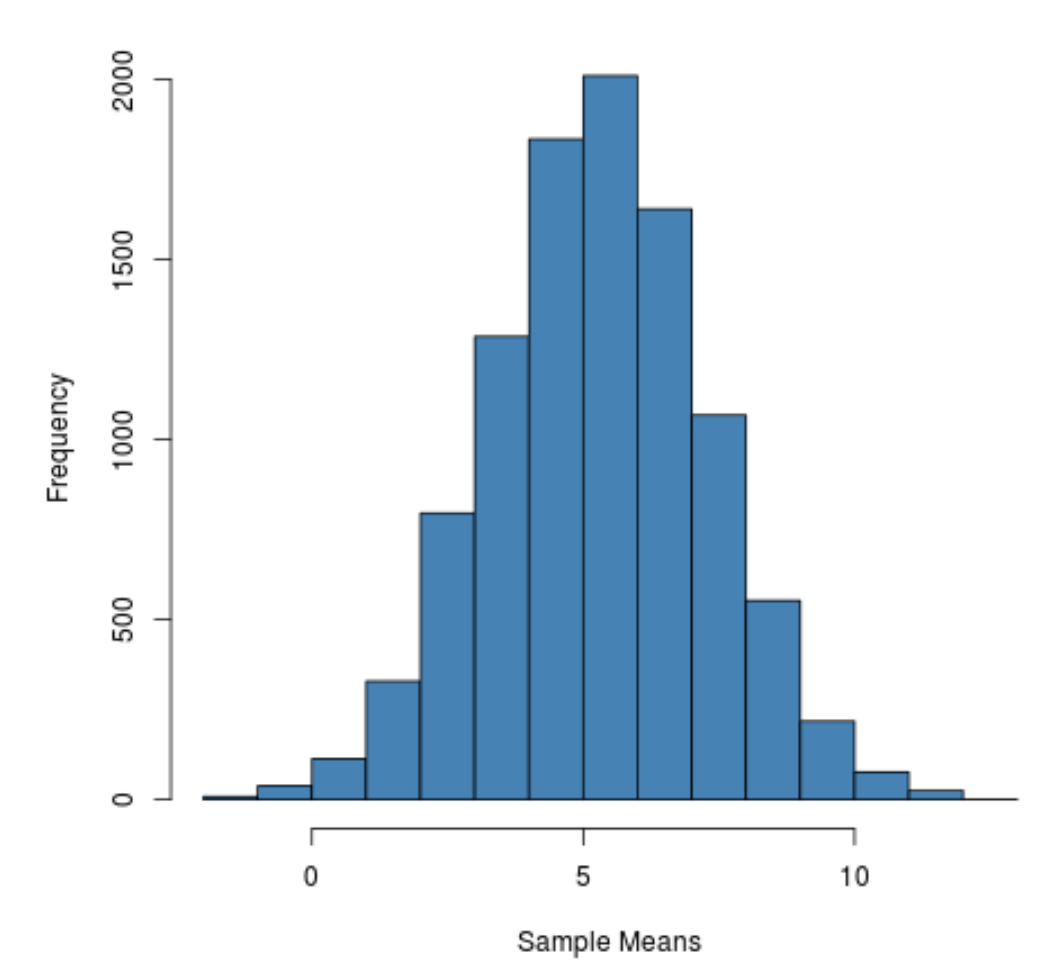
Można zauważyć, że rozkład próbkowania ma kształt dzwonu z pikiem w pobliżu wartości 5.

Jednak z ogonów rozkładu widać, że niektóre próbki miały średnie większe niż 10, a inne miały średnie mniejsze niż 0.

Znajdź średnią i odchylenie standardowe

Poniższy kod pokazuje, jak obliczyć średnią i odchylenie standardowe rozkładu próbkowania:

 #mean of sampling distribution
mean(sample_means)

[1] 5.287195

#standard deviation of sampling distribution
sd(sample_means)

[1] 2.00224

Teoretycznie średnia rozkładu próby powinna wynosić 5,3. Widzimy, że rzeczywista średnia z próbki w tym przykładzie wynosi 5,287195 , czyli blisko 5,3.

Teoretycznie odchylenie standardowe rozkładu próbkowania powinno być równe s/√n, czyli 9 / √20 = 2,012. Widzimy, że rzeczywiste odchylenie standardowe rozkładu próbkowania wynosi 2,00224 , co jest bliskie 2,012.

Oblicz prawdopodobieństwa

Poniższy kod pokazuje, jak obliczyć prawdopodobieństwo uzyskania określonej wartości średniej z próby, biorąc pod uwagę średnią populacji, odchylenie standardowe populacji i wielkość próby.

 #calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

W tym konkretnym przykładzie wyznaczamy prawdopodobieństwo, że średnia próbki jest mniejsza lub równa 6, przy założeniu, że średnia populacji wynosi 5,3, odchylenie standardowe populacji wynosi 9, a wielkość próby 20 wynosi 0,6417 .

Jest to bardzo zbliżone do prawdopodobieństwa obliczonego przez kalkulator rozkładu próbkowania :

Kompletny kod

Pełny kod R użyty w tym przykładzie pokazano poniżej:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

#mean of sampling distribution
mean(sample_means)

#standard deviation of sampling distribution
sd(sample_means)

#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

Dodatkowe zasoby

Wprowadzenie do rozkładów próbkowania
Kalkulator rozkładu próbkowania
Wprowadzenie do centralnego twierdzenia granicznego