Jak tworzyć losowe lasy w r (krok po kroku)

Kiedy związek między zbiorem zmiennych predykcyjnych a zmienną odpowiedzi jest bardzo złożony, często używamy metod nieliniowych do modelowania związku między nimi.

Jedną z takich metod jest zbudowanie drzewa decyzyjnego . Jednakże wadą stosowania pojedynczego drzewa decyzyjnego jest to, że charakteryzuje się ono dużą wariancją .

Oznacza to, że jeśli podzielimy zbiór danych na dwie połowy i zastosujemy drzewo decyzyjne do obu połówek, wyniki mogą być bardzo różne.

Jedną z metod, których możemy użyć do zmniejszenia wariancji pojedynczego drzewa decyzyjnego, jest zbudowanie losowego modelu lasu , który działa w następujący sposób:

1. Pobierz próbki bootstrapowe z oryginalnego zbioru danych.

2. Utwórz drzewo decyzyjne dla każdej próbki bootstrap.

• Podczas konstruowania drzewa za każdym razem, gdy rozważany jest podział, tylko losowa próbka m predyktorów jest uważana za kandydatów do podziału z pełnego zestawu p predyktorów. Generalnie wybieramy m równe √p .

3. Uśrednij przewidywania z każdego drzewa, aby otrzymać ostateczny model.

Okazuje się, że losowe lasy zwykle tworzą znacznie dokładniejsze modele niż pojedyncze drzewa decyzyjne, a nawet modele workowe .

W tym samouczku przedstawiono krok po kroku przykład tworzenia losowego modelu lasu dla zbioru danych w języku R.

Krok 1: Załaduj niezbędne pakiety

Najpierw załadujemy pakiety niezbędne dla tego przykładu. W tym prostym przykładzie potrzebujemy tylko jednego pakietu:

 library (randomForest)

Krok 2: Dostosuj model losowego lasu

W tym przykładzie użyjemy wbudowanego zbioru danych R o nazwie Air Quality , który zawiera pomiary jakości powietrza w Nowym Jorku w ciągu 153 poszczególnych dni.

 #view structure of air quality dataset
str(airquality)

'data.frame': 153 obs. of 6 variables:
 $ Ozone: int 41 36 12 18 NA 28 23 19 8 NA ...
 $Solar.R: int 190 118 149 313 NA NA 299 99 19 194 ...
 $ Wind: num 7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ...
 $ Temp: int 67 72 74 62 56 66 65 59 61 69 ...
 $Month: int 5 5 5 5 5 5 5 5 5 5 ...
 $Day: int 1 2 3 4 5 6 7 8 9 10 ...

#find number of rows with missing values
sum(! complete . cases (airquality))

[1] 42

Ten zbiór danych zawiera 42 wiersze z brakującymi wartościami. Dlatego przed dopasowaniem losowego modelu lasu uzupełnimy brakujące wartości w każdej kolumnie medianami kolumn:

 #replace NAs with column medians
for (i in 1: ncol (air quality)) {
  airquality[,i][ is . na (airquality[, i])] <- median (airquality[, i], na . rm = TRUE )
}

Powiązane: Jak przypisać brakujące wartości w R

Poniższy kod pokazuje, jak dopasować losowy model lasu w R przy użyciu funkcji randomForest() z pakietu randomForest .

 #make this example reproducible
set.seed(1)

#fit the random forest model
model <- randomForest(
  formula = Ozone ~ .,
  data = airquality
)

#display fitted model
model

Call:
 randomForest(formula = Ozone ~ ., data = airquality) 
               Type of random forest: regression
                     Number of trees: 500
No. of variables tried at each split: 1

          Mean of squared residuals: 327.0914
                    % Var explained: 61

#find number of trees that produce lowest test MSE
which.min(model$mse)

[1] 82

#find RMSE of best model
sqrt(model$mse[ which . min (model$mse)]) 

[1] 17.64392

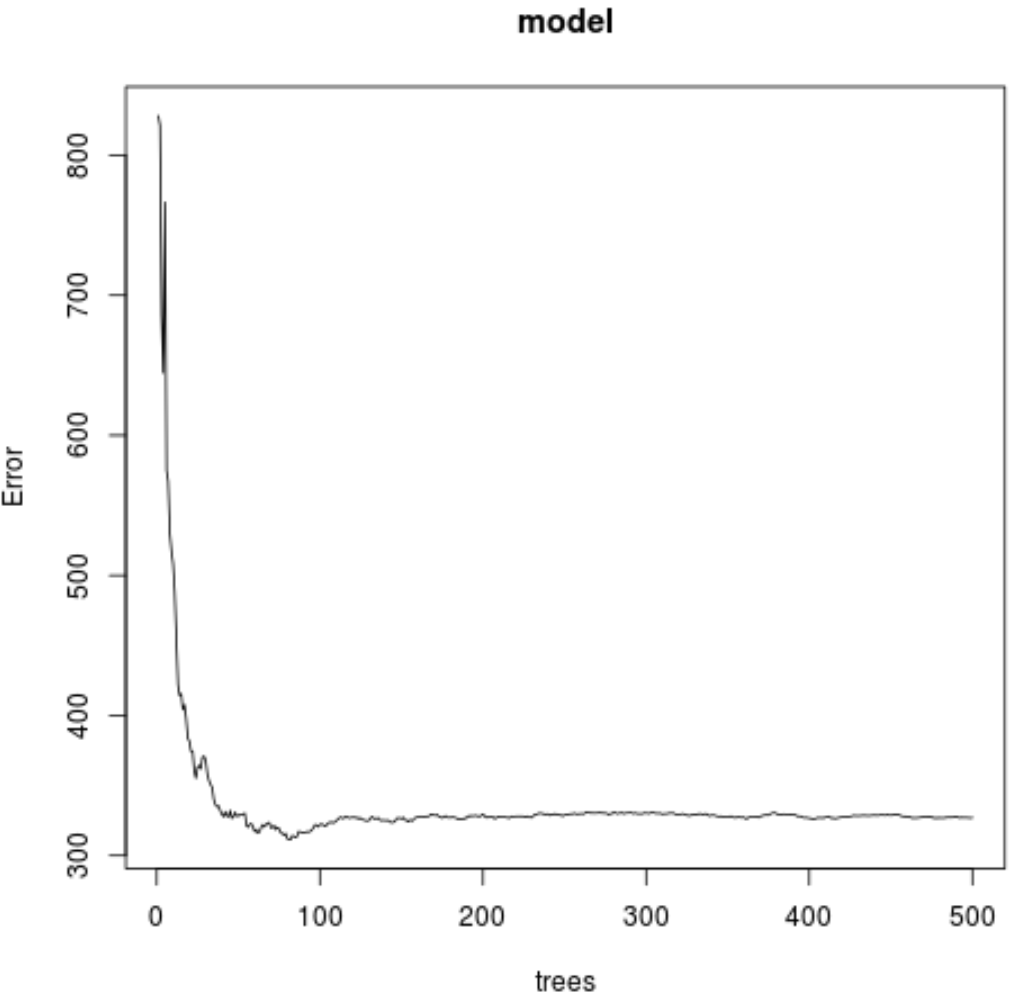
Z wyniku widać, że model, który wygenerował najniższy testowy błąd średniokwadratowy (MSE), wykorzystywał 82 drzewa.

Widzimy również, że średni błąd kwadratowy tego modelu wyniósł 17,64392 . Możemy to traktować jako średnią różnicę między przewidywaną wartością ozonu a rzeczywistą obserwowaną wartością.

Możemy również użyć poniższego kodu, aby utworzyć wykres testu MSE w oparciu o liczbę użytych drzew:

 #plot the MSE test by number of trees
plot(model)

Możemy także użyć funkcji varImpPlot() , aby utworzyć wykres przedstawiający ważność każdej zmiennej predykcyjnej w ostatecznym modelu:

 #produce variable importance plot
varImpPlot(model) 

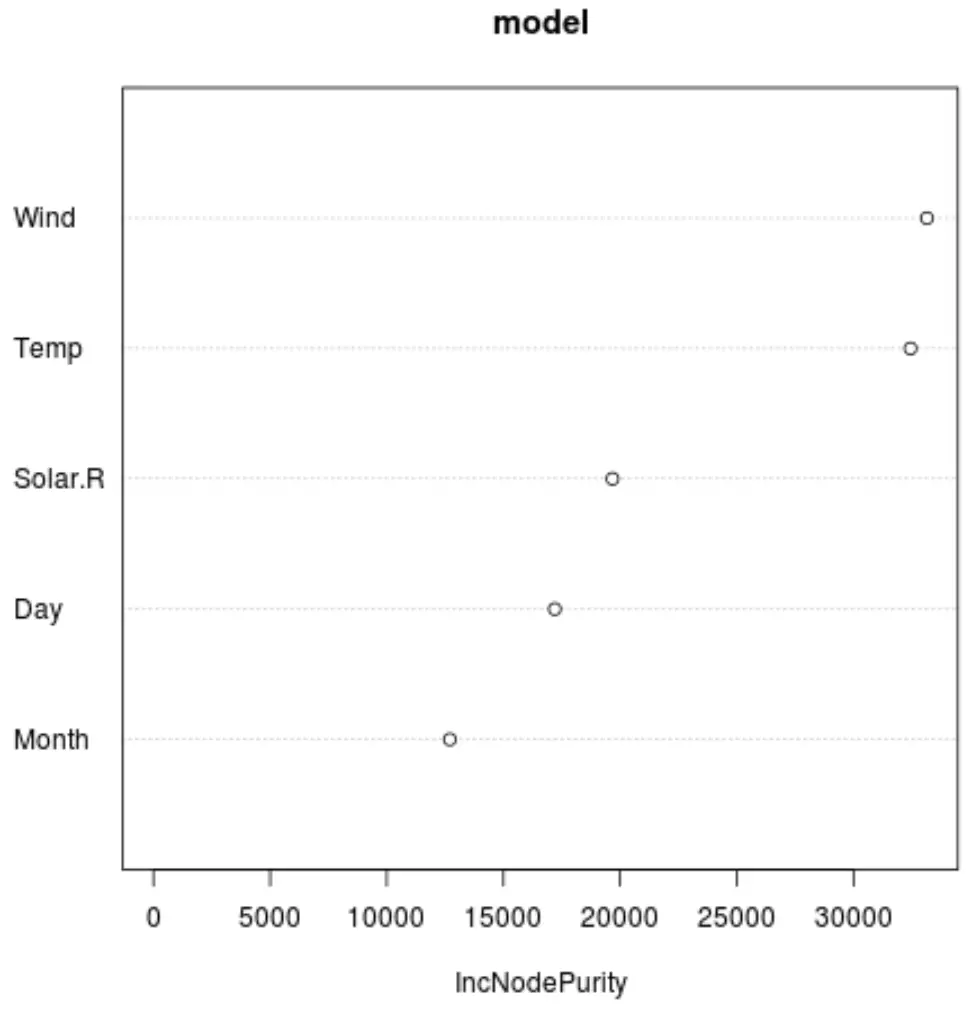
Oś x przedstawia średni wzrost czystości węzłów drzew regresji jako funkcję podziału na różne predyktory wyświetlane na osi y.

Z wykresu widzimy, że najważniejszą zmienną predykcyjną jest Wiatr , a tuż za nim znajduje się Temp .

Krok 3: Dopasuj model

Domyślnie funkcja randomForest() wykorzystuje 500 drzew i (łącznie predyktorów/3) losowo wybranych predyktorów jako potencjalnych kandydatów do każdego podziału. Możemy dostosować te parametry za pomocą funkcji tuneRF() .

Poniższy kod pokazuje, jak znaleźć optymalny model przy użyciu następujących specyfikacji:

• ntreeTry: Liczba drzew do zbudowania.
• mtryStart: początkowa liczba zmiennych predykcyjnych, które należy uwzględnić przy każdym podziale.
• stepFactor: Współczynnik zwiększany do momentu, aż szacowany błąd out-of-bag przestanie się poprawiać o określoną wartość.
• poprawić: wielkość, o jaką należy poprawić błąd wyjścia worka, aby w dalszym ciągu zwiększać współczynnik kroku.

 model_tuned <- tuneRF(
               x=airquality[,-1], #define predictor variables
               y=airquality$Ozone, #define response variable
               ntreeTry= 500 ,
               mtryStart= 4 , 
               stepFactor= 1.5 ,
               improve= 0.01 ,
               trace= FALSE #don't show real-time progress
               )

Ta funkcja generuje następujący wykres, który przedstawia liczbę predyktorów użytych przy każdym podziale podczas konstruowania drzew na osi x i szacowany błąd out-of-bag na osi y:

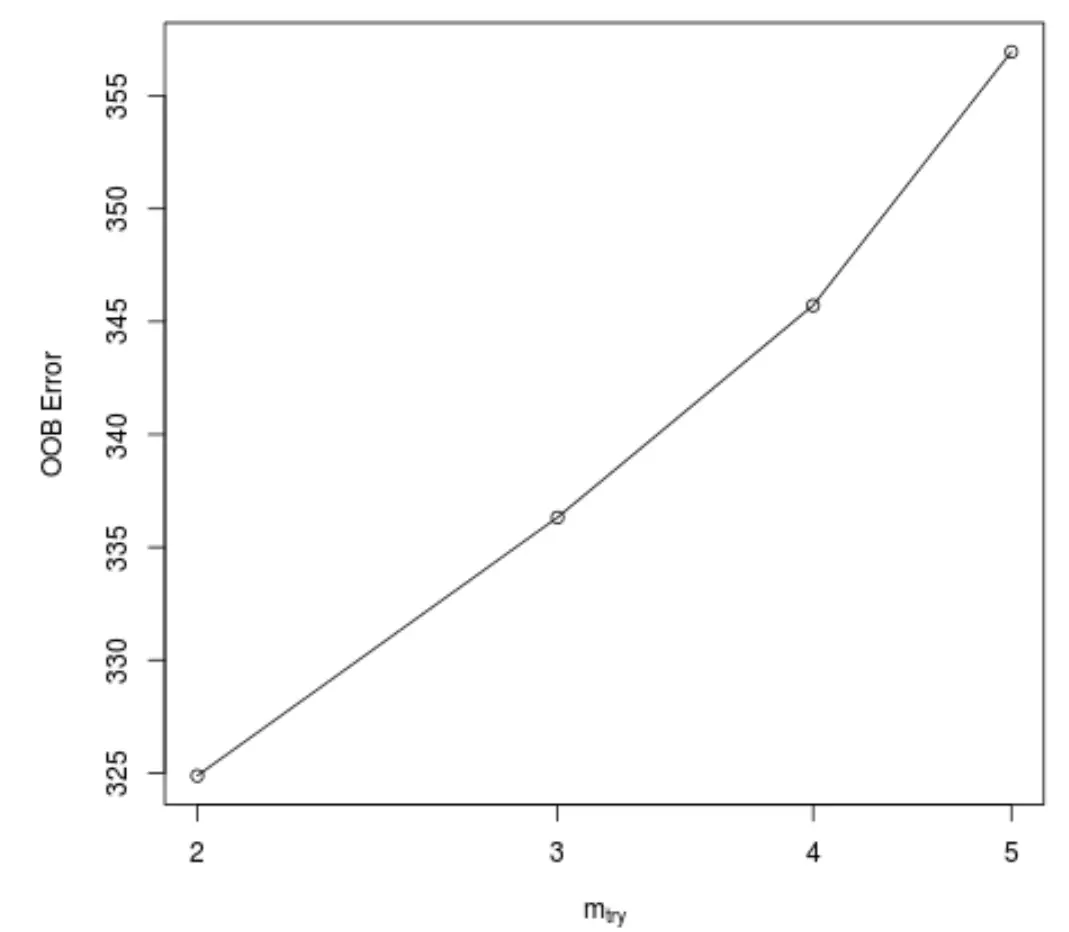
Widzimy, że najniższy błąd OOB uzyskuje się, stosując 2 losowo wybrane predyktory przy każdym podziale podczas budowania drzew.

W rzeczywistości odpowiada to ustawieniu domyślnemu (liczba predyktorów/3 = 6/3 = 2) używanemu przez początkową funkcję randomForest() .

Krok 4: Użyj ostatecznego modelu do przewidywania

Wreszcie możemy użyć skorygowanego modelu lasu losowego do przewidywania nowych obserwacji.

 #define new observation
new <- data.frame(Solar.R=150, Wind=8, Temp=70, Month=5, Day=5)

#use fitted bagged model to predict Ozone value of new observation
predict(model, newdata=new)

27.19442

Na podstawie wartości zmiennych predykcyjnych dopasowany losowy model lasu przewiduje, że w tym konkretnym dniu wartość ozonu wyniesie 27,19442 .

Pełny kod R użyty w tym przykładzie można znaleźć tutaj .