Analiza głównych składowych w r: przykład krok po kroku

Analiza głównych składowych, często w skrócie PCA, to technika uczenia maszynowego bez nadzoru , która ma na celu znalezienie głównych składowych – liniowych kombinacji oryginalnych predyktorów – które wyjaśniają dużą część zmienności w zbiorze danych.

Celem PCA jest wyjaśnienie większości zmienności w zbiorze danych przy użyciu mniejszej liczby zmiennych niż w oryginalnym zbiorze danych.

Dla danego zbioru danych zawierającego p zmiennych moglibyśmy zbadać wykresy rozrzutu każdej kombinacji par zmiennych, ale liczba wykresów rozrzutu może bardzo szybko stać się duża.

Dla predyktorów p istnieją chmury punktów p(p-1)/2.

Zatem dla zbioru danych z p = 15 predyktorów powstałoby 105 różnych wykresów rozrzutu!

Na szczęście PCA umożliwia znalezienie niskowymiarowej reprezentacji zbioru danych, która uwzględnia możliwie największą zmienność danych.

Jeśli uda nam się uchwycić większość zmienności w zaledwie dwóch wymiarach, moglibyśmy rzutować wszystkie obserwacje z oryginalnego zbioru danych na prosty wykres rozrzutu.

Sposób, w jaki znajdujemy główne komponenty, jest następujący:

_{Biorąc pod uwagę zbiór danych z predyktorami} p : _

• _{Z m = ΣΦjm _ _}
• Z ₁ to liniowa kombinacja predyktorów, która wychwytuje możliwie najwięcej wariancji.
• _Z2 jest następną liniową kombinacją predyktorów, która wychwytuje najwięcej wariancji, będąc ortogonalną (tzn. nieskorelowaną) z _Z1 .
• Z ₃ jest zatem następną liniową kombinacją predyktorów, która wychwytuje najwięcej wariancji, będąc ortogonalną do Z ₂ .
• I tak dalej.

W praktyce do obliczenia kombinacji liniowych oryginalnych predyktorów stosujemy następujące kroki:

1. Przeskaluj każdą ze zmiennych tak, aby miała średnią 0 i odchylenie standardowe 1.

2. Oblicz macierz kowariancji dla skalowanych zmiennych.

3. Oblicz wartości własne macierzy kowariancji.

Korzystając z algebry liniowej, możemy pokazać, że wektor własny odpowiadający największej wartości własnej jest pierwszą składową główną. Innymi słowy, ta konkretna kombinacja predyktorów wyjaśnia największą wariancję danych.

Wektor własny odpowiadający drugiej co do wielkości wartości własnej jest drugim głównym składnikiem i tak dalej.

W tym samouczku przedstawiono krok po kroku przykład wykonania tego procesu w języku R.

Krok 1: Załaduj dane

Najpierw załadujemy pakiet Tidyverse , który zawiera kilka przydatnych funkcji do wizualizacji i manipulowania danymi:

 library (tidyverse)

W tym przykładzie użyjemy zbioru danych USArrests wbudowanego w R, który zawiera liczbę aresztowań na 100 000 mieszkańców w każdym stanie USA w 1973 r. za morderstwo , napaść i gwałt .

Obejmuje także odsetek populacji każdego stanu zamieszkującej obszary miejskie, UrbanPop .

Poniższy kod pokazuje, jak załadować i wyświetlić pierwsze wiersze zbioru danych:

 #load data
data ("USArrests")

#view first six rows of data
head(USArrests)

           Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7

Krok 2: Oblicz główne składniki

Po załadowaniu danych możemy użyć wbudowanej funkcji prcomp() języka R do obliczenia głównych składników zbioru danych.

Pamiętaj, aby określić skalę = TRUE , aby przed obliczeniem głównych składników każda ze zmiennych w zbiorze danych została przeskalowana tak, aby miała średnią 0 i odchylenie standardowe 1.

Należy również zauważyć, że wektory własne w R domyślnie są skierowane w kierunku ujemnym, więc pomnożymy przez -1, aby odwrócić znaki.

 #calculate main components
results <- prcomp(USArrests, scale = TRUE )

#reverse the signs
results$rotation <- -1*results$rotation

#display main components
results$rotation

               PC1 PC2 PC3 PC4
Murder 0.5358995 -0.4181809 0.3412327 -0.64922780
Assault 0.5831836 -0.1879856 0.2681484 0.74340748
UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773
Rape 0.5434321 0.1673186 -0.8177779 -0.08902432

Widzimy, że pierwszy główny składnik (PC1) ma wysokie wartości dla morderstwa, napaści i gwałtu, co wskazuje, że ten główny składnik opisuje największe zróżnicowanie tych zmiennych.

Widzimy również, że drugi główny składnik (PC2) ma wysoką wartość dla UrbanPop, co wskazuje, że ten główny składnik kładzie nacisk na populację miejską.

Należy pamiętać, że wyniki głównych składników dla każdego stanu są przechowywane w plikuresults$x . Pomnożymy również te wyniki przez -1, aby odwrócić znaki:

 #reverse the signs of the scores
results$x <- -1*results$x

#display the first six scores
head(results$x)

                  PC1 PC2 PC3 PC4
Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581
Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454
Arizona 1.7454429 0.7384595 -0.05423025 0.826264240
Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554
California 2.4986128 1.5274267 -0.59254100 0.338559240
Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164

Krok 3: Wizualizuj wyniki za pomocą biplotu

Następnie możemy utworzyć biplot – wykres rzutujący każdą z obserwacji ze zbioru danych na wykres rozrzutu, który wykorzystuje pierwszą i drugą składową główną jako osie:

Należy pamiętać, że skala = 0 gwarantuje, że strzałki na wykresie będą skalowane w celu przedstawienia obciążeń.

 biplot(results, scale = 0 )

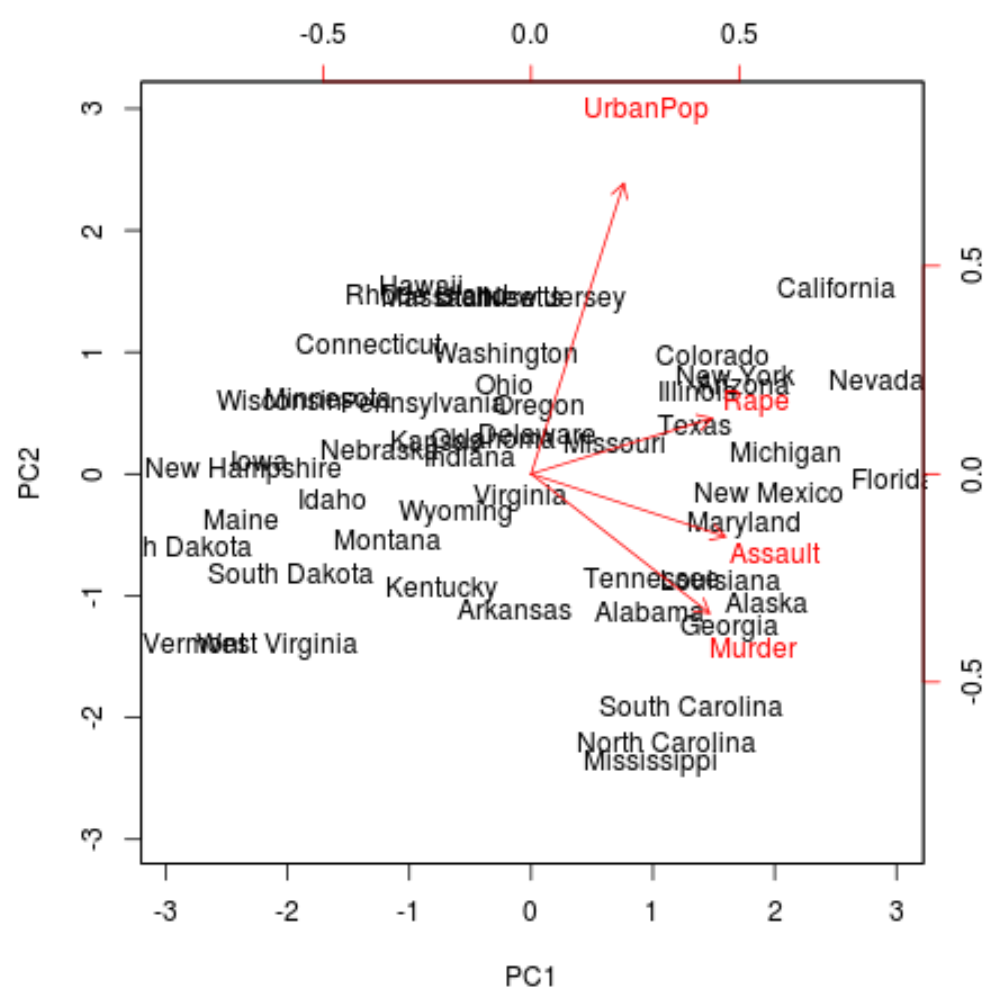
Na wykresie widzimy każdy z 50 stanów przedstawionych w prostej dwuwymiarowej przestrzeni.

Stany znajdujące się blisko siebie na wykresie mają podobne wzorce danych w odniesieniu do zmiennych w oryginalnym zbiorze danych.

Widzimy również, że niektóre stany są silniej powiązane z określonymi przestępstwami niż inne. Na przykład Georgia jest stanem położonym najbliżej zmiennej „Morderstwo” na wykresie.

Jeśli spojrzymy na stany o najwyższym wskaźniku morderstw w oryginalnym zbiorze danych, zobaczymy, że Gruzja faktycznie znajduje się na szczycie listy:

 #display states with highest murder rates in original dataset
head(USArrests[ order (-USArrests$Murder),])

               Murder Assault UrbanPop Rape
Georgia 17.4 211 60 25.8
Mississippi 16.1 259 44 17.1
Florida 15.4 335 80 31.9
Louisiana 15.4 249 66 22.2
South Carolina 14.4 279 48 22.5
Alabama 13.2 236 58 21.2

Krok 4: Znajdź wariancję wyjaśnioną przez każdy główny składnik

Możemy użyć następującego kodu, aby obliczyć całkowitą wariancję oryginalnego zbioru danych wyjaśnioną przez każdy główny składnik:

 #calculate total variance explained by each principal component
results$sdev^2 / sum (results$sdev^2)

[1] 0.62006039 0.24744129 0.08914080 0.04335752

Na podstawie wyników możemy zaobserwować, co następuje:

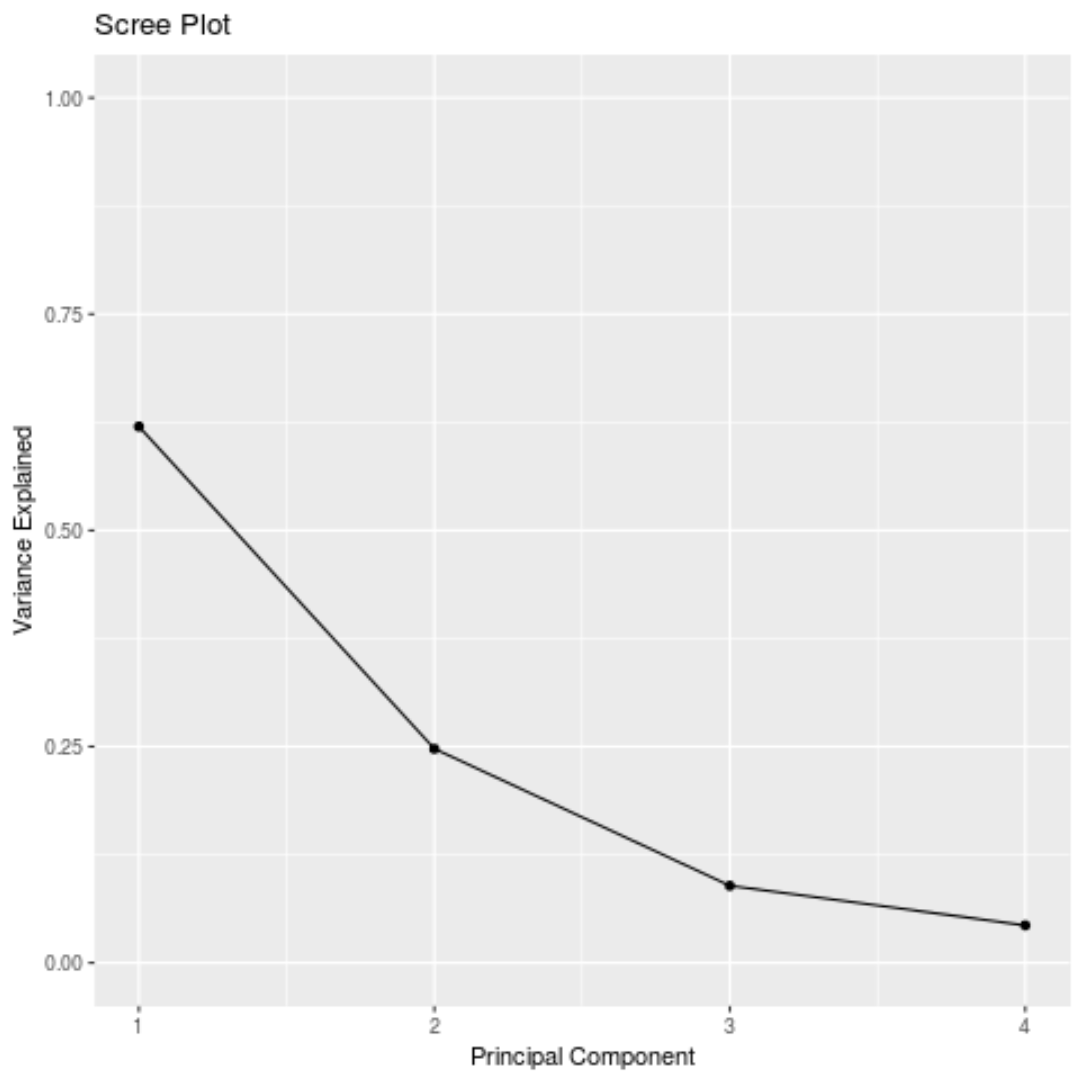
• Pierwszy główny składnik wyjaśnia 62% całkowitej wariancji w zbiorze danych.
• Drugi główny składnik wyjaśnia 24,7% całkowitej wariancji w zbiorze danych.
• Trzeci główny składnik wyjaśnia 8,9% całkowitej wariancji w zbiorze danych.
• Czwarty główny składnik wyjaśnia 4,3% całkowitej wariancji w zbiorze danych.

Zatem pierwsze dwa główne składniki wyjaśniają większość całkowitej wariancji danych.

To dobry znak, ponieważ w poprzednim biplot rzutowano każdą obserwację z oryginalnych danych na wykres rozrzutu, który uwzględniał tylko dwa pierwsze główne składniki.

Dlatego uzasadnione jest zbadanie wzorców na biplocie w celu zidentyfikowania stanów, które są do siebie podobne.

Możemy również utworzyć wykres osypiska – wykres przedstawiający całkowitą wariancję wyjaśnioną przez każdy główny składnik – w celu wizualizacji wyników PCA:

 #calculate total variance explained by each principal component
var_explained = results$sdev^2 / sum (results$sdev^2)

#create scree plot
qplot(c(1:4), var_explained) + 
  geom_line() + 
  xlab(" Principal Component ") + 
  ylab(" Variance Explained ") +
  ggtitle(" Scree Plot ") +
  ylim(0, 1) 

Analiza głównych składowych w praktyce

W praktyce PCA stosuje się najczęściej z dwóch powodów:

1. Eksploracyjna analiza danych – PCA używamy, gdy po raz pierwszy eksplorujemy zbiór danych i chcemy zrozumieć, które obserwacje w danych są do siebie najbardziej podobne.

2. Regresja głównych składowych – możemy również użyć PCA do obliczenia głównych składowych, które można następnie wykorzystać w regresji głównych składowych . Ten typ regresji jest często stosowany, gdy istnieje wieloliniowość między predyktorami w zbiorze danych.

Pełny kod R użyty w tym samouczku można znaleźć tutaj .