K-medoids w r: przykład krok po kroku

Grupowanie to technika uczenia maszynowego, która próbuje znaleźć grupy lub skupienia obserwacji w zbiorze danych.

Celem jest znalezienie takich skupień, w których obserwacje w każdym klastrze będą do siebie dość podobne, podczas gdy obserwacje w różnych skupieniach znacznie się od siebie różnią.

Klastrowanie jest formą uczenia się bez nadzoru , ponieważ po prostu staramy się znaleźć strukturę w zbiorze danych, zamiast przewidywać wartość zmiennej odpowiedzi .

Klastrowanie jest często stosowane w marketingu, gdy firmy mają dostęp do informacji takich jak:

• Przychód domowy
• Wielkość gospodarstwa domowego
• Zawód głowy gospodarstwa domowego
• Odległość do najbliższego obszaru miejskiego

Jeżeli takie informacje są dostępne, można zastosować grupowanie w celu zidentyfikowania gospodarstw domowych, które są podobne i które mogą z większym prawdopodobieństwem zakupić określone produkty lub lepiej reagować na określony rodzaj reklamy.

Jedną z najpowszechniejszych form grupowania jest grupowanie k-średnich .

Niestety na tę metodę mogą wpływać wartości odstające, dlatego często stosowaną alternatywą jest grupowanie k-medoidów .

Co to jest klastrowanie K-Medoids?

Grupowanie K-medoidów to technika, w której każdą obserwację ze zbioru danych umieszczamy w jednym z K klastrów.

Ostatecznym celem jest utworzenie K klastrów, w których obserwacje w każdym klastrze są do siebie dość podobne, podczas gdy obserwacje w różnych klastrach znacznie się od siebie różnią.

W praktyce do przeprowadzenia grupowania K-średnich stosujemy następujące kroki:

1. Wybierz wartość K.

• Najpierw musimy zdecydować, ile skupień chcemy zidentyfikować w danych. Często wystarczy po prostu przetestować kilka różnych wartości K i przeanalizować wyniki, aby zobaczyć, która liczba skupień wydaje się mieć największy sens dla danego problemu.

2. Losowo przypisz każdą obserwację do skupienia początkowego, od 1 do K.

3. Wykonuj poniższą procedurę, aż przypisania klastrów przestaną się zmieniać.

• Dla każdej z gromad K oblicz środek ciężkości gromady. Jest to wektor p median cech dla obserwacji k- tego skupienia.
• Przypisz każdą obserwację do klastra o najbliższym centroidzie. Tutaj najbliżej definiuje się odległość euklidesową .

Uwaga techniczna:

Ponieważ k-medoids oblicza centroidy klastrów przy użyciu median, a nie średnich, jest on zwykle bardziej odporny na wartości odstające niż k-średnie.

W praktyce, jeśli w zbiorze danych nie ma skrajnych wartości odstających, k-średnie i k-medoidy dadzą podobne wyniki.

Klaster K-Medoids w R

Poniższy samouczek zawiera przykład krok po kroku wykonywania grupowania k-medoids w języku R.

Krok 1: Załaduj niezbędne pakiety

Najpierw załadujemy dwa pakiety zawierające kilka przydatnych funkcji do grupowania k-medoids w R.

 library (factoextra)
library (cluster)

Krok 2: Załaduj i przygotuj dane

W tym przykładzie użyjemy zbioru danych USArrests wbudowanego w R, który zawiera liczbę aresztowań na 100 000 mieszkańców w każdym stanie USA w 1973 r. za morderstwo , napaść i gwałt , a także procent populacji każdego stanu mieszkającej w obszarach miejskich obszary. , UrbanPop .

Poniższy kod pokazuje, jak wykonać następujące czynności:

• Załaduj zbiór danych USArrests
• Usuń wszystkie wiersze z brakującymi wartościami
• Skaluj każdą zmienną w zbiorze danych tak, aby miała średnią 0 i odchylenie standardowe 1

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

Krok 3: Znajdź optymalną liczbę klastrów

Aby wykonać grupowanie k-medoid w R, możemy użyć funkcji pam() , która oznacza „partycjonowanie wokół median” i wykorzystuje następującą składnię:

pam(dane, k, metryka = „euklidesowy”, stojak = FAŁSZ)

Złoto:

• dane: nazwa zbioru danych.
• k: liczba klastrów.
• metryka: metryka używana do obliczania odległości. Wartość domyślna to Euclidean , ale możesz także określić Manhattan .
• stand: Określa, czy normalizować każdą zmienną w zbiorze danych. Wartość domyślna to fałsz.

Ponieważ nie wiemy z góry, jaka liczba skupień jest optymalna, utworzymy dwa różne wykresy, które pomogą nam podjąć decyzję:

1. Liczba skupień w stosunku do sumy kwadratów

Najpierw użyjemy funkcji fviz_nbclust() , aby utworzyć wykres liczby skupień w funkcji sumy kwadratów:

 fviz_nbclust(df, pam, method = “ wss ”) 

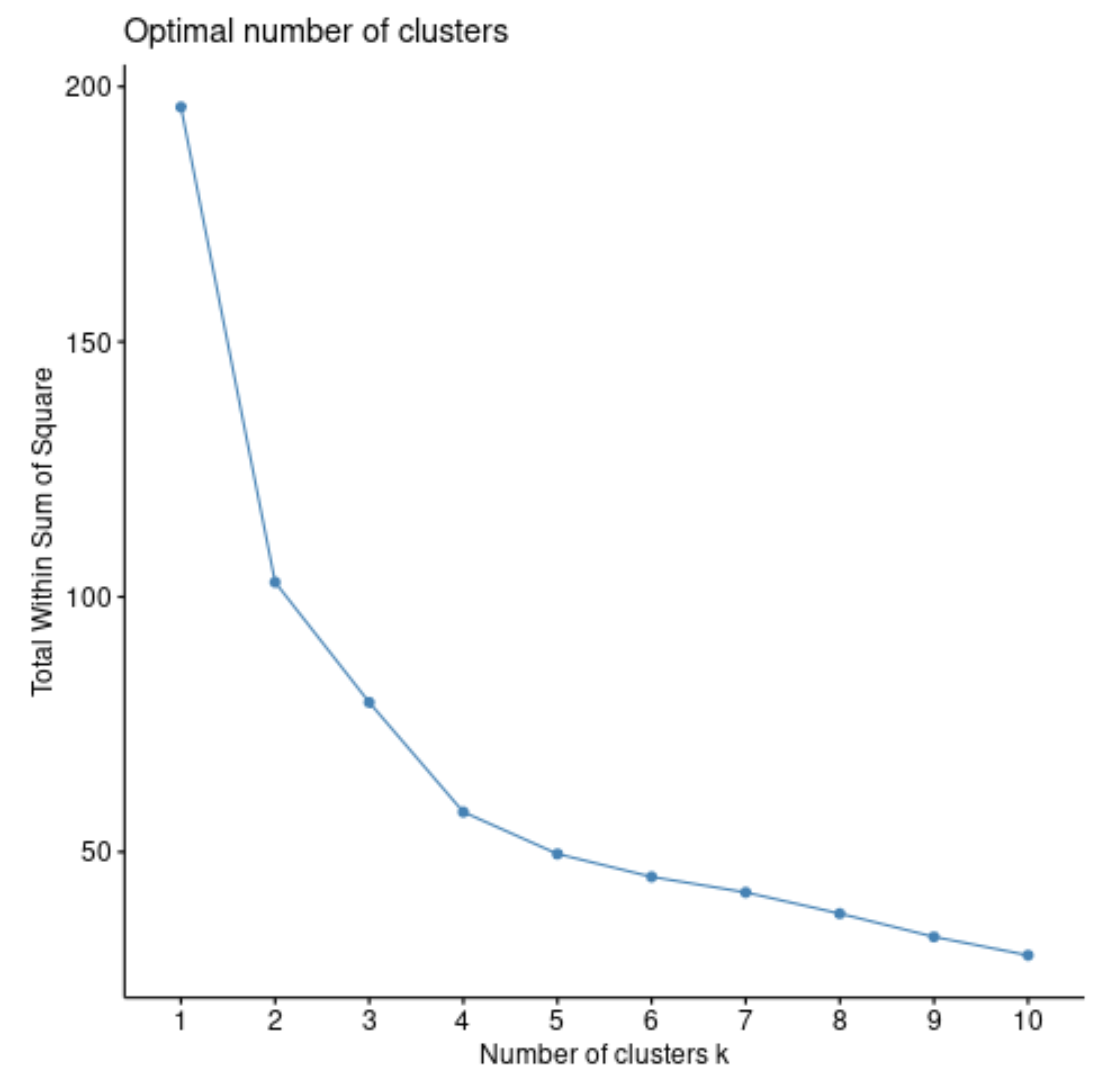
Suma kwadratów na ogół zawsze będzie rosła wraz ze zwiększaniem liczby klastrów. Kiedy więc tworzymy tego typu wykres, szukamy „kolana”, w którym suma kwadratów zaczyna się „zaginać” lub wyrównywać.

Punkt krzywizny wykresu generalnie odpowiada optymalnej liczbie skupień. Powyżej tej wartości prawdopodobne jest wystąpienie nadmiernego dopasowania .

W przypadku tego wykresu wydaje się, że przy k = 4 skupiskach występuje niewielkie załamanie lub „zagięcie”.

2. Liczba klastrów a statystyki luk

Innym sposobem określenia optymalnej liczby skupień jest użycie metryki zwanej statystyką odchyleń , która porównuje całkowitą zmienność wewnątrz skupień dla różnych wartości k z ich wartościami oczekiwanymi dla rozkładu bez grupowania.

Możemy obliczyć statystykę luk dla każdej liczby klastrów za pomocą funkcji clusGap() z pakietu klastrów , a także wykres klastrów w funkcji statystyki luk za pomocą funkcji fviz_gap_stat() :

 #calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = pam,
                    K.max = 10, #max clusters to consider
                    B = 50) #total bootstrapped iterations

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat) 

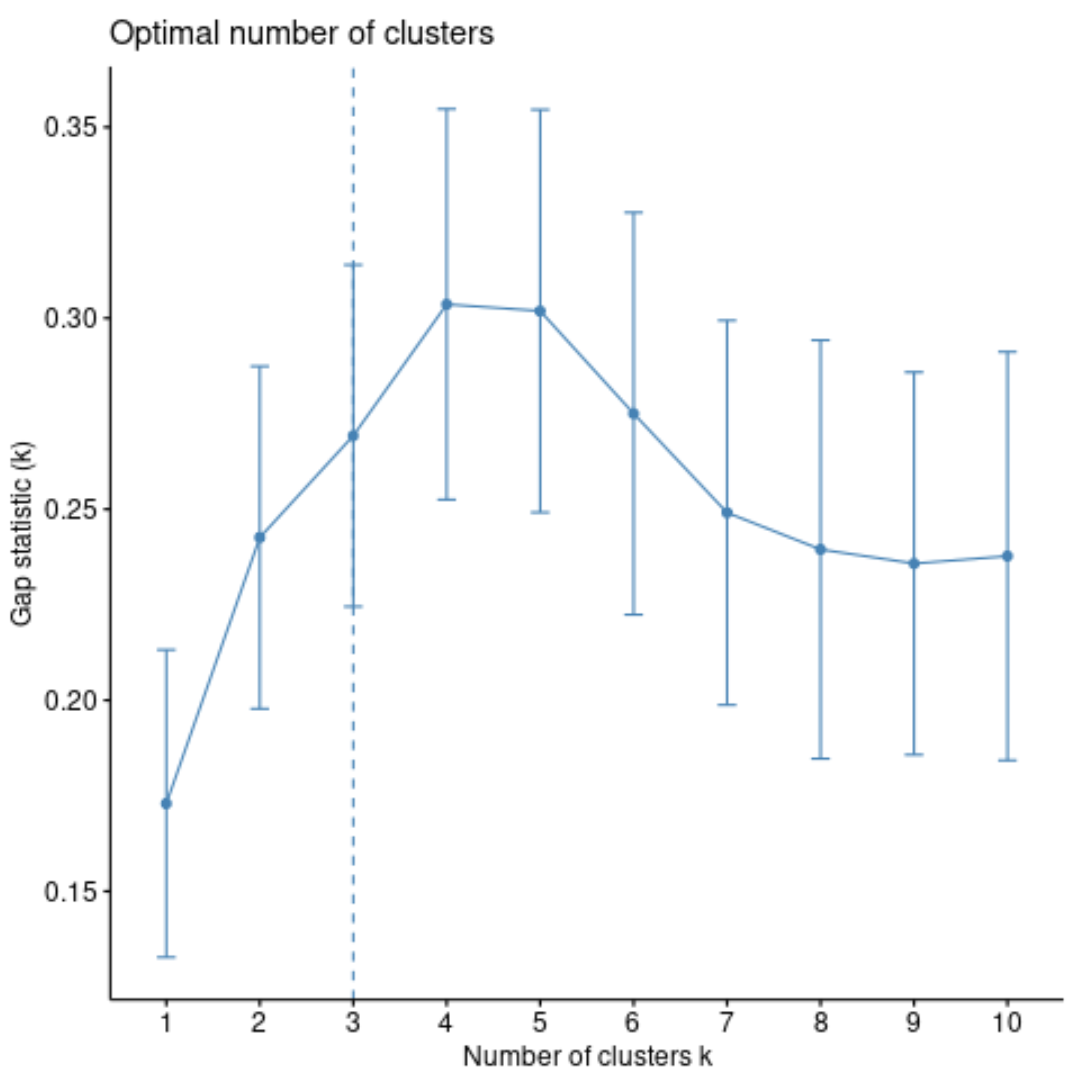
Z wykresu widać, że statystyka luki jest najwyższa przy k = 4 skupień, co odpowiada zastosowanej wcześniej metodzie łokcia.

Krok 4: Wykonaj grupowanie K-Medoids za pomocą Optimal K

Na koniec możemy wykonać grupowanie k-medoidów na zbiorze danych, używając optymalnej wartości k z 4:

 #make this example reproducible
set.seed(1)

#perform k-medoids clustering with k = 4 clusters
kmed <- pam(df, k = 4)

#view results
kmed

              ID Murder Assault UrbanPop Rape
Alabama 1 1.2425641 0.7828393 -0.5209066 -0.003416473
Michigan 22 0.9900104 1.0108275 0.5844655 1.480613993
Oklahoma 36 -0.2727580 -0.2371077 0.1699510 -0.131534211
New Hampshire 29 -1.3059321 -1.3650491 -0.6590781 -1.252564419
Vector clustering:
       Alabama Alaska Arizona Arkansas California 
             1 2 2 1 2 
      Colorado Connecticut Delaware Florida Georgia 
             2 3 3 2 1 
        Hawaii Idaho Illinois Indiana Iowa 
             3 4 2 3 4 
        Kansas Kentucky Louisiana Maine Maryland 
             3 3 1 4 2 
 Massachusetts Michigan Minnesota Mississippi Missouri 
             3 2 4 1 3 
       Montana Nebraska Nevada New Hampshire New Jersey 
             3 3 2 4 3 
    New Mexico New York North Carolina North Dakota Ohio 
             2 2 1 4 3 
      Oklahoma Oregon Pennsylvania Rhode Island South Carolina 
             3 3 3 3 1 
  South Dakota Tennessee Texas Utah Vermont 
             4 1 2 3 4 
      Virginia Washington West Virginia Wisconsin Wyoming 
             3 3 4 4 3 
Objective function:
   build swap 
1.035116 1.027102 

Available components:
 [1] "medoids" "id.med" "clustering" "objective" "isolation" 
 [6] "clusinfo" "silinfo" "diss" "call" "data"          

Należy zauważyć, że wszystkie cztery centroidy klastrów są rzeczywistymi obserwacjami w zbiorze danych. W górnej części wyniku widzimy, że cztery centroidy znajdują się w następujących stanach:

• Alabama
• Michigan
• Oklahoma
• New Hampshire

Możemy wizualizować skupienia na wykresie punktowym, który wyświetla pierwsze dwie główne składowe na osiach, używając funkcji fivz_cluster() :

 #plot results of final k-medoids model
fviz_cluster(kmed, data = df)

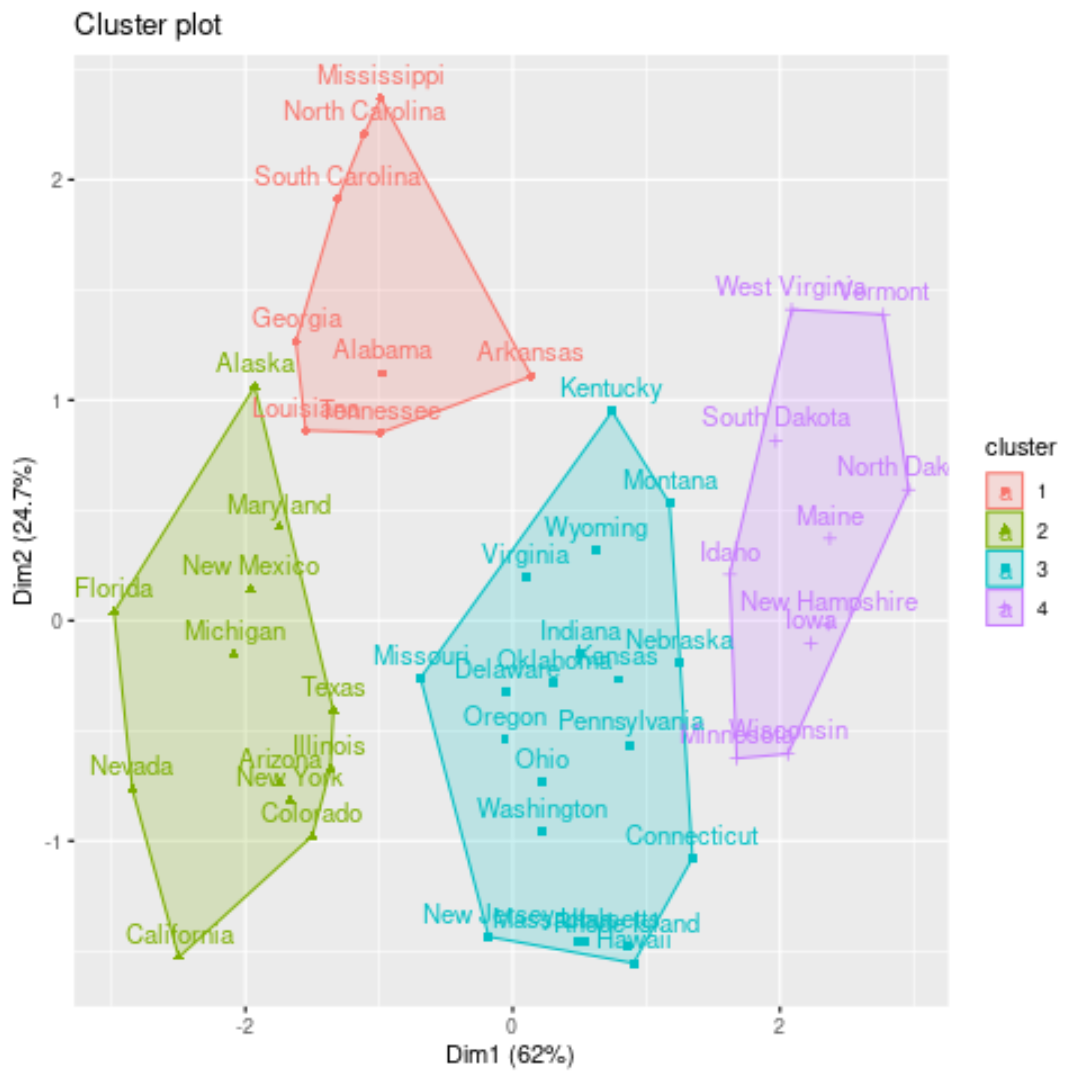
Możemy również dodać przypisania klastrów każdego stanu do oryginalnego zbioru danych:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = kmed$cluster)

#view final data
head(final_data)

           Murder Assault UrbanPop Rape cluster
Alabama 13.2 236 58 21.2 1
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 1
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Pełny kod R użyty w tym przykładzie znajdziesz tutaj .