Co to jest ograniczenie zakresu?

Często w statystyce staramy się mierzyć korelację między dwiema zmiennymi. Pomaga nam to zrozumieć następujące kwestie:

• Kierunek zależności pomiędzy dwiema zmiennymi. Czy w miarę wzrostu jednej zmiennej druga zmienna ma tendencję do zwiększania się czy zmniejszania?
• Siła związku pomiędzy dwiema zmiennymi. O ile zmieni się wartość obu zmiennych?

Niestety, problem, który może pojawić się podczas pomiaru korelacji między dwiema zmiennymi, nazywa się ograniczeniem zakresu . Dzieje się tak, gdy zakres mierzonych wartości dla jednej ze zmiennych jest z jakiegoś powodu ograniczony.

Załóżmy na przykład, że chcemy zmierzyć korelację między godzinami nauki a wynikami uczniów z egzaminów w określonej szkole.

Jeśli zbierzemy dane dotyczące tych dwóch zmiennych dla wszystkich 1000 uczniów w szkole, możemy odkryć, że korelacja między przepracowanymi godzinami a wynikami egzaminów wynosi 0,73 .

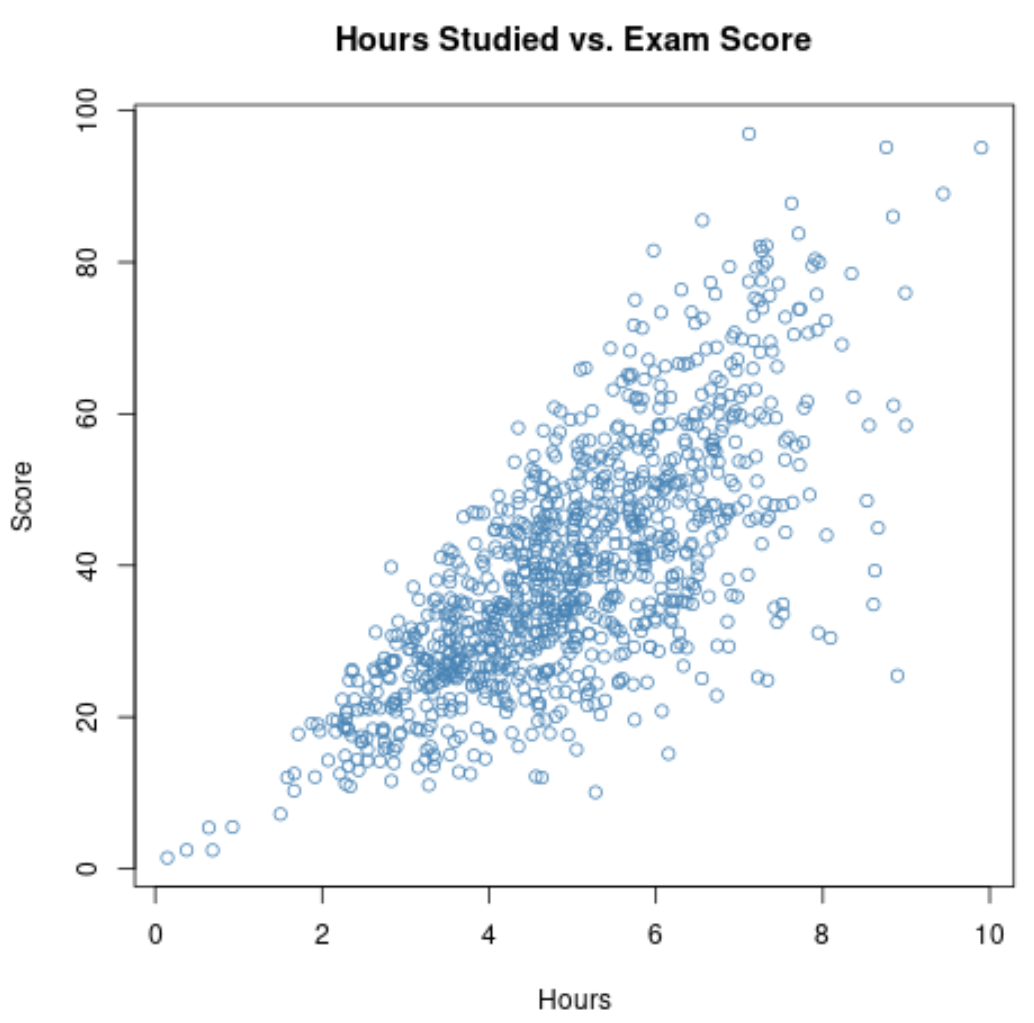
Korelacja ta jest dość wysoka, co wskazuje na silną pozytywną zależność pomiędzy obiema zmiennymi. W miarę jak uczniowie więcej się uczą, zwykle osiągają lepsze wyniki na egzaminach.

Załóżmy jednak, że zbieramy dane tylko o studentach, którzy ukończyli studia z wyróżnieniem. Możliwe, że wszyscy ci uczniowie uczyli się przez co najmniej 6 godzin.

Jeśli więc obliczymy korelację między przestudiowanymi godzinami a wynikami egzaminów dla tych uczniów, użyjemy wąskiego zakresu dla zmiennych godzin przestudiowanych .

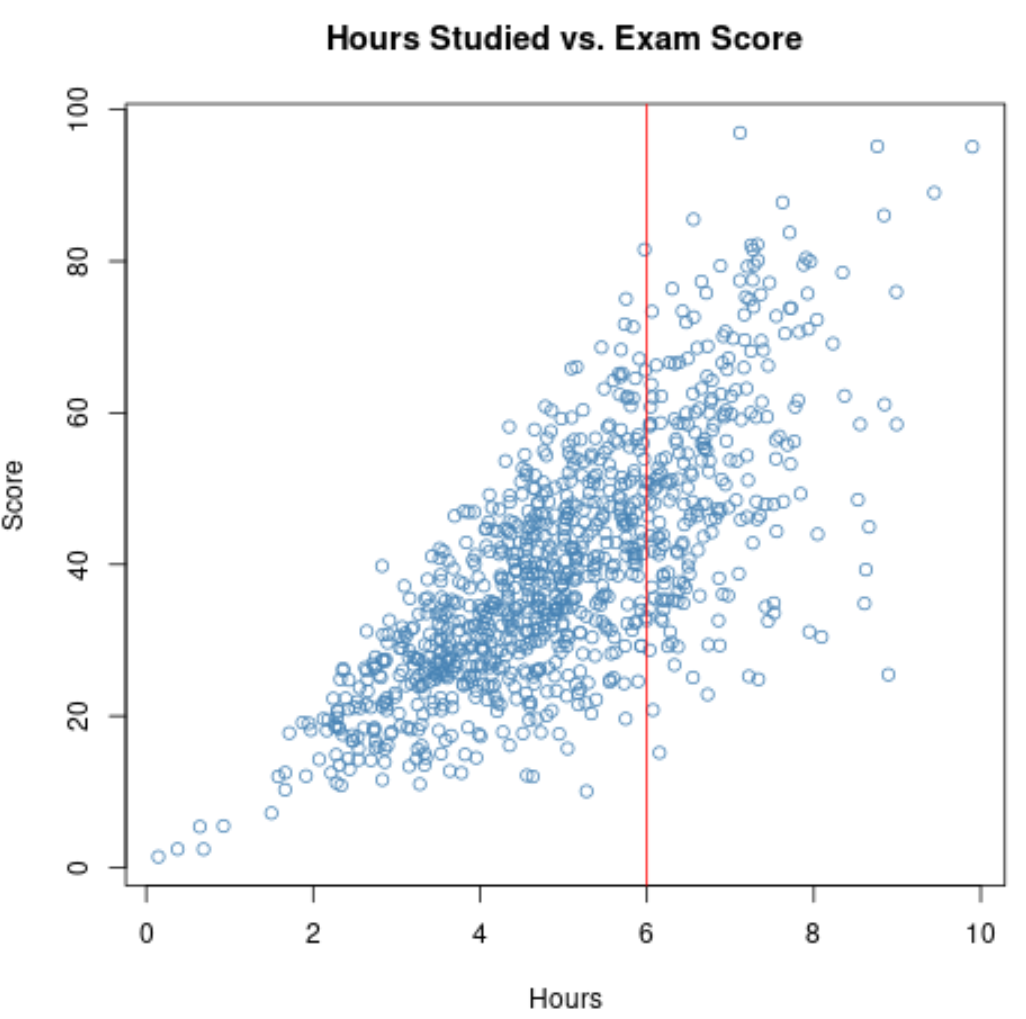
Jeśli powiększymy wykres rozrzutu dla zakresu, w którym godziny są większe niż 6, wykres będzie wyglądał następująco:

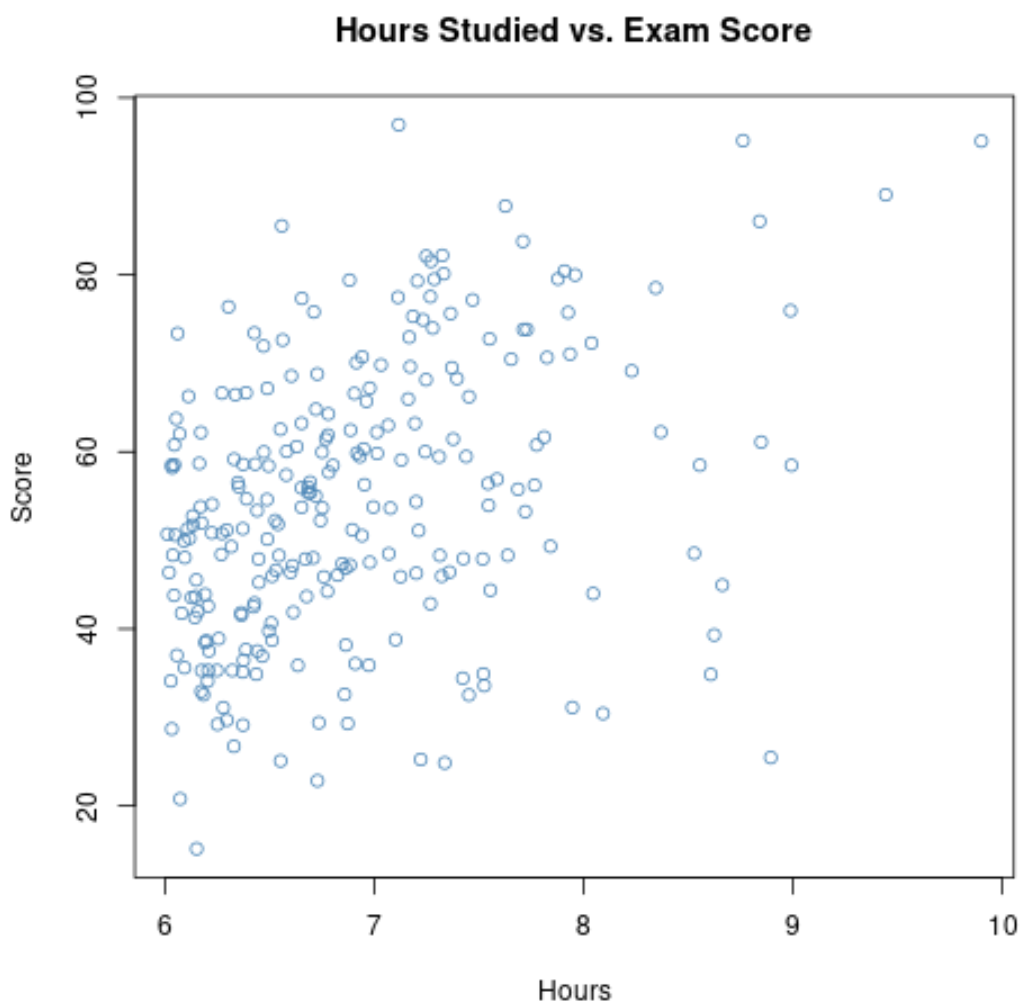
Korelacja między dwiema zmiennymi na tym wykresie okazuje się wynosić 0,37 , czyli znacznie mniej niż 0,73 .

Zatem gdybyśmy zebrali jedynie dane dotyczące godzin przepracowanych i wyników egzaminów uczniów w ramach kursów z wyróżnieniem, moglibyśmy założyć, że istnieje słaby związek między przepracowanymi godzinami a wynikami egzaminów.

Wynik ten byłby jednak mylący, ponieważ dla jednej ze zmiennych zastosowaliśmy ograniczony zakres .

Rzeczywiste przykłady ograniczonego zasięgu

Problem ograniczonego zasięgu może pojawić się w praktyce w wielu różnych badaniach naukowych. Oto kilka przykładów:

1. Badania na sportowcach wyczynowych . Naukowcy mogą być zainteresowani zbadaniem, czy określony program treningowy pozwala uzyskać większą masę mięśniową niż określony program standardowy.

Jeśli badacze zbiorą dane tylko na temat najlepszych sportowców, jest prawdopodobne, że wszyscy ci sportowcy mają już dużą masę mięśniową. Dostępny będzie zatem wąski zakres wartości pozwalających obliczyć korelację pomiędzy programem treningowym a wytworzoną masą mięśniową.

2. Badania uczniów osiągających wysokie wyniki. Naukowcy mogą chcieć zbadać, czy określony program korepetycji ma pozytywny wpływ na oceny. Z natury uczniowie, którzy chcą poprawić swoje oceny i wziąć udział w programie korepetycji, mogą już osiągać wysokie wyniki.

Zatem może nie być zbyt wiele miejsca na poprawę ocen tych uczniów. Kiedy badacze obliczają korelację między godzinami spędzonymi w programie korepetycji a wynikającą z tego poprawą ocen, prawdziwa korelacja może zostać niedoszacowana, ponieważ możliwości poprawy ocen są ograniczone.

Jak uwzględnić ograniczone zakresy

Popularnym sposobem uwzględnienia ograniczonych zakresów jest wzór Thorndike’a 2 opracowany przez psychometra Roberta L. Thorndike’a.

Wzór ten pozwala oszacować prawdziwą korelację między dwiema zmiennymi i wykorzystuje następujące obliczenia:

Prawdziwa korelacja = √(1-(SD ² _{lata ograniczone} – SD ² _{lata nieograniczone} )) * (1-r ² _ograniczone )

Złoto:

• SD ² _{ograniczone y} : Kwadrat odchylenia standardowego dostępnych danych dotyczących zmiennej odpowiedzi y.
• _{Nieograniczone} SD ² y: Znane kwadratowe odchylenie standardowe zmiennej odpowiedzi dla populacji.
• r ² _ograniczone : Korelacja kwadratowa dostępnych ograniczonych danych.

Wykazano, że wzór ten jest skuteczny w tworzeniu bezstronnych szacunków prawdziwej korelacji między dwiema zmiennymi, gdy jedna ze zmiennych ma ograniczony zakres.

Należy pamiętać, że aby skorzystać z tego wzoru, należy oszacować rzeczywiste odchylenie standardowe populacji dla zmiennej odpowiedzi.