Pisanie na maszynie

Przez Benjamin Anderson 5 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, co oznacza scharakteryzowanie rozkładu w statystyce. W ten sposób znajdziesz definicję typizacji, przykład typizacji zmiennej, a dodatkowo będziesz mógł poćwiczyć z rozwiązanym krok po kroku ćwiczeniem.

Co to jest pisanie?

W statystyce normalizacja to proces, w którym do rozkładu stosuje się transformację liniową w taki sposób, że jego średnia i odchylenie standardowe są równe odpowiednio zero i jeden.

Dokładniej, wpisywanie polega na odjęciu średniej od zmiennej losowej, a następnie podzieleniu jej przez odchylenie standardowe.

Wpisywanie można również nazwać normalizacją lub standaryzacją.

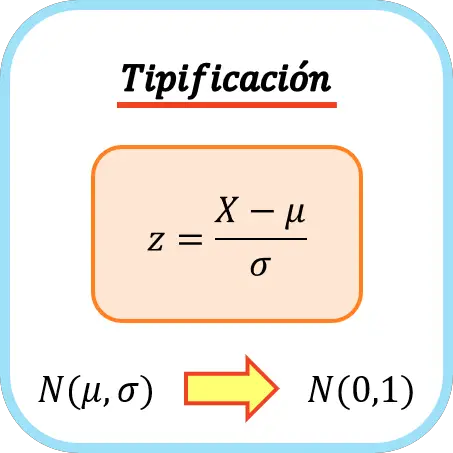
Wprowadź formułę

Aby sklasyfikować zmienną, należy odjąć jej średnią, a następnie podzielić ją przez jej odchylenie standardowe. Wzór na wprowadzenie zmiennej jest zatem następujący:

Złoto

$\mu$

jest średnią zmiennej

$X$

$\sigma$

jego odchylenie standardowe (lub odchylenie standardowe).

Dlatego wpis jest w rzeczywistości zmianą zmiennej, ponieważ do zmiennej stosowana jest transformacja liniowa.

Przykładowy wpis

Biorąc pod uwagę definicję typizacji i jej formułę, poniżej znajduje się konkretny przykład pozwalający w pełni zrozumieć tę koncepcję.

Ciągła zmienna losowa ma rozkład normalny ze średnią 45 i odchyleniem standardowym 10. Jakie jest prawdopodobieństwo otrzymania wartości mniejszej lub równej 60?

$N(45,10)$

Aby znaleźć prawdopodobieństwo rozkładu normalnego, musimy skorzystać z jego tablicy charakterystycznej, ale w tym celu musimy najpierw wykonać proces typowania. Odejmujemy więc średnią i dzielimy przez odchylenie standardowe do wartości prawdopodobieństwa:

$\displaystyle P(X\leq 60)=P\left(Z\leq\frac{60-45}{10}\right)=P(Z\leq 1,5)$

Po standaryzacji przechodzimy do tabeli prawdopodobieństwa rozkładu normalnego, aby sprawdzić, jakiemu prawdopodobieństwu odpowiada wartość 1,5:

Jak widać z tabeli typizacji rozkładu normalnego, wartość obliczona w poprzednim kroku odpowiada prawdopodobieństwu:

$\displaystyle P(Z\leq 1,5)=0,9332$

Prawdopodobieństwo uzyskania wartości równej lub mniejszej od 60 wynosi zatem 93,32%.

Ćwiczenie z pisania rozwiązane

Oblicz następujące prawdopodobieństwa rozkładu normalnego, którego średnia i odchylenie standardowe wynoszą odpowiednio 120 i 50.

$N(120,50)$

Prawdopodobieństwo uzyskania wartości mniejszej lub równej 208.
Prawdopodobieństwo uzyskania wartości większej niż 137.

Zobacz rozwiązanie

W obu częściach problemu musimy wpisać rozkład normalny, aby obliczyć prawdopodobieństwa.

Zaczynamy od obliczenia prawdopodobieństwa wpisania wartości mniejszej lub równej 208:

$\displaystyle P(X\leq 208)=P\left(Z\leq\frac{208-120}{50}\right)=P(Z\leq 1,76)$

A teraz spójrzmy na powyższą tabelę, jakiemu prawdopodobieństwu odpowiada wartość 1,76:

$\displaystyle P(Z\leq 1,76)=0,9608$

Po drugie obliczymy prawdopodobieństwo uzyskania wartości większej niż 137. W ten sam sposób zaczynamy od wpisania zmiennej:

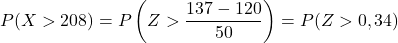$\displaystyle P(X> 208)=P\left(Z>\frac{137-120}{50}\right)=P(Z>0,34)” title=”Rendered by QuickLaTeX.com” height=”43″ width=”398″ style=”vertical-align: -17px;”> <p class=$ Jednak załączona tabela ma tylko najniższe skumulowane prawdopodobieństwa, więc aby skorzystać z tabeli, musimy najpierw przekształcić prawdopodobieństwo:

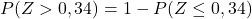$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)” title=”Rendered by QuickLaTeX.com” height=”19″ width=”252″ style=”vertical-align: -5px;”> <p class=$ I na koniec z załączonej tabeli odnotujemy prawdopodobieństwo odpowiadające obliczonej wartości Z:

$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)=1-0,6331=0,3669″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”435″ style=”vertical-align: -5px;”> <div class=$

Jaki jest sens pisania?

Aby dokończyć zrozumienie znaczenia typizacji, zobaczymy do czego służy i kiedy należy wpisać zmienną.

Standaryzacja służy głównie do porównywania wartości rozkładów o różnych średnich i wariancjach. Podobnie standaryzacja jest również wykorzystywana do obliczania prawdopodobieństwa.

Standaryzując dwie wartości rozkładów o różnych charakterystykach, możemy zobaczyć, która wartość jest większa, a która mniejsza w stosunku do całego rozkładu. Innymi słowy, stosując proces typizacji, możemy zobaczyć, która wartość jest najbliższa, a która najdalsza od średniej jej rozkładu.

Dodatkowo, jak wyjaśniono powyżej, typizacja umożliwia również obliczenie prawdopodobieństw, ponieważ generalnie tabele prawdopodobieństwa opierają się na typizowanym rozkładzie.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej